Chapitres Maths en ECS2
Exercices : Algèbre bilinéaire en ECS2
Résumé de cours Exercices Corrigés
Cours en ligne de Maths en ECS2
Exercices : Produit Scalaire, matrices commutantes et base orthonormée
Exercice 1 : Calcul de 
Si ![]() et
et ![]() sont deux éléments de
sont deux éléments de ![]() , on pose:
, on pose:
![]() =
= ![]()
Question 1 :
Montrer que ![]() est une forme bilinéaire sur
est une forme bilinéaire sur ![]() et trouver sa matrice
et trouver sa matrice ![]() dans la base canonique de
dans la base canonique de ![]() .
.
Question 2 :
Est-ce que ![]() est symétrique?
est symétrique?
Question 3 :
Est-ce que ![]() est un produit scalaire ?
est un produit scalaire ?
Question 4 :
![]() est l’endomorphisme de
est l’endomorphisme de ![]() dont la matrice est
dont la matrice est 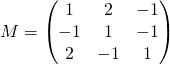 .
.
On pose, pour ![]() ,
, ![]() , dans
, dans ![]() ,
, ![]() .
.
Montrer que ![]() est une forme bilinéaire sur
est une forme bilinéaire sur ![]() et en donner la matrice.
et en donner la matrice.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Exercice 2 : Produit scalaire
![]() ,
, ![]() , est muni de la base canonique
, est muni de la base canonique ![]() , et
, et ![]() est une application continue.
est une application continue.
On définit l’application ![]() par:
par:
![]() est bilinéaire, et, pour tous
est bilinéaire, et, pour tous ![]() de
de ![]() ,
, ![]() .
.
Question 1 :
Question 2 :
Montrer que ![]() est un produit scalaire.
est un produit scalaire.
Exercice 3 : Calcul de produit scalaire
![]() est l’ensemble des applications
est l’ensemble des applications ![]() continues sur
continues sur ![]() , telles que l’intégrale
, telles que l’intégrale
![]() converge.
converge.
Question 1 :
Montrer que ![]() est un espace vectoriel sur
est un espace vectoriel sur ![]() .
.
Question 2 :
Montrer que pour tout ![]() de
de ![]() , la fonction
, la fonction ![]() qui à tout
qui à tout ![]() associe
associe ![]() , appartient à
, appartient à ![]() .
.
Question 3 :
On pose, pour ![]() ,
, ![]() dans
dans ![]() ,
, ![]() .
.
Montrer que ![]() est un produit scalaire sur
est un produit scalaire sur ![]() .
.
Question 4 :
Calculer, pour tous ![]() ,
, ![]() de
de ![]() ,
, ![]() .
.
Exercice 4 : Matrices commutantes
Pour ![]() , on désigne par
, on désigne par ![]() l’espace vectoriel
l’espace vectoriel ![]() des polynômes à coefficients réels de degré inférieur ou égal à
des polynômes à coefficients réels de degré inférieur ou égal à ![]() .
.
On donne ![]() réels
réels ![]() , non nécessairement distincts, et pour
, non nécessairement distincts, et pour ![]() ,
, ![]() appartenant à
appartenant à ![]() , on pose
, on pose
![]() =
=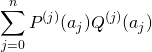 .
.
Question 1 :
Montrer que ![]() est un produit scalaire sur
est un produit scalaire sur ![]() .
.
Question 2 :
On prend dans la suite de l’exercice ![]() .
.
La famille ![]() est-elle orthogonale pour ce produit scalaire?
est-elle orthogonale pour ce produit scalaire?
Question 3 :
Donner une base de ![]() orthonormée pour ce produit scalaire, et les coordonnées d’un polynôme
orthonormée pour ce produit scalaire, et les coordonnées d’un polynôme ![]() de
de ![]() dans cette base.
dans cette base.
Ce résultat était-il prévisible?
Exercice 5 : Base orthonormée de 
Pour ![]() et
et ![]() appartenant à
appartenant à ![]() , on pose:
, on pose:
![]()
=![]()
+![]()
Question 1 :
Montrer que ![]() est un produit scalaire sur
est un produit scalaire sur ![]() .
.
Question 2 :
On notera ![]()
La base canonique de ![]() est-elle orthogonale pour ce produit scalaire?
est-elle orthogonale pour ce produit scalaire?
Construire une base orthonormée de ![]() pour ce produit scalaire.
pour ce produit scalaire.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Exercice 6 : Existence d’un produit scalaire
![]() est muni de la base canonique
est muni de la base canonique ![]() . On définit
. On définit ![]() par:
par:
![]() =
=![]() ,
,
![]() =
=![]() ,
,
![]() =
=![]() .
.
Question 1 :
Montrer que ![]() est une base de
est une base de ![]() . Trouver la matrice de passage
. Trouver la matrice de passage ![]() de
de ![]() à
à ![]() .
.
Question 2 :
Montrer qu’il existe un unique produit scalaire ![]() sur
sur ![]() tel que
tel que ![]() soit une base orthonormée pour ce produit scalaire.
soit une base orthonormée pour ce produit scalaire.
Exercice 7 : Suites et inégalité de Cauchy-Schwarz
Question 1 :
On donne deux suites réelles ![]() et
et ![]() . Montrer que, pour tout
. Montrer que, pour tout ![]() de
de ![]() ,
,
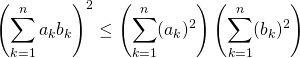 .
.
Question 2 :
Trouver toutes les suites réelles ![]() telles que, pour tout
telles que, pour tout ![]() de
de ![]() ,
,
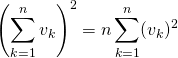 .
.
Exercice 8 : Propriétés d’un espace vectoriel muni d’un produit scalaire
![]() est un espace vectoriel muni d’un produit scalaire.
est un espace vectoriel muni d’un produit scalaire.
Question 1 :
![]() et
et ![]() sont deux parties de
sont deux parties de ![]() . Montrer que
. Montrer que ![]() .
.
Question 2 :
![]() et
et ![]() sont deux sous-espaces vectoriels de
sont deux sous-espaces vectoriels de ![]() . Montrer que
. Montrer que ![]() .
.
Le programme de maths en ECS2 est relativement dense, révisez donc régulièrement les chapitres du programme grâce aux cours en ligne :

