Cours en ligne Physique en Maths Sup
Chapitres Physique en MPSI, PCSI, MP2I, PTSI
Exercices corrigés sur l’électricité (perm./transitoire) en maths sup
Résumé de cours Exercices et corrigés
Cours en ligne de physique en Maths Sup
L’étude de l’électricité, notamment ses aspects permanents et transitoires, représente un domaine crucial dans les programmes de maths sup, offrant une compréhension approfondie des phénomènes électriques fondamentaux et de leurs applications pratiques. Si vous rencontrez des difficultés dans cette matière, envisagez de recourir à des cours particuliers en physique chimie. Nous nous efforçons d’adapter les expériences d’apprentissage à vos besoins individuels, et vos intérêts et à votre rythme. Vous bénéficierez ainsi d’une approche individualisée qui vous aidera à surmonter vos difficultés spécifiques en électricité.
Exercices corrigés : Lois de Kirchhof
Plan des exercices sur l’électricité (perm./transitoire) :
A. Lois de Kirchhoff
B. Résistors
C. Bobines et condensateurs
D. Circuits RC, RL, LC
COURS PARTICULIERS DE PHYSIQUE
Nous avons recruté pour vous les meilleurs profs de physique.
POUR M'AMÉLIORER EN PHYSIQUE, JE CHERCHE DES
Avis Google France ★★★★★ 4,9 sur 5
A. Lois de Kirchhoff
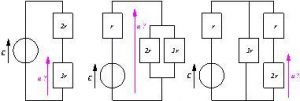
Ex. 1. Circuit complexe.
Dans le circuit suivant, les dipôles représentés par des rectangles sont tous identiques, mais on ne connaît pas leur nature.
On donne
![]() ,
, ![]() ,
, ![]() ,
, ![]() et
et ![]() .
.
1. Déterminer toutes les intensités du circuit.
2. Déterminer la tension aux bornes de chaque dipôle.
3. Déterminer le potentiel de chaque point.
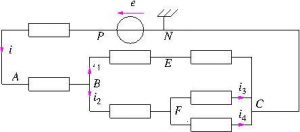
Correction :
1. Les deux branches étant identiques![]() .
.
En appliquant la loi des nœuds![]()
et ![]() .
.
2. Les deux dipôles identiques étant parcourus par la même intensité, ![]()
En appliquant la loi d’additivité des tensions ![]()
donc ![]() .
.
De plus, ![]()
donc ![]() et
et ![]()
De même, ![]()
et ![]()
donc ![]() .
.
3. Par définition de la masse ![]()
puis on remonte les potentiels![]() donc
donc ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() et
et ![]()
Ex. 2. Conservation de la puissance.
Un circuit comporte une maille unique formée d’un dipôle générateur ![]() et de
et de ![]() dipôles récepteurs.
dipôles récepteurs.
On note ![]() la tension aux bornes du générateur,
la tension aux bornes du générateur,
![]() celle aux bornes du
celle aux bornes du ![]() -ième récepteur,
-ième récepteur,
![]() l’intensité du courant qui le traverse
l’intensité du courant qui le traverse
et ![]() la puissance qu’il reçoit.
la puissance qu’il reçoit.
Montrer que ![]() .
.
B. Résistors
Ex. 1. Losange.
Donner la résistance équivalente de l’association suivante.
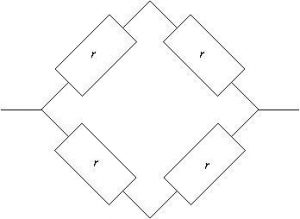
Correction :
![]()
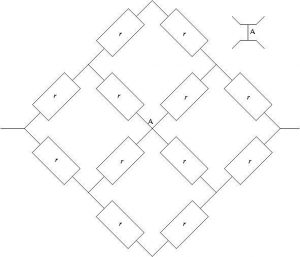
Ex. 2. Double losange.
Dans le montage suivant, on fait un zoom sur le nœud A en haut de la figure.
1. Justifier qu’on peut couper le fil vertical au niveau du nœud A zoomé.
2. En déduire la résistance équivalente du montage.
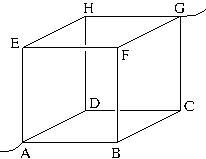
Ex. 3. Résistance d’un cube.
Dans le circuit suivant, chacune des 12 arêtes du cube a une résistance ![]() .
.
Déterminer la résistance équivalente entre les deux fils, en A et en G.
Ex. 4. Diviseurs de tension.
Dans les trois circuits suivants, déterminer ![]() .
.
COURS DE PHYSIQUE-CHIMIE
Nous avons sélectionné pour vous les meilleurs profs particuliers.
POUR ACCÉLÉRER MA PROGRESSION EN PHYSIQUE-CHIMIE, JE TROUVE DES
Avis Google France ★★★★★ 4,9 sur 5
C. Bobines et condensateurs
Ex. 1. Loi d’association de bobines en série.
Quelle est l’inductance équivalente de trois bobines en série ![]() ,
, ![]() et
et ![]() ?
?
Correction :
L’intensité qui traverse les bobines est la même donc ![]()
![]()
![]()
donc ![]()
Ex. 2. Loi d’association de condensateurs en parallèle.
Quelle est la capacité équivalente de trois condensateurs en parallèle ![]() ,
, ![]() et
et ![]() ?
?
Ex. 3. Analyse qualitative d’un circuit.
1. Préliminaire. En régime permanent, quelle est l’intensité traversant un condensateur ? la tension aux bornes d’une bobine ?
2. Application. Dans le circuit suivant, les lampes sont assimilées à des résistors de résistance ![]()
À la date ![]() , on ferme l’interrupteur K.
, on ferme l’interrupteur K.
Décrire qualitativement l’évolution de la brillance des deux lampes, en admettant qu’elle est proportionnelle au carré
de l’intensité du courant qui les traverse. On pourra se limiter à donner l’état juste après la fermeture de K, et longtemps après.
![]()
![]() À la date
À la date ![]() , on ferme l’interrupteur K. Décrire qualitativement l’évolution de la brillance des deux lampes, en admettant qu’elle est proportionnelle au carré de l’intensité du courant qui les traverse. On pourra se limiter à donner l’état juste après la fermeture de K, et longtemps après. » width= »276″ height= »238″ />
, on ferme l’interrupteur K. Décrire qualitativement l’évolution de la brillance des deux lampes, en admettant qu’elle est proportionnelle au carré de l’intensité du courant qui les traverse. On pourra se limiter à donner l’état juste après la fermeture de K, et longtemps après. » width= »276″ height= »238″ />
D. Circuits RC, RL, LC
Ex. 1. Bilan énergétique RC.
Un générateur de tension ![]() alimente une association série RC avec
alimente une association série RC avec ![]() et
et ![]()
1. Établir les expressions de ![]() aux bornes du condensateur (sa tension initiale est nulle) et
aux bornes du condensateur (sa tension initiale est nulle) et ![]() dans le circuit.
dans le circuit.
2. Faire un bilan énergétique pour ![]() en calculant l’énergie fournie par le générateur, celle emmagasinée par le condensateur et celle dissipée par effet joule dans le résistor.
en calculant l’énergie fournie par le générateur, celle emmagasinée par le condensateur et celle dissipée par effet joule dans le résistor.
Ex. 2. Circuit CRC
Un circuit est formé de deux condensateurs de même capacité ![]() reliés en série avec un résistor de résistance
reliés en série avec un résistor de résistance ![]()
À ![]() , la tension du condensateur 1 vaut
, la tension du condensateur 1 vaut ![]() et celle du condensateur 2 est nulle
et celle du condensateur 2 est nulle ![]()
1. Établir le système d’équations différentielles vérifiées par ![]() et
et ![]()
2. Résoudre le système.

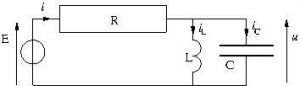
Ex. 3. Circuit RLC parallèle.
Un générateur de tension alimente l’association série d’une résistance ![]() et de l’association parallèle LC.
et de l’association parallèle LC.
On définit le facteur de qualité
![]()
1. Établir l’équation différentielle vérifiée par ![]() , tension aux bornes du condensateur (donc égale à celle aux bornes de la bobine).
, tension aux bornes du condensateur (donc égale à celle aux bornes de la bobine).
2. Donner les CI ![]() et
et ![]()
3. À quelle condition sur ![]() observe-t-on des oscillations électriques ?
observe-t-on des oscillations électriques ?
Pourquoi ne pas prendre de l’avance sur vos camarades en commençant dès maintenant à réviser et à vous tester sur les chapitres qui suivent :

