Cours en ligne Physique en Maths Sup

Chapitres Physique en MPSI, PCSI, MP2I, PTSI

Exercices corrigés sur l’optique géométrique en maths sup

Name: Groupe Réussite: Cours particuliers, stages intensifs de révision
Brand: Groupe Réussite
SKU: Cours Particuliers
Rating: 4.9 (1049 reviews)

Résumé de cours Exercices corrigés

Cours en ligne de physique en Maths Sup

L’étude de l’optique géométrique représente un pilier fondamental dans les programmes des classes préparatoires aux grandes écoles scientifiques, maths sup, offrant une approche cruciale pour comprendre le comportement de la lumière et ses applications pratiques en physique. Il est vivement conseillé de prendre un professeur particulier en physique chimie pour bénéficier d’un soutien adapté à vos besoins spécifiques. En choisissant nos services, vous avez l’assurance d’avoir un enseignant compétent qui connaît le programme et sait comment vous préparer efficacement.

A. Exercices lois de Descartes en MPSI, MP2I, PCSI et PTSI

Ex. 1. Mirage thermique.

La température de l’air dans le désert varie avec l’altitude $z$ . L’indice de réfraction varie selon une loi du type
$\displaystyle{n(z)=n_0\sqrt{1-\frac{z^2}{z_0^2}}}$
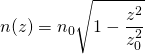
Un rayon lumineux est émis depuis le point $O(0,0)$ avec un angle $i_0$ mesuré par rapport à la verticale.

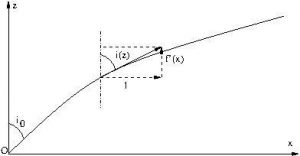
1. Justifier la concavité de la trajectoire du rayon lumineux.

2. Jusqu’à quelle altitude le rayon monte-t-il ? Que se passe-t-il ensuite ?

Correction :

1. Il y a conservation de l’invariant de Descartes :
$n(z)\sin i(z)=n_0\sin i_0$
Or $n$ est une fonction décroissante de $z$ , donc $i$ est une fonction croissante de $z$ , la tangente est donc de plus en plus horizontale, la courbe est donc concave.
2. $i(z)$ est défini tant que
$\displaystyle{\frac{n_0}{n(z)}\sin i_0\leq 1}$
soit $\displaystyle{\frac{z^2}{z_0^2}\leq 1-\sin^2i_0=\cos^2i_0}$
soit $z\leq z_0\cos i_0$
À cette altitude, il y a réflexion totale et le rayon repart vers le bas, ce qui forme le mirage optique.

COURS PARTICULIERS DE PHYSIQUE

Nous avons recruté pour vous les meilleurs profs de physique.

POUR M'AMÉLIORER EN PHYSIQUE, JE CHERCHE DES

Avis Google France ★★★★★ 4,9 sur 5

Ex. 2. Effet miroir dans un aquarium.

Un aquarium est assimilé à un parallélépipède rectangle rempli d’eau d’indice $n=1,5$ et placé dans l’air d’indice $1$ .
On se place en face et on essaye de regarder à travers la vitre de côté (voir schéma).
Déterminer la marche du rayon entrant et expliquer pourquoi on a l’impression que la vitre de côté se comporte comme un miroir.

Ex. 3. Opacité d’un tube rempli de mercure.

Un thermomètre à mercure est formé d’un tube cylindrique creux en verre d’indice $n$ , de rayons intérieur $r$ et extérieur $R$ , il est au contact de l’air d’indice $1$ et rempli de mercure (liquide opaque réfléchissant).
En vous inspirant du rayon tracé, déterminer la valeur minimale de $\frac{r}{R}$ pour laquelle un observateur a l’impression que le cylindre est complètement en mercure.

Ex. 4. Déviation dans une goutte d’eau.

Une goutte d’eau sphérique, d’indice $n$ , de centre $O$ , est frappée en $A$ par un rayon lumineux avec un angle d’incidence $i$ . Il se réfléchit à l’intérieur de la goutte en B et en ressort en C. L’angle de déviation D est l’angle entre le rayon entrant et le rayon sortant.
Exprimer $D$ en fonction de $i$ et de $r$ en précisant la relation entre $i$ et $r$ .

Ex. 5. Fibre optique à saut d’indice.

Une fibre optique de longueur $L$ , dite << à saut d’indice >> est constituée d’une âme cylindrique transparente et d’indice $n$ , entourée par une gaine elle aussi cylindrique d’indice $n'\leq n$ .

Un rayon laser, se propageant dans l’air d’indice 1, frappe le bord gauche de la fibre en E, au niveau de l’axe, avec un angle d’incidence $\alpha$ .
Il entre dans la fibre avec un angle réfracté $\beta$ .
Il frappe alors le dioptre entre les deux milieux en F.

On suppose qu’il y a réflexion totale en $F$ . Le rayon se propage ainsi le long de la fibre selon une ligne brisée et en sortira en S.

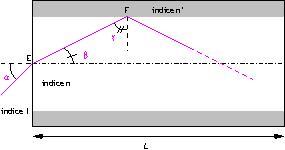
1. Déterminer la valeur maximale $\alpha_2$ de $\alpha$ assurant la réflexion totale en $F$

2. Exprimer la durée $\tau_1$ de traversée de la fibre avec $\alpha=0$ et la durée $\tau_2$ avec $\alpha=\alpha_2$

3. Le signal envoyé par la fibre optique est une succession de très courtes impulsions longues ou brèves (bits) émis toutes les $T$ secondes, avec une fréquence $f=\frac1T$

Le message sera transmis avec succès si l’ordre dans lequel les impulsions sont reçues est rigoureusement le même que celui dans lequel elles ont été émises.
En déduire la valeur minimale de $T$ et la fréquence maximale $f$ exprimée en bits par seconde.

COURS DE PHYSIQUE-CHIMIE

Nous avons sélectionné pour vous les meilleurs profs particuliers.

POUR ACCÉLÉRER MA PROGRESSION EN PHYSIQUE-CHIMIE, JE TROUVE DES

Avis Google France ★★★★★ 4,9 sur 5

B. miroirs plans et lentilles

Ex. 1. Se mirer.

Un individu de hauteur $H$ veut se voir de pied en cap dans un miroir plan fixé au mur vertical en face de lui. Quelle est la hauteur minimale $h$ du miroir ?

Correction :

On note P la position de ses pieds, Y celle de ses yeux et S le sommet de sa tête. Il faut que l’individu voit son image $P'S'$ qui est le symétrique orthogonal de $PS$ par rapport au mur.
Un schéma suffit à conclure.
On trace le rayon S’Y et le rayon P’Y.
On délimite ainsi le haut T et le bas B du miroir en prenant les intersections de S’Y avec le mur (T) et de P’Y avec le mur (B).
L’application du théorème de Thalès permet d’en déduire que la hauteur du miroir $h=BT$ est égal à la moitié de la hauteur de l’individu :
$h=H/2$

Ex. 2. Catadioptre à deux dimensions.

Deux miroirs sont à angle droit dans un coin de mur. On travaille dans un plan d’altitude constante $H$ . Soir A un point de la pièce à l’altitude $H$ .

Montrer que tout rayon issu de A et se déplaçant dans le plan de travail ressort, après réflexion(s) sur le(s) miroir(s), parallèle au rayon incident.

Ex. 3. Calcul de grandissement.

Quel est le grandissement d’un objet AB placé à 13 cm à gauche d’une lentille CV de vergence $V=+8~\delta$

Ex. 4. Détermination des caractéristiques d’une lentille.

Une lentille donne l’image réelle A’B’ de l’objet réel AB.
On connaît la distance $AA'=120~\mathrm{cm}$ et les tailles $\overline{AB}=12~\mathrm{mm}$ et $\overline{A'B'}=-36~\mathrm{mm}$

Déterminer la position et la vergence de la lentille.

Ex. 5. Focométrie de Bessel.

Soit une lentille L convergente mais de distance focale $f'$ inconnue.
On place, sur un banc d’optique, un objet AB et un écran E à la distance $D$ suffisamment grande de l’objet. On définit un axe $(O,x)$ tel que $x_A=0$ et $x_E=D$ .
On place L entre l’objet et l’écran, et on la déplace.
Pour deux abscisses $x_1$ et $x_2$ de la lentille avec $x_1 < x_2$ on observe une image nette sur l’écran. On pose $d=x_2-x_1$ .

1. Établir l’équation vérifiée par $x$ lorsqu’on observe une image nette sur l’écran.
2. En déduire $f'$ en fonction de $d$ et de $D$ .
3. Que signifie la locution << $D$ suffisamment grande>> de l’énoncé ?

C. Instruments d’optique

Ex. 1. Objet virtuel ?

Dans quelle situation concrète parle-t-on d’objet virtuel ?

Correction :

Dans une association de lentilles, lorsque l’image $A_1B_1$ de l’objet $AB$ par la première lentille se forme à droite de la seconde, $A_1B_1$ est une image réelle par $L_1$ et un objet virtuel pour $L_2$ .

Ex.2. Lunette astronomique.

Une lunette astronomique est formée de l’association de deux lentilles.

L’objectif $L_1$ est une lentille convergente de distance focale $f'_1=1,00~\mathrm{m}$ et de centre $O_1$
l’oculaire $L_2$ est une lentille divergente de distance focale $f'_2=-12,5~\mathrm{cm}$ et de centre $O_2$
1. Donner la distance $\overline{O_1O_2}$ pour que la lunette soit afocale.
2. Deux faisceaux venant de deux étoiles $A_{\infty}$ sur l’axe du système optique

et $B_{\infty}$ frappent l’objectif au voisinage de $O_1$ sous un angle $\theta$ .

Construire les images $A_1$ et $B_1$ par l’objectif puis les faisceaux émergeant du système sous un angle $\theta'$ .
3. Déterminer le grossissement $G=\frac{\theta'}{\theta}$ (on est dans les conditions de Gauss donc on peut faire l’approximation des petits angles.

Ex. 3. Microscope.

Un microscope est formé de l’association de deux lentilles

L’objectif $L_1$ est une lentille convergente de distance focale $f'_1=5,00~\mathrm{mm}$

l’oculaire $L_2$ est une lentille convergente de distance focale $f'_2=25,0~\mathrm{mm}$
et la distance entre les deux lentilles est définie par
$F'_1F_2=25,0~\mathrm{cm}$ .

On observe une cellule assimilée à un
objet $AB$ de taille $\overline{AB}=+1,0\mu\mathrm{m}$ .

1. Calculer $\overline{O_1A}$ et $\overline{A_1B_1}$

2. Le grossissement commercial $G_c$ . est le rapport entre l’angle $\alpha'$ sous lequel on voit la cellule à travers l’oculaire du microscope

et l’angle $\alpha_0$ sous lequel on verrait la cellule à l’œil nu à une distance de 25 cm. Calculer $G_c$

Utilisez les cours en ligne et leurs exercices corrigés de physique en MPSI, PCSI et PTSI pour maximiser vos révisions et améliorer vos notes en Maths Sup :