Cours en ligne Physique en Maths Sup
Chapitres Physique en MPSI, PCSI, MP2I, PTSI
Exercices corrigés : La superposition en Maths Sup
Résumé de cours Exercices et corrigés
Cours en ligne de physique en Maths Sup
L’étude de la superposition représente un élément fondamental en maths sup, offrant une approche essentielle pour comprendre la physique chimie. Si vous cherchez à approfondir cette notion, prendre des cours particuliers en physique chimie peut s’avérer bénéfique.
La force réside dans la relation de confiance qui se développe entre vous et le professeur et les parents, favorisant ainsi un environnement propice à une progression significative. Cette dynamique encourageante permet un apprentissage plus efficace et une meilleure compréhension des notions clés de la superposition en maths sup.
Exercices : Interférences, Diffraction, Polarisation
Plan des exercices sur les ondes en MPSI, PCSI, PTSI :
A. Interférences
B. Battements (PCSI)
C. Ondes stationnaires
D. Diffraction
E. Polarisation (PCSI)
COURS PARTICULIERS DE PHYSIQUE
Nous avons recruté pour vous les meilleurs profs de physique.
POUR M'AMÉLIORER EN PHYSIQUE, JE CHERCHE DES
Avis Google France ★★★★★ 4,9 sur 5
A. Interférences
Ex. 1. Superposition de deux signaux.
Quelle est l’amplitude et la phase du signal résultant de la superposition des signaux suivants :
a. 
et 
b. 
et 
c. 
et 
Correction :
a. On fait la construction de Fresnel (voir ci-dessous).
On lit l’amplitude 
et la phase 
b. On peut écrire
donc 
d’amplitude 1 et de phase 
c. Les deux signaux n’ont pas la même pulsation, ils n’interfèrent pas.
Ex. 2. Interférences onde-écho.
Un émetteur d’onde sonore est placé en 
L’onde d’amplitude 
et de fréquence 
se propage sur l’axe des 
à la célérité 
Un récepteur est placé en 
d’abscisse 
En 
on place un mur qui réfléchit l’onde. En on reçoit la superposition de l’onde incidente et de l’onde réfléchie.
a. On prend 
. Calculer le déphasage entre les deux ondes.
En déduire l’amplitude du signal en en supposant qu’au rebond sur le mur, l’amplitude est conservée (écho parfait).
b. Même question en supposant que l’amplitude au rebond est divisée par 2.
c. Quelle est la plus petite valeur de 
pour laquelle on a interférences destructives en ?
B. Battements (PCSI)
Ex. 1. Battements acoustiques.
Deux flûtes mal accordées jouent un la de fréquence
moyenne 
. L’une joue légèrement trop aigu, l’autre
légèrement trop grave. On entend distinctement 6 battements par seconde,
c’est-à-dire que l’enveloppe s’annule sept fois par seconde. En déduire
une estimation des fréquences 
et 
.
Correction :
On a deux inconnues, on doit donc écrire deux équations.
Quand on superpose les deux ondes sonores, on a le produit de la porteuse dont la fréquence vaut la fréquence moyenne 
et de l’enveloppe qui s’écrit 
Cette enveloppe s’annule lorsque le cosinus vaut zéro, donc quand 
avec 
entier
donc quand 
donc avec une fréquence 
On résout le système et on trouve
et 
COURS DE PHYSIQUE-CHIMIE
Nous avons sélectionné pour vous les meilleurs profs particuliers.
POUR ACCÉLÉRER MA PROGRESSION EN PHYSIQUE-CHIMIE, JE TROUVE DES
Avis Google France ★★★★★ 4,9 sur 5
C. Ondes stationnaires
Ex. 1. Stroboscopie.
Pour observer en détail une corde de longueur 
, fixée à ses deux extrémités, on l’éclaire avec un stroboscope de fréquence 
, c’est-à-dire qu’il émet un éclair toutes les secondes.
On part d’une valeur très élevée de et on diminue sa valeur progressivement.
Pour la fréquence 
, on observe pour la première fois l’immobilité apparente de la corde sous la forme suivante
a. Comment interpréter l’observation ?
b. Calculer la célérité 
de l’onde le long de la corde.
c. Qu’observe-t-on pour 
?
d. Qu’observe-t-on pour 
?
e. Qu’observe-t-on pour 
?
f. Qu’observe-t-on pour 
?
Correction :
a. Entre deux éclairs, la corde fait exactement une vibration complète, donc sa fréquence de vibration est égale à la fréquence des éclairs donc 
b. En appliquant le résultat du cours, on distingue 
demi-longueurs d’onde (demi-sinusoïdes) donc la relation de quantification s’écrit 
soit 
soit 
c. La durée qui sépare deux éclairs consécutifs est multipliée par 2. La corde fait donc deux vibrations complète et on a immobilité apparente, on observe donc la même figure.
d. La durée qui sépare deux éclairs consécutifs est divisée par 2. La corde ne fait donc qu’une demi-vibration donc on voit (avec la persistance rétinienne) la superposition de deux cordes en opposition de phase (figure d)
e. La durée qui sépare deux éclairs est très légèrement supérieure à la période de vibration. La corde a donc le temps de faire un tout petit peu plus d’une vibration. À chaque éclair, on a donc l’impression qu’elle bouge une tout petit peu. On a donc mouvement apparent ralenti direct (dans le même sens que la vibration).
f. La durée qui sépare deux éclairs est très légèrement inférieure à la période de vibration. La corde a donc le temps de faire un tout petit peu moins d’une vibration. À chaque éclair, on a donc l’impression qu’elle bouge une tout petit peu. On a donc mouvement apparent ralenti rétrograde (dans le sens
inverse à la vibration).
Ex. 2. Harmonique.
Avec un instrument à corde pincée,
comme la guitare, on pince une corde, de longueur 
, avec l’ongle ou un plectre avec une main (la droite en général), et avec l’autre main sur le manche, on pose un doigt sur la corde.
La célérité de l’onde vaut 
Il y a deux manières de poser le doigt.
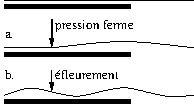
a. On appuie fermement sur la corde et on bloque toute la partie supérieure de la corde un noeud de vibration à cet endroit. La corde est donc une corde fixée à ses deux extrémités, de longueur 
Pourquoi le choix de impose-t-il la fréquence du son émis par la corde, et donc la note ?
(On admettra que le son le plus audible correspond au mode 
).
b. On éfleure la corde et on impose un noeud de vibration à cet endroit mais sans bloquer la partie supérieure de la corde, donc la longueur vibrante reste 
et la distance entre le chevalet et le doigt vaut 
Quelle est la fréquence du son entendu ?
(On prendra la valeur la plus petite compatibe avec les données). Le son entendu s’appelle une harmonique.
D. Diffraction
Ex. 1. Tache de diffraction.
Quand 
est petit (inférieur à 
) on peut identifier 
Un large faisceau de lumière de longueur d’onde 
frappe une cloison opaque percée d’une fenêtre rectangulaire de hauteur 
et de largeur .
a. Dans une direction donnée, l’angle de faisceau est-il petit quand la fenêtre est grande ou petite ?
b. La fenêtre est une fente de largeur 
et de hauteur 
. Calculer l’angle de faisceau horizontal et vertical 
.
c. On place un écran à 
de la cloison. Donner la forme et la taille de la figure observée.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
E. Polarisation (PCSI)
Ex. 1. Changement de l’axe de polarisation.
On considère un faisceau de lumière polarisé rectilignement selon 
et se propageant dans la direction et le sens de 
Est-il possible de le transformer en un faisceau de mêmes direction et sens de propagation, mais d’axe de polarisation selon 
?
Ex. 2. Pouvoir rotatoire.
Un faisceau horizontal de lumière polarisée rectilignement traverse un aquarium rempli d’eau pure ; on mesure l’intensité 
à la sortie de l’aquarium. On place un analyseur à la sortie de l’aquarium. On observe une extinction lorsque l’axe de l’analyseur est vertical.
On dissout du sucre dans l’eau et on constate, sans changer la direction de l’analyseur, qu’il n’y a plus extinction, on détecte une intensité
à sa sortie avec 
.
On tourne alors l’analyseur d’un angle et on retrouve une extinction.
Proposer une explication à ce phénomène et donner la valeur numérique de l’angle dont a tourné l’axe de polarisation de la lumière quand elle a traversé l’aquarium.
Pour être sûr de vos connaissances sur l’ensemble des chapitres qui sont au programme de Maths Sup en physique, testez-vous sur les exercices des cours suivants :