Chapitres Maths en ECG1
Chapitres Maths en ECG1
Cours : Extrema et convexité en ECG1
Résumé de cours Exercices Corrigés
Cours en ligne de Maths en ECG1
Résumé de cours et méthodes – Extrema et convexité
1. Méthodes sur les extrema
Méthode 1 : Montrer qu’une fonction admet un mimimum/un maximum global.
On rappelle le théorème le plus important : soit ![]() une fonction continue sur le segment
une fonction continue sur le segment ![]() Alors
Alors ![]() admet un minimum et un maximum sur
admet un minimum et un maximum sur ![]() Ce résultat ne donne aucune information sur la manière de les trouver…
Ce résultat ne donne aucune information sur la manière de les trouver…
Pour cela, on rappelle le résultat suivant : soit ![]() une fonction dérivable. Si
une fonction dérivable. Si ![]() admet un maximum ou un minimum en
admet un maximum ou un minimum en ![]() alors
alors ![]() (un tel point
(un tel point ![]() s’appelle un point critique). En pratique, on résout l’équation
s’appelle un point critique). En pratique, on résout l’équation ![]() et on vérifie que les solutions trouvées sont (ou pas) des maximums/ des minimums.
et on vérifie que les solutions trouvées sont (ou pas) des maximums/ des minimums.
Piège : Attention la condition ![]() n’est qu’une condition nécessaire pour avoir un extremum (minimum ou maximum), c’est-à-dire que lorsque l’on a un point critique, il n’y a pas forcément de minimum/maximum.
n’est qu’une condition nécessaire pour avoir un extremum (minimum ou maximum), c’est-à-dire que lorsque l’on a un point critique, il n’y a pas forcément de minimum/maximum.
Les méthodes sur l’extrema et convexité peut paraître bloquant pour certains élèves en ECG1, l’aide d’un professeur particulier de maths peut être un atout.
Exemple : Les deux questions sont indépendantes.
1) Soit ![]() continue. Montrer qu’il existe
continue. Montrer qu’il existe ![]() tel que pour tout
tel que pour tout ![]()
![]()
2) Soit ![]() une fonction continue, non constante et admettant
une fonction continue, non constante et admettant ![]() comme limite en
comme limite en ![]() Montrer que
Montrer que ![]() admet un extremum global sur
admet un extremum global sur ![]()
Réponse : 1) ![]() étant continue sur le segment
étant continue sur le segment ![]()
![]() admet un minimum en
admet un minimum en ![]() Si l’on pose
Si l’on pose ![]() alors pour tout
alors pour tout ![]() on a
on a ![]() donc
donc ![]()
2) Il existe ![]() tel que
tel que ![]()
![]() On commence par supposer
On commence par supposer ![]() On traduit la limite de
On traduit la limite de ![]() en
en ![]() en prenant
en prenant ![]()
Il existe ![]() tel que si
tel que si ![]()
![]() Cela donne
Cela donne
![]()
alors ![]()
![]() est continue sur
est continue sur ![]() donc
donc ![]() admet un maximum
admet un maximum ![]() atteint en un point
atteint en un point ![]() Alors
Alors ![]()
Sur ![]()
![]() On a prouvé que
On a prouvé que ![]() admet un maximum égal à
admet un maximum égal à ![]() obtenu en
obtenu en ![]()
![]() Dans le cas où
Dans le cas où ![]() on pose
on pose ![]()
![]() est continue non constante et admet une limite en
est continue non constante et admet une limite en ![]() égale à
égale à ![]() et vérifie
et vérifie ![]() avec
avec ![]()
D’après le premier cas, ![]() admet un maximum global
admet un maximum global ![]() alors
alors ![]() admet un minimum global égal à
admet un minimum global égal à ![]()
Dans les deux cas, on a prouvé que ![]() admet un extremum global atteint en un point de
admet un extremum global atteint en un point de ![]()
Méthode 2 : Manipuler la notion d’extremum local (une condition nécessaire puis une condition suffisante)
Soit ![]() une fonction définie sur un intervalle
une fonction définie sur un intervalle ![]() à valeurs dans
à valeurs dans ![]() On rappelle que
On rappelle que ![]() admet un minimum (respectivement maximum) local en
admet un minimum (respectivement maximum) local en ![]() s’il existe
s’il existe ![]() tel que pour tout
tel que pour tout ![]()
![]() (respectivement
(respectivement ![]() ).
).
Il est évident que si ![]() admet un extremum global en
admet un extremum global en ![]()
![]() admet un extremum local en
admet un extremum local en ![]()
![]() Condition nécessaire : Soit
Condition nécessaire : Soit ![]() un intervalle ouvert, si
un intervalle ouvert, si ![]() est dérivable en
est dérivable en ![]() et si
et si ![]() admet un extremum local en
admet un extremum local en ![]() alors
alors ![]() On dit que le point
On dit que le point ![]() est un point critique de
est un point critique de ![]()
En pratique, on résout l’équation ![]() et on vérifie que les solutions trouvées sont (ou ne sont pas) des extremums locaux (généralement en étudiant les variations de la fonction).
et on vérifie que les solutions trouvées sont (ou ne sont pas) des extremums locaux (généralement en étudiant les variations de la fonction).
![]() Condition suffisante d’extremum local : Soient
Condition suffisante d’extremum local : Soient ![]() un intervalle ouvert,
un intervalle ouvert, ![]() est de classe
est de classe ![]() sur
sur ![]() à valeurs dans
à valeurs dans ![]() et
et ![]() On suppose que
On suppose que ![]() Si
Si ![]() (respectivement
(respectivement ![]() ), alors
), alors ![]() admet en
admet en ![]() un maximum local (respectivement un minimum local).
un maximum local (respectivement un minimum local).
Remarque : ![]() Attention la condition
Attention la condition ![]() n’est pas une condition suffisante pour avoir un extremum local (prendre par exemple
n’est pas une condition suffisante pour avoir un extremum local (prendre par exemple ![]() en
en ![]() ).
).
![]() Si
Si ![]() et
et ![]() on ne peut rien dire ! On peut avoir un maximum ou un minimum local ou bien rien du tout (reprendre l’exemple de
on ne peut rien dire ! On peut avoir un maximum ou un minimum local ou bien rien du tout (reprendre l’exemple de ![]() en
en ![]() ).
).
Exemple : Cet exercice utilise des notions sur les équivalents et les développements limités.
Soit ![]() une fonction de classe
une fonction de classe ![]() sur
sur ![]() et telle que
et telle que ![]() soit
soit ![]() sur
sur ![]() Soit
Soit ![]() tel que
tel que ![]() Montrer que
Montrer que ![]()
Réponse :
Comme ![]() est positive et
est positive et ![]()
![]() admet un minimum global en
admet un minimum global en ![]() donc
donc ![]() écrivons la formule de Taylor-Young pour
écrivons la formule de Taylor-Young pour ![]() à l’ordre
à l’ordre ![]() en
en ![]()
On suppose que ![]() alors
alors ![]()
![]() Si l’on avait
Si l’on avait ![]() deux fonctions équivalentes au voisinage de
deux fonctions équivalentes au voisinage de ![]() ayant même signe au voisinage de
ayant même signe au voisinage de ![]() on aurait
on aurait ![]() pour
pour ![]() proche de
proche de ![]() et
et ![]() ce qui est absurde.
ce qui est absurde.
![]() On en déduit que
On en déduit que ![]() et donc
et donc ![]()
Puis comme ![]()
![]()
On aurait
![]()
![]() et
et ![]()
![]()
Les dérivées à droite et à gauche de ![]() en
en ![]() sont différentes, donc
sont différentes, donc ![]() n’est pas dérivable en
n’est pas dérivable en ![]() On aboutit à une contradiction. On a établi que
On aboutit à une contradiction. On a établi que ![]()
La réciproque de ce résultat est vraie et le tout s’appelle le théorème de Glaeser.
PROF DE MATHS PARTICULIER
Des cours de qualité et enseignants aguerris
Préparer des concours ou s'exercer
Avis Google France ★★★★★ 4,9 sur 5
2. Convexité
Méthode 3 : Comprendre quelque chose à la convexité.
![]() On rappelle qu’une fonction
On rappelle qu’une fonction ![]() définie sur un intervalle
définie sur un intervalle ![]() à valeurs dans
à valeurs dans ![]() est convexe sur
est convexe sur ![]() (respectivement concave sur
(respectivement concave sur ![]() ) si :
) si :
pour ![]() et pour tout
et pour tout ![]() on a
on a
![]()
(respectivement
![]()
![]() ).
).
Graphiquement, si l’on note ![]() le graphe de la fonction
le graphe de la fonction ![]() et
et ![]() le point d’abscisse
le point d’abscisse ![]() de
de ![]()
![]() est convexe (respectivement concave) sur
est convexe (respectivement concave) sur ![]() si, et seulement si pour tout
si, et seulement si pour tout ![]() dans
dans ![]() le graphe
le graphe ![]() est en dessous (respectivement au-dessus) du segment
est en dessous (respectivement au-dessus) du segment ![]() (cela s’appelle une corde).
(cela s’appelle une corde).
![]()
![]() est convexe si, et seulement si, pour tout
est convexe si, et seulement si, pour tout ![]()
![]()
![]() tel que
tel que 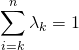 et pour tout
et pour tout ![]()
![Rendered by QuickLaTeX.com \[f \left( \displaystyle\sum_{k=1}^n \lambda_k x_k \right) \le \displaystyle\sum_{k=1}^n \lambda_k f \left( x_k \right).\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-8b85c4732b59c1bbdf1506439b7145b6_l3.png)
C’est l’inégalité de Jensen.
![]() Si
Si ![]() est dérivable sur un intervalle
est dérivable sur un intervalle ![]()
![]() est convexe sur
est convexe sur ![]()
![]()
![]() est croissante sur
est croissante sur ![]()
![]() pour tout
pour tout ![]() le graphe de
le graphe de ![]() est au dessus de sa tangente en
est au dessus de sa tangente en ![]()
Soit ![]() alors pour tout
alors pour tout ![]() on a
on a ![]()
![]() La définition n’est pas toujours simple à utiliser pour étudier la convexité d’une fonction. Soit
La définition n’est pas toujours simple à utiliser pour étudier la convexité d’une fonction. Soit ![]() un intervalle et
un intervalle et ![]() l’intervalle
l’intervalle ![]() privé de ses bornes éventuelles.
privé de ses bornes éventuelles.
On suppose que ![]() est continue sur
est continue sur ![]() et deux fois dérivable sur
et deux fois dérivable sur ![]() Il suffit d’appliquer le résultat suivant :
Il suffit d’appliquer le résultat suivant : ![]() est convexe (respectivement concave) sur
est convexe (respectivement concave) sur ![]() si, et seulement si
si, et seulement si ![]() (respectivement
(respectivement ![]() ) sur
) sur ![]()
La convexité sert généralement dans les questions suivantes :
![]() les inégalités qui peuvent se déduire de la convexité ou de l’inégalité de Jensen, on peut envisager cette méthode en présence de réels positifs dont la somme est égale à
les inégalités qui peuvent se déduire de la convexité ou de l’inégalité de Jensen, on peut envisager cette méthode en présence de réels positifs dont la somme est égale à ![]()
![]() d’inégalités conséquences de la position du graphe de
d’inégalités conséquences de la position du graphe de ![]() par rapport à ses tangentes,
par rapport à ses tangentes,
![]() dans le tracé d’un graphe d’une fonction que l’on vous a fait étudier au préalable : si
dans le tracé d’un graphe d’une fonction que l’on vous a fait étudier au préalable : si ![]() (respectivement
(respectivement ![]() ), alors localement (comprendre sur un voisinage de
), alors localement (comprendre sur un voisinage de ![]() ), le graphe de
), le graphe de ![]() est approximativement un morceau de parabole tournée vers le haut (respectivement vers le bas).
est approximativement un morceau de parabole tournée vers le haut (respectivement vers le bas).
Exemple : 1) Montrer que la fonction ![]() est convexe sur
est convexe sur ![]() En déduire que, pour tout
En déduire que, pour tout ![]()
![]()
2) En utilisant la convexité de ![]() montrer que pour tout
montrer que pour tout ![]()
![]()
Cette inégalité s’appelle l’inégalité arithmético-géométrique.
3) En déduire que si ![]()

![]()
Réponse :
1) On a ![]() Il s’ensuit que
Il s’ensuit que ![]() est convexe sur
est convexe sur ![]()
2) Si l’un des ![]() est nul, l’inégalité est évidente car le terme de gauche vaut alors
est nul, l’inégalité est évidente car le terme de gauche vaut alors ![]() Ainsi on suppose que pour tout
Ainsi on suppose que pour tout ![]()
![]() On applique l’inégalité de Jensen à la fonction
On applique l’inégalité de Jensen à la fonction ![]() avec
avec ![]() dont la somme vaut
dont la somme vaut ![]() pour avoir
pour avoir
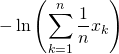
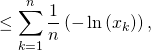
soit
![]()
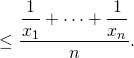
Méthode 2 : Montrer qu’un point est un point d’inflexion.
Soit ![]() est fonction définie sur un intervalle
est fonction définie sur un intervalle ![]() deux fois dérivable.
deux fois dérivable.
Soit ![]() on dit que le graphe de
on dit que le graphe de ![]() admet un point d’inflexion en
admet un point d’inflexion en ![]() si :
si :
![]()
![]()
![]()
![]() change de signe en
change de signe en ![]()
Géométriquement, le graphe de ![]() traverse sa tangente au point
traverse sa tangente au point ![]()
Exemple : Soit la fonction ![]() définie sur
définie sur ![]() définie par
définie par ![]()
Montrer que le graphe de ![]() a un unique point d’inflexion. Préciser ses coordonnées.
a un unique point d’inflexion. Préciser ses coordonnées.
Réponse : ![]() est bien deux fois dérivable sur
est bien deux fois dérivable sur ![]() . Pour tout
. Pour tout ![]() on a
on a
![]()
![]()
L’équation ![]() a pour unique solution
a pour unique solution ![]() De plus,
De plus, ![]() change de signe en
change de signe en ![]() En effet, pour
En effet, pour ![]() on a
on a ![]() et pour
et pour ![]() on a
on a ![]()
Finalement, le point ![]() est l’unique point d’inflexion pour la courbe de
est l’unique point d’inflexion pour la courbe de ![]()
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Vous trouverez ci-dessous d’autres chapitres de maths au programme d’ECG1 sous forme de cours en ligne, avec exercices et corrigés :


