Mon parcours pour réussir en maths
J'aprends le cours par coeur
Je travaille avec un prof de maths
Je travaille entre chaque séance
Avis Google France
★★★★★ 4,8 sur 5
Cours de maths sur les équations de droites en seconde générale
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Seconde générale
Notre cours sur les équations de droites offre aux élèves de seconde une compréhension approfondie de ces éléments clés des mathématiques. Vous apprendrez à travailler avec les équations cartésiennes, à comprendre la colinéarité et plus encore. Pour une parfaite maîtrise de ces concepts essentiels en mathématique, un prof de maths peut vous aider et vous éclairer sur zones qui restent encore floues.
Droites et vecteurs directeurs en seconde
Définition : Vecteur directeur d’une droite
On appelle vecteur directeur d’une droite ![]() tout vecteur
tout vecteur ![]() où
où ![]() et
et ![]() sont deux points distincts de
sont deux points distincts de ![]() .
.
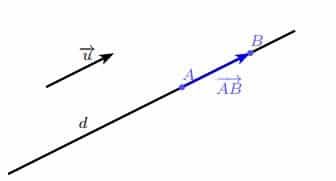
Propriété : Un vecteur ![]() est un vecteur directeur d’une droite
est un vecteur directeur d’une droite ![]() s’il existe deux points distincts
s’il existe deux points distincts ![]() et
et ![]() de
de ![]() tels que
tels que
![]() .
.
Remarque : Un vecteur directeur d’une droite ne peut pas être nul car les points ![]() et
et ![]() sont distincts.
sont distincts.
Propriété : Si ![]() est un vecteur directeur de la droite
est un vecteur directeur de la droite ![]() ,
,
Alors tout vecteur non nul colinéaire à ![]() est aussi vecteur directeur de
est aussi vecteur directeur de ![]() .
.
Exemple : Dans un repère du plan, on donne les points ![]() ,
, ![]() et le vecteur
et le vecteur ![]() .
.
Le vecteur ![]() est-il un vecteur directeur de la droite
est-il un vecteur directeur de la droite ![]() ?
?
Propriété : Soient ![]() une droite du plan, le point
une droite du plan, le point ![]() appartient à
appartient à ![]() et
et ![]() est un vecteur directeur de
est un vecteur directeur de ![]() .
.
Un point ![]() du plan appartient à
du plan appartient à ![]() si et seulement si les vecteurs
si et seulement si les vecteurs ![]() et
et ![]() sont colinéaires,
sont colinéaires,
C’est-à-dire ![]() .
.
Exemple : Soit ![]() la droite de vecteur directeur
la droite de vecteur directeur ![]() passant par le point
passant par le point ![]() .
.
Montrer que le point ![]() appartient à la droite
appartient à la droite ![]() .
.
Avis Google France ★★★★★ 4,9 sur 5UN PROF DE MATHS POUR EXCELLER
La pratique et la compréhension
clés de la réussiteCours de maths en ligne ou à domicile
Droites parallèles et droites sécantes
Propriété : Soient ![]() une droite de vecteur directeur
une droite de vecteur directeur ![]() et
et ![]() une droite de vecteur directeur
une droite de vecteur directeur ![]() .
.
Les droites ![]() et
et ![]() sont parallèles si et seulement si les vecteurs
sont parallèles si et seulement si les vecteurs ![]() et
et ![]() sont colinéaires,
sont colinéaires,
C’est-à-dire ![]() .
.
Les droites ![]() et
et ![]() sont sécantes si et seulement si les vecteurs
sont sécantes si et seulement si les vecteurs ![]() et
et ![]() ne sont pas colinéaires,
ne sont pas colinéaires,
C’est-à-dire ![]() .
.
Exemple : Soit ![]() la droite de vecteur directeur
la droite de vecteur directeur ![]() et les points
et les points ![]() ,
, ![]() .
.
Montrer que les droites ![]() et
et ![]() sont parallèles.
sont parallèles.
Équation cartésienne d’une droite
Définition : Équation cartésienne
Dans un repère du plan, toute droite ![]() admet une équation de la forme :
admet une équation de la forme : ![]() avec
avec ![]() .
.
Cette équation est appelée équation cartésienne de ![]() .
.
Remarque : Une droite admet une infinité d’équations cartésiennes.
Ainsi, la droite ![]() d’équation
d’équation ![]() a aussi pour équation
a aussi pour équation ![]() ou toute équation équivalente.
ou toute équation équivalente.
Propriété : ![]() ,
, ![]() et
et ![]() sont des nombres réels avec
sont des nombres réels avec ![]() .
.
Dire que ![]() admet pour équation
admet pour équation ![]() signifie qu’un point
signifie qu’un point ![]() appartient à la droite
appartient à la droite ![]() si, est seulement si, ses coordonnées vérifient cette équation (
si, est seulement si, ses coordonnées vérifient cette équation (![]() ).
).
Exemple : Soit ![]() la droite du plan d’équation
la droite du plan d’équation ![]() .
.
Le point ![]() appartient-il à
appartient-il à ![]() ? Même question pour le point
? Même question pour le point ![]() ?
?
Prorpiété : Dans un repère du plan, toute droite admettant une équation de la forme : ![]() avec
avec ![]() admet
admet ![]() comme vecteur directeur.
comme vecteur directeur.
Exemple : Dans un repère du plan, on donne le point ![]() et le vecteur
et le vecteur ![]() .
.
Déterminer une équation cartésienne de la droite ![]() passant par
passant par ![]() et de vecteur directeur
et de vecteur directeur ![]() .
.
Exemple : Dans un repère du plan, déterminer une équation cartésienne de la droite ![]() passant par les points
passant par les points ![]() et
et ![]() .
.
Équation réduite d’une droite
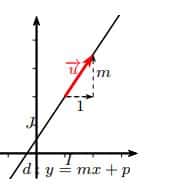
Définition : Équation réduite
Toute droite ![]() non parallèle à l’axe des ordonnées admet une unique équation de la forme
non parallèle à l’axe des ordonnées admet une unique équation de la forme ![]() où
où ![]() et
et ![]() sont des nombres réels.
sont des nombres réels.
Cette équation est l’équation réduite de la droite ![]() .
.
Remarque : Toute droite parallèle à l’axe des ordonnées à une unique équation de la forme ![]() (où
(où ![]() un nombre réel).
un nombre réel).
Elle n’a ni pente, ni ordonnée à l’origine.
Exemple : Soit ![]() la droite d’équation cartésienne
la droite d’équation cartésienne ![]() . Donner l’équation réduite de
. Donner l’équation réduite de ![]() .
.
Propriété : Dans un plan muni d’un repère, le vecteur ![]() est un vecteur directeur de la droite d’équation réduite
est un vecteur directeur de la droite d’équation réduite ![]() .
.
Exemple : Soit ![]() la droite d’équation réduite
la droite d’équation réduite ![]() .
.
Donner deux vecteurs directeurs de la droite ![]() .
.
Exemple : Soient ![]() la droite d’équation cartésienne
la droite d’équation cartésienne ![]() et
et ![]() la droite d’équation réduite
la droite d’équation réduite ![]() .
.
Montrer que ![]() et
et ![]() sont parallèles.
sont parallèles.
Systèmes linéaires de deux équations à deux inconnues
Définition : Equation à deux inconnues
Un système linéaire de deux équations à deux inconnues est la donnée de deux équations d’inconnues ![]() et
et ![]() de la forme :
de la forme :
![]()
Où ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() et
et ![]() sont des nombres réels donnés.
sont des nombres réels donnés.
Une solution de ce système est le couple de valeurs ![]() qui vérifie simultanément ces deux équations.
qui vérifie simultanément ces deux équations.
Résoudre ce système, c’est trouver tous ses couples de solutions.
Exemple : Le couple ![]() est-il solution du système
est-il solution du système
![]()
Interprétation graphique et nombre de couples de solutions
Soient les droites ![]() d’équation
d’équation ![]() et
et ![]() d’équation
d’équation ![]() .
.
Soit le système : ![]()
Résoudre le système ![]() , c’est déterminer les coordonnées des points d’intersection éventuels des droites
, c’est déterminer les coordonnées des points d’intersection éventuels des droites ![]() et
et ![]() .
.
Soient ![]() et
et ![]() les vecteurs directeurs respectifs de
les vecteurs directeurs respectifs de ![]() et
et ![]() .
.
On a donc ![]()
On distingue 3 possibilités pour l’ensemble des couples solutions ![]() du système
du système ![]() :
:
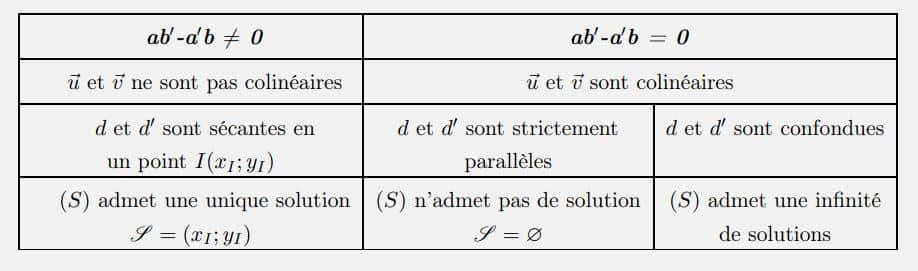
Exemple : Pour chaque système, discuter de l’existence des solutions.
![]()
![]()
![]()
Méthodes de résolution algébriques d’un système par substitution
Exemple :
On isole une inconnue dans une équation. Par exemple, ![]() dans la seconde équation :
dans la seconde équation :
![]()
![Rendered by QuickLaTeX.com \[\Leftrightarrow \left\{\begin{array}{l}3x-2y=2\\x= \fbox{$2y$}\end{array}\right.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-250e1cc77b9dfd7787a111b55599f40d_l3.png)
On remplace (ou substitue) ![]() par son expression en fonction de
par son expression en fonction de ![]() (ici,
(ici, ![]() ) dans la première équation, afin de faire disparaître la variable
) dans la première équation, afin de faire disparaître la variable ![]() :
:
![Rendered by QuickLaTeX.com \[(S)\Leftrightarrow \left\{\begin{array}{l}3\times\fbox{$2y$}-2y=2\\x=2y\end{array}\right. \]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-66aa13489549a833b8c9cd9adeac2b53_l3.png)
![]()
![]()
On résout l’équation avec une seule inconnue et on remplace le résultat dans l’autre :
![Rendered by QuickLaTeX.com \[(S)\Leftrightarrow \left\{\begin{array}{l}y=\dfrac 24=\frac 12\\x=2y\end{array}\right.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-b5c1346d01257201d1aad6539b4eece5_l3.png)
![Rendered by QuickLaTeX.com \[\Leftrightarrow \left\{\begin{array}{l}y=\dfrac 12\\x= 2\times \left(\frac 12\right)\end{array}\right.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-3384b4a440febb87885bd2fd5c3971e6_l3.png)
![Rendered by QuickLaTeX.com \[\Leftrightarrow \\ \left\{\begin{array}{l}y=\dfrac 12\\x=1\end{array}\right.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-2e2dc6d2c1e22879c276a880a821c554_l3.png)
Conclusion. Le système ![]() admet pour unique solution le couple
admet pour unique solution le couple ![]() où
où ![]() .
.
Méthodes de résolution algébriques d’un système par combinaison
Exemple :
On multiplie par exemple la première équation par le coefficient de ![]() dans la seconde et on multiplie la seconde équation par le coefficient de
dans la seconde et on multiplie la seconde équation par le coefficient de ![]() dans la première :
dans la première :
![]()
![]()
![]()
Les coefficients de ![]() sont identiques, on remplace une équation par la différence des deux :
sont identiques, on remplace une équation par la différence des deux :
![]()
![]()
On résout l’équation avec une seule inconnue et on remplace le résultat dans l’autre :
![]()
![Rendered by QuickLaTeX.com \[\Leftrightarrow \left\{\begin{array}{l}y=\dfrac 24=\dfrac 12\\3x-6\times \left(\dfrac 12\right)=0\end{array}\right. \]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-b4691ad00a93e5063de3ec712e4cbd74_l3.png)
![Rendered by QuickLaTeX.com \[\Leftrightarrow \\ \left\{\begin{array}{l}y=\dfrac 12\\3x-3=0\end{array}\right.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-c1b63d7004f3b2c0981a0b8d7a5561f0_l3.png)
![Rendered by QuickLaTeX.com \[\Leftrightarrow \\ \left\{\begin{array}{l}y=\dfrac 12\\x=\dfrac 33=1\end{array}\right.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-349aba359e012d25daacb3aee55b2289_l3.png)
Conclusion. Le système ![]() admet pour unique solution le couple
admet pour unique solution le couple ![]() où
où ![]() .
.
Avis Google France ★★★★★ 4,9 sur 5COURS DE MATHS A DOMICILE
Les meilleurs profs de maths pour
réussir sa scolarité En ligne ou à domicile
Retrouvez d’autres cours en ligne de maths seconde sur notre site :
- Fiche cours en maths pour comprendre les pourcentages en 2nde
- Cours de maths et exemples sur les statistiques en seconde
- Leçon de maths niveau seconde sur les probabilités
- Cours de mathématique en seconde : Ensembles et intervalles
- Maths : Fiche de révision sur l’arithmétique en 2nde
- Exercice de seconde sur les pourcentages
- Entrainement scorrigé ur les statistiques en seconde générale

