Cours en ligne Physique en Maths Sup

Chapitres Physique en MPSI, PCSI, MP2I, PTSI

Cours de Physique : Propagation en maths sup

Name: Groupe Réussite: Cours particuliers, stages intensifs de révision
Brand: Groupe Réussite
SKU: Cours Particuliers
Rating: 4.9 (1049 reviews)

Résumé de cours Exercices et corrigés

Cours en ligne de physique en Maths Sup

Ce cours gratuit de physique chimie en MPSI, PTSI, PCSI vous encouragera pour réviser le cours de la propagation. Si vous souhaitez améliorer vos résultats en prépa, n’hésitez pas à prendre un cours en physique chimie. Nous sommes là pour vous guider, quel que soit votre niveau scolaire, car nous croyons en l’idée d’un apprentissage accessible à tous. GR n’est pas qu’une plateforme de cours particuliers.

Résumé de cours et méthodes — maths sup propagation

Plan :

A. Signaux et spectres associés
B. Onde progressive

PRENDRE DES COURS DE PHYSIQUE CHIMIE

C’est comprendre et réussir

A. Signaux et spectres associés

1. Signal et composantes harmoniques

Un signal est une variation d’une grandeur physique au cours du temps.
On peut le modéliser par une fonction $s(t)$
On démontre que $s(t)$ peut s’écrire comme la somme de fonctions sinusoïdales du temps du type
$C(\omega)\cos(\omega y+\varphi(\omega))$
* $\omega$ est la pulsation, la fréquence associée est $f$ avec $\omega=2\pi f$
* $C(\omega)$ est l’amplitude de la composante de pulsation $\omega$
* $\varphi(\omega)$ est la phase de la composante de pulsation $\omega$
*Pour $\omega =0$ on parle de composante continue, et la phase est nulle.

Exemple.

Un accord joué par un orchestre de musiciens
est assimilable à un signal acoustique. Que représentent les notes
écrites sur la partition du chef d’orchestre ?

Correction :

Chaque note est caractérisée par sa fréquence (celle du LA du diapason vaut 440 Hz), et donc par sa pulsation $\omega=2\pi f$
La nuance (doux ou fort) permet de définir l’amplitude.

2. Spectre

Le spectre est une représentation graphique des composantes spectrales du signal $s(t)$
On distingue
* le spectre en amplitude donnant l’amplitude $C$ en fonction de la pulsation $\omega$ ou de la fréquence $f$ en abscisse. Un spectre discret, dans lequel les fréquences présentes dans le signal peuvent être numérotées, est représenté sou la forme de bâtons verticaux dont la hauteur est proportionnelle à l’amplitude
* le spectre en phase donnant la phase $\varphi$ en fonction de la pulsation $\omega$ ou de la fréquence $f$ en abscisse. Un spectre discret est représenté sou la forme de bâtons verticaux dont la hauteur est proportionnelle à la phase.
On peut transformer :
$\sin(\omega t)=\cos(\omega t-\pi/2)$
$-\cos(\omega t)=\cos(\omega t+\pi)$

Exemples.

1. Quel est le spectre du signal

$s(t)=2\cos(\omega_0 t)-\cos(2\omega_0 t)$

2. Quelle est l’expression mathématique du signal $u(t)$ dont voici les spectres en amplitude et en phase

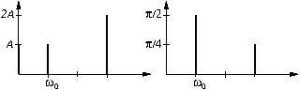
Correction :

1. On peut écrire
$s(t)=2\cos(\omega_0 t)+\cos(\2\omega_0 t+\pi)$
Le spectre en phase est formé d’un bâton de hauteur nulle pour $\omega=\omega_0$ et d’un bâton de hauteur $\pi$ pour $\omega=2\omega_0$
Le spectre en amplitude est formé d’un bâton de hauteur 2 pour $\omega=\omega_0$ et d’un bâton de hauteur 1 pour $\omega=2\omega_0$
2. On identifie les trois composantes, les pulsations, les amplitudes et les phases associées sur les graphiques
$u(t)=A+A\cos(\omega_0+\pi/2)$

$+2A\cos(2\omega_0t+\pi/4)$

COURS DE PHYSIQUE-CHIMIE

Nous avons sélectionné pour vous les meilleurs profs particuliers.

POUR ACCÉLÉRER MA PROGRESSION EN PHYSIQUE-CHIMIE, JE TROUVE DES

Avis Google France ★★★★★ 4,9 sur 5

B. Onde progressive

1. Principe ondulatoire

Une onde est définie par le principe suivant :

« Ce qui se passe ici et maintenant est ce qui s’est passé là-bas il y a quelques temps, ou bien ce qui se passer là-bas dans quelques temps. »

Pour une onde qui se propage sur un axe $x$ , ceci se traduit mathématiquement par

* onde se propageant dans le sens des $x$ croissants :

$f(x,t)=f(0,t-\frac{x}{c})$

* onde se propageant dans le sens des $x$ décroissants :

$f(x,t)=f(0,t+\frac{x}{c})$

$c$ est la célérité de l’onde et $f(x,t)$ est le signal.

On distingue deux types de représentations graphiques du signal.

* Si on fixe $x$ , on étudie ce qui se passe à cette abscisse au cours du temps : c’est l’histoire du point d’abscisse $x$ .

* Si on fixe $t$ , on étudie la forme du signal en fonction de $x$ : c’est la géographie du signal.

Exemple.

Une onde mécanique se propage le long d’une corde tendue. Voici les histoires de deux points : $A$ d’abscisse $x_A=0,50~\mathrm{m}$ et $B$ d’abscisse $x_B=0,75~\mathrm{m}$

Dans quel sens et à quelle célérité se propage l’onde ?

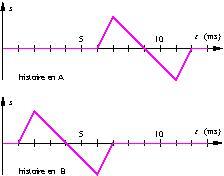
Correction :

L’onde se propage dans le sens des $x$ décroissants car la vibration commence en A à la date $t=6~\mathrm{ms}$ , donc plus tard qu’en B où elle commence à $t=1~\mathrm{ms}$

Le décalage temporel vaut $\tau=5~\mathrm{ms}$ pour une distance $\Delta x=x_B-x_A=0,25~\mathrm{m}$ .

On en déduit

$\displaystyle{c=\frac{\Delta x}{\tau}=100~\mathrm{m\cdot s^{-1}}}$

2. Ondes progressives sinusoïdales (ou harmoniques)

Lorsque le signal en un point est sinusoïdal et que l’onde se propage, alors on parle d’onde progressive sinusoïdale.

Sa forme générale est

$f(x,t)=A\cos(\omega t\pm kx+\varphi)$

* $A$ est l’amplitude, son unité est celle de $f$

* $\omega$ est la pulsation,en $\mathrm{rad\cdot s^{-1}}$ ,

* $f=\frac{\omega}{2\pi}$ est la fréquence en Hz,

* $T=\frac{2\pi}{\omega}$ est la période temporelle en s

* $k$ est la pulsation spatiale en $\mathrm{rad\cdot m^{-1}}$

* $\lambda=\frac{2\pi}{k}$ est la longueur d’onde (période spatiale) en m

* le signe – correspond à une propagation dans le sens des $x$ croissants, le signe + dans le sens des $x$ décroissants

* $\varphi$ est la phase de l’onde en rad.

Si on note $c$ la célérité de l’onde alors

$\omega = kc$ , $\lambda =cT$ , $\lambda=\frac{c}{f}$

Exemple.

Déterminer la fréquence, la longueur d’onde et la célérité de l’onde définie par

$\displaystyle{f(x,t)=5\cos\left(100\pi t-5\pi x+\frac{\pi}{3}\right)}$

Correction :

* $f=\frac{100\pi}{2\pi}=50~\mathrm{Hz}$

* $\displaystyle{\lambda=\frac{2\pi}{5\pi}=0,40~\mathrm{m}}$

* $c=\lambda\cdot f=20~\mathrm{m\cdot s^{-1}}$

COURS PARTICULIERS EN LIGNE

Nous avons sélectionné pour vous les meilleurs professeurs particuliers.

POUR ACCÉLÉRER MA PROGRESSION

Avis Google France ★★★★★ 4,9 sur 5

Les cours en ligne de physique en Maths Sup permettent aux élèves de revoir certaines notions de cours plus en profondeur. En effet, les cours en prépa se déroulent très vite, utilisez les cours en ligne permet de pouvoir combler des petites lacunes. Révisez par exemple :

Cours de Physique : Propagation en maths sup

Résumé de cours et méthodes — maths sup propagation

Plan :

PRENDRE DES COURS DE PHYSIQUE CHIMIE

C’est comprendre et réussir

A. Signaux et spectres associés

1. Signal et composantes harmoniques

2. Spectre

COURS DE PHYSIQUE-CHIMIE

Nous avons sélectionné pour vous les meilleurs profs particuliers.

POUR ACCÉLÉRER MA PROGRESSION EN PHYSIQUE-CHIMIE, JE TROUVE DES

B. Onde progressive

1. Principe ondulatoire

2. Ondes progressives sinusoïdales (ou harmoniques)

COURS PARTICULIERS EN LIGNE

Nous avons sélectionné pour vous les meilleurs professeurs particuliers.

POUR ACCÉLÉRER MA PROGRESSION

Contact

Qui sommes-nous ?

Nous rejoindre

Copyright @ GROUPE REUSSITE - Mentions légales