Chapitres Maths en ECS2
Cours : Réduction des endomorphismes en ECS2
Résumé de cours Exercices Corrigés
Cours en ligne de Maths en ECS2
Ce résumé de cours concernant les réductions des endomorphismes est primordial de le maîtriser parfaitement, car elles revêtent une importance cruciale. Si vous rencontrez des difficultés, n’hésitez pas à solliciter l’assistance de cours de maths en ligne.
Cours ECS 2 : Valeurs propres, Vecteurs propres et Réduction
1. Eléments propres : présentation
Dans ce chapitre, ![]() est un espace vectoriel de dimension
est un espace vectoriel de dimension ![]() ,
, ![]() , sur
, sur ![]() , (
, (![]() ou
ou ![]() ),
),
![]() est une base de
est une base de ![]() ,
, ![]() est un endomorphisme de
est un endomorphisme de ![]() ,
, ![]() est la matrice dans la base
est la matrice dans la base ![]() de
de ![]() .
.
Méthode 1 : Comment savoir si ![]() ,
, ![]() , est un vecteur propre de
, est un vecteur propre de ![]() ?
?
Si ![]() ,
, ![]() n’est pas un vecteur propre.
n’est pas un vecteur propre.
Si ![]() , on calcule
, on calcule ![]() . Si
. Si ![]() ,
, ![]() ,
, ![]() est vecteur propre de
est vecteur propre de ![]() associé à la valeur propre
associé à la valeur propre ![]() .
.
Exemple : ![]() ,
, ![]() est la base canonique de
est la base canonique de ![]() ,
, ![]() ,
, ![]() .
.
Les vecteurs suivants sont-ils vecteurs propres de ![]() :
:
Réponse :
- Non
- Oui, attaché à la valeur propre
 .
.
PROF DE MATHS PARTICULIER
Des cours de qualité et enseignants aguerris
Préparer des concours ou s'exercer
Avis Google France ★★★★★ 4,9 sur 5
Méthode 2 : Comment savoir si ![]() ,
, ![]() , est valeur propre de
, est valeur propre de ![]() (ou de
(ou de ![]() )? si
)? si ![]() est valeur propre de
est valeur propre de ![]() (ou de
(ou de ![]() )?
)?
![]() est valeur propre de
est valeur propre de ![]() si et seulement si
si et seulement si ![]() n’est pas injective (
n’est pas injective (![]() est valeur propre de
est valeur propre de ![]() si et seulement si
si et seulement si ![]() est non inversible).
est non inversible).
En particulier, ![]() est valeur propre de
est valeur propre de ![]() si et seulement si
si et seulement si ![]() n’est pas injective (ou
n’est pas injective (ou ![]() est valeur propre de
est valeur propre de ![]() si et seulement
si et seulement ![]() n’est pas inversible) .
n’est pas inversible) .
Exemple : Quelles sont les valeurs propres de :
 ?
?- L’application nulle ?
Réponse :
- 1 est la seule valeur propre
- 0 est la seule valeur propre
Méthode 3 : Si ![]() est valeur propre de
est valeur propre de ![]() , comment trouver le sous-espace propre associé?
, comment trouver le sous-espace propre associé?
Le sous-espace propre de ![]() associé à
associé à ![]() est
est ![]() , où :
, où :
![]() =
=![]()
=![]() =
=![]()
=![]() =
=![]() .
.
En particulier, le sous-espace propre associé à la valeur propre ![]() est
est ![]() .
.
Exemple :
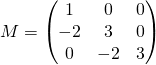 . Justifier que
. Justifier que ![]() est valeur propre de
est valeur propre de ![]() et trouver le sous-espace propre associé.
et trouver le sous-espace propre associé.
Méthode 4 : Si ![]() est valeur propre de
est valeur propre de ![]() , comment trouver les vecteurs propres de
, comment trouver les vecteurs propres de ![]() associés à
associés à ![]() ?
?
Ce sont les vecteurs non nuls qui vérifient ![]() .
.
Exemple :
![]() est un endomorphisme de
est un endomorphisme de ![]() qui admet la valeur propre
qui admet la valeur propre ![]() . Le sous-espace propre de
. Le sous-espace propre de ![]() associé à
associé à ![]() est
est ![]() .
.
Les vecteurs propres de ![]() sont les
sont les ![]() ,
, ![]() ?
?
Réponse : Non, ![]() est vecteur propre si et seulement si
est vecteur propre si et seulement si ![]() .
.
2. Recherches des valeurs et vecteurs propres
Méthode 5 : Comment utiliser les éléments propres de ![]() pour trouver ceux de :
pour trouver ceux de :
(i) ![]() ?
?
(ii) ![]() ,
, ![]() ?
?
(iii) ![]() , où
, où ![]() est un polynôme?
est un polynôme?
Si ![]() est valeur propre de
est valeur propre de ![]() et si
et si ![]() est un vecteur propre associé (
est un vecteur propre associé (![]() ,
, ![]() ), alors
), alors
(i) ![]()
(ii) ![]()
(iii) ![]() ,
,
donc ![]() ,
, ![]() ,
, ![]() sont valeurs propres de
sont valeurs propres de ![]() ,
,
![]() ,
, ![]() , et
, et ![]() est vecteur propre associé.
est vecteur propre associé.
Exemple : ![]() a pour valeurs propres
a pour valeurs propres ![]() et
et ![]() .
.
A-t-on ![]() ?
?
Méthode 6 : Comment trouver le spectre de ![]() (ou de
(ou de ![]() )?
)?
Le spectre de ![]() (ou de
(ou de ![]() ) est l’ensemble des valeurs propres de
) est l’ensemble des valeurs propres de ![]() (ou de
(ou de ![]() ).
).
(i) Si ![]() est triangulaire, les valeurs propres de
est triangulaire, les valeurs propres de ![]() (ou de
(ou de ![]() ) sont les coefficients diagonaux de
) sont les coefficients diagonaux de ![]() .
.
(ii) On sait que ![]() (ou
(ou ![]() ) admet un polynôme annulateur non nul.
) admet un polynôme annulateur non nul.
Si ![]() est un tel polynôme (
est un tel polynôme ( ![]() (ou
(ou ![]() ) ), les valeurs propres de
) ), les valeurs propres de ![]() (ou de
(ou de ![]() ) sont à chercher parmi les racines de
) sont à chercher parmi les racines de ![]() .
.
(iii) En général, on résout l’équation ![]() , d’inconnue
, d’inconnue ![]() , (ou le système fourni par l’équation matricielle
, (ou le système fourni par l’équation matricielle ![]() , d’inconnue
, d’inconnue ![]() ),
),
et on discute suivant les valeurs de ![]() : si pour
: si pour ![]() on obtient d’autres solutions que
on obtient d’autres solutions que ![]() , alors
, alors ![]() est valeur propre,
est valeur propre,
sinon elle ne l’est pas.
Exemple : Trouver le spectre de 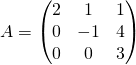 .
.
Réponse : ![]() .
.
Méthode 7 : Quand on a trouvé les valeurs propres de ![]() , que peut-on dire des sous-espaces propres?
, que peut-on dire des sous-espaces propres?
(i) Des sous-espaces propres associés à des valeurs propres distinctes sont en somme directe.
Donc, si ![]() sont des valeurs propres distinctes de
sont des valeurs propres distinctes de ![]() , on a:
, on a:
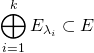 , et
, et
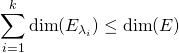 .
.
(ii) Si ![]() admet
admet ![]() valeurs propres distinctes, les sous-espaces propres de
valeurs propres distinctes, les sous-espaces propres de ![]() sont de dimension
sont de dimension ![]() et
et ![]() est somme directe de ces sous-espaces.
est somme directe de ces sous-espaces.
Exemple : ![]() ,
, ![]() , et
, et ![]() sont valeurs propres de
sont valeurs propres de ![]() , et on a:
, et on a: ![]() et
et ![]() .
.
Trouver le spectre de ![]() et la dimension des sous-espaces propres de
et la dimension des sous-espaces propres de ![]() .
.
Méthode 8 : Comment savoir qu’on a bien toutes les valeurs propres de ![]() (ou de
(ou de ![]() )?
)?
(i) Des vecteurs propres associés à des valeurs propres distinctes forment une famille libre.
Une famille libre a au plus ![]() éléments, donc
éléments, donc ![]() admet au plus
admet au plus ![]() valeurs propres distinctes.
valeurs propres distinctes.
(ii) Des sous-espaces propres associés à des valeurs propres distinctes sont en somme directe.
Si ![]() sont valeurs propres de
sont valeurs propres de ![]() et si
et si 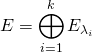 , ou si
, ou si
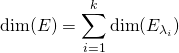 , (les deux conditions sont équivalentes), alors
, (les deux conditions sont équivalentes), alors
![]() .
.
Exemple : ![]() est un endomorphisme de
est un endomorphisme de ![]() ,
, ![]() n’est pas inversible,
n’est pas inversible, ![]() est valeur propre de
est valeur propre de ![]() et le sous-espace propre associé est de dimension
et le sous-espace propre associé est de dimension
![]() , et
, et ![]() ,
, ![]() .
.
Trouver le spectre de ![]() .
.
Réponse : ![]() est valeur propre de
est valeur propre de ![]() , donc
, donc ![]() ;
; ![]() est valeur propre de
est valeur propre de ![]() ,
, ![]() et
et ![]() appartiennent à
appartiennent à ![]() , et
, et
ces deux vecteurs forment une famille libre, donc ![]() . La somme des dimensions des sous-espaces propres associés à
. La somme des dimensions des sous-espaces propres associés à ![]() , et
, et
![]() est au moins
est au moins ![]() , donc égale à
, donc égale à ![]() . On a donc toutes les valeurs propres de
. On a donc toutes les valeurs propres de ![]() : ce sont
: ce sont ![]() , et
, et ![]() .
.
3. Réduction
Méthode 9 : Comment montrer que ![]() (ou
(ou ![]() ) est diagonalisable?
) est diagonalisable?
On doit montrer qu’il existe une base de ![]() dans laquelle la matrice de
dans laquelle la matrice de ![]() est diagonale (ou que
est diagonale (ou que ![]() est semblable à une matrice diagonale).
est semblable à une matrice diagonale).
Exemple : ![]() et
et ![]() ,
, ![]() .
. ![]() est-elle diagonalisable?
est-elle diagonalisable?
Réponse : Oui: ![]() est une base de
est une base de ![]() et la matrice de
et la matrice de ![]() dans cette base est
dans cette base est ![]() .
.
Méthode 10 : Comment caractériser une base de ![]() dans laquelle la matrice de
dans laquelle la matrice de ![]() est diagonale?
est diagonale?
La matrice de ![]() dans une base de
dans une base de ![]() est diagonale si et seulement si cette base est formée de vecteurs propres de
est diagonale si et seulement si cette base est formée de vecteurs propres de ![]() .
.
Exemple : ![]() . Peut-on trouver une base de
. Peut-on trouver une base de ![]() dans laquelle la matrice de
dans laquelle la matrice de ![]() soit diagonale?
soit diagonale?
Méthode 11 : Comment trouver une base de ![]() formée de vecteurs propres de
formée de vecteurs propres de ![]() ?
?
Si ![]() , et si
, et si 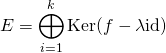
![]()
ou, ce qui est équivalent 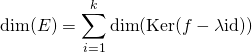
![]() , on obtient une base de
, on obtient une base de ![]()
en concaténant des bases ![]() de
de ![]() .
.
Si l’une ou l’autre des conditions équivalentes ![]() ou
ou ![]() n’est pas vérifiée, on ne peut pas trouver une telle base.
n’est pas vérifiée, on ne peut pas trouver une telle base.
Exemple : ![]() est un endomorphisme de
est un endomorphisme de ![]() ; le noyau de
; le noyau de ![]() est la droite vectorielle de base
est la droite vectorielle de base ![]() ;
; ![]() admet la valeur propre
admet la valeur propre ![]() et le
et le
sous-espace propre asocié a pour équation ![]() .
.
Peut-on trouver une base de ![]() formée de vecteurs propres de
formée de vecteurs propres de ![]() ?
?
Réponse : Oui: par exemple ![]() est une base de
est une base de ![]() ,
, ![]() appartient à
appartient à ![]() , donc
, donc
Méthode 12 : Dans quels cas simples peut-on dire que ![]() est diagonalisable si :
est diagonalisable si :
(i) ![]() admet
admet ![]() valeurs propres distinctes
valeurs propres distinctes ![]() ,
, ![]() est diagonalisable:
est diagonalisable: ![]() est semblable à
est semblable à
![]() , les sous-espaces propres sont de dimension
, les sous-espaces propres sont de dimension ![]() .
.
(ii) ![]() , c’est-à-dire si
, c’est-à-dire si ![]() est un projecteur,
est un projecteur, ![]() est diagonalisable:
est diagonalisable: ![]() , ou
, ou ![]() , ou sinon
, ou sinon ![]() ,
,
![]() ,
, ![]() , et
, et ![]() est semblable à
est semblable à ![]() , où
, où ![]() .
.
(iii) ![]() , c’est-à-dire si
, c’est-à-dire si ![]() est une symétrie vectorielle,
est une symétrie vectorielle, ![]() est diagonalisable:
est diagonalisable: ![]() , ou
, ou ![]() , ou sinon
, ou sinon
![]() , et
, et ![]() est semblable à
est semblable à ![]() , où
, où ![]() .
.
Exemple : ![]() vérifie
vérifie ![]() . Est-elle diagonalisable ?
. Est-elle diagonalisable ?
Méthode 13 : Quand on sait que ![]() est semblable à une matrice diagonale
est semblable à une matrice diagonale ![]() connue, comment retrouver à l’aide de
connue, comment retrouver à l’aide de ![]() les éléments propres de
les éléments propres de ![]() (ou de
(ou de ![]() )?
)?
(i) Le spectre de ![]() est l’ensemble des éléments diagonaux distincts de
est l’ensemble des éléments diagonaux distincts de ![]() .
.
(ii) Pour ![]() , la dimension de
, la dimension de ![]() est le nombre d’éléments diagonaux de
est le nombre d’éléments diagonaux de ![]() égaux à
égaux à ![]() .
.
(iii) Si ![]() , les colonnes de
, les colonnes de ![]() sont les matrices dans la base
sont les matrices dans la base ![]() de vecteurs propres
de vecteurs propres ![]() associés aux coefficients
associés aux coefficients
diagonaux ![]() de
de ![]() , et ces vecteurs forment une famille libre.
, et ces vecteurs forment une famille libre.
(iv) Si les éléments diagonaux de ![]() égaux à
égaux à ![]() sont
sont ![]() , alors
, alors
![]() .
.
(v) Si ![]() , et si, pour
, et si, pour ![]() ,
, ![]() ,
,
alors 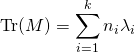 .
.
Exemple :
![]() , où
, où ![]() et
et 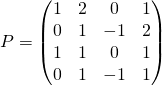 .
.
Trouver les valeurs propres de ![]() , donner la dimension et une base des sous-espaces propres.
, donner la dimension et une base des sous-espaces propres.
Réponse : ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Méthode 14 : Comment utiliser la réduction pour étudier ![]() ?
?
(i) Les sous-espaces propres de ![]() sont stables par
sont stables par ![]() , et la restriction de
, et la restriction de ![]() à
à ![]() est
est ![]() .
.
Si ![]() est somme directe de sous-espaces propres, et que l’on veut établir une propriété de
est somme directe de sous-espaces propres, et que l’on veut établir une propriété de ![]() , il suffit souvent de l’établir sur chaque sous-espace propre.
, il suffit souvent de l’établir sur chaque sous-espace propre.
(ii) Les calculs matriciels sont plus simples avec une matrice diagonale.
En particulier, si ![]() , alors, pour
, alors, pour ![]() ,
, ![]() .
.
Exemple : ![]() est un endomorphisme de
est un endomorphisme de ![]() , de matrice
, de matrice ![]() . Calculer
. Calculer ![]() .
.
Réponse : ![]() , si
, si ![]() et
et ![]() ,
, ![]() , donc
, donc
![]() .
.
Pour être sûr d’obtenir une bonne note en maths lors des concours post-prépa, entrainez-vous sur les divers cours en ligne de maths en ECS2 :

