Chapitres Maths en ECS2
Cours : Espaces vectoriels, matrices en ECS2
Résumé de cours Exercices Corrigés
Cours en ligne de Maths en ECS2
Ce cours en ligne sur les espaces vectoriels est une ressource qui vous accompagnera tout au long de votre parcours en ECS2. Il est important de bien assimiler les notions de manière complète. N’hésitez pas à solliciter l’aide d’un professeur particulier en maths si vous éprouvez le moindre besoin.
Matrices inversibles, Matrices de passage, Matrices semblables
1. Matrice d’un endomorphisme
Méthode 1 : Comment écrire la matrice dans la base ![]() de
de ![]() ?
?
La matrice dans ![]() de
de ![]() a
a ![]() lignes et
lignes et ![]() colonnes. Pour
colonnes. Pour ![]() , la
, la ![]() colonne de cette matrice est la matrice (colonne) de
colonne de cette matrice est la matrice (colonne) de ![]() dans
dans ![]() .
.
Exemple : Si ![]() ,
, ![]() , écrire
, écrire ![]() .
.
Réponse : ![]()
Méthode 2 : Comment savoir si une matrice ![]() à
à ![]() lignes et
lignes et ![]() colonnes est la matrice d’un endomorphisme de
colonnes est la matrice d’un endomorphisme de ![]() ? lequel?
? lequel?
![]() est la matrice de l’endomorphisme
est la matrice de l’endomorphisme ![]() défini par:
défini par: ![]() est linéaire et pour
est linéaire et pour ![]() la matrice de
la matrice de ![]() dans
dans ![]() est la
est la ![]() colonne de
colonne de ![]()
Méthode 3 : Comment calculer ![]() à l’aide des matrices ?
à l’aide des matrices ?
Si ![]() est la matrice (colonne) dans
est la matrice (colonne) dans ![]() de
de ![]() , la matrice dans
, la matrice dans ![]() de
de ![]() est
est ![]() .
.
Si ![]() est la
est la ![]() ligne de
ligne de ![]() , et si
, et si 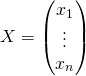 , la
, la ![]() coordonnée de
coordonnée de ![]() est
est ![]() , et
, et 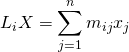
Méthode 4 : Si ![]() et
et ![]() sont deux endomorphismes de
sont deux endomorphismes de ![]() , comment calculer la matrice de
, comment calculer la matrice de ![]() ?
?
On effectue le produit des matrices de ![]() et
et ![]() dans la base
dans la base ![]() (en respectant l’ordre): si
(en respectant l’ordre): si ![]() ,
, ![]() et
et
![]() , alors
, alors
![]() . Pour
. Pour ![]() ,
, 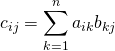 .
.
PROF DE MATHS PARTICULIER
Des cours de qualité et enseignants aguerris
Préparer des concours ou s'exercer
Avis Google France ★★★★★ 4,9 sur 5
2. Isomorphismes et matrices inversibles
Méthode 5 : Comment voir sur ![]() si
si ![]() est un isomorphisme (c’est-à-dire si
est un isomorphisme (c’est-à-dire si ![]() est bijective) ou non?
est bijective) ou non?
![]() est bijective si et seulement si
est bijective si et seulement si ![]() est inversible.
est inversible.
Si ![]() appartient à
appartient à ![]() ,
, ![]() ,
, ![]() est inversible si et seulement
est inversible si et seulement ![]() (
(![]() est le déterminant de
est le déterminant de ![]() ).
).
Si ![]() est triangulaire,
est triangulaire, ![]() est bijective si et seulement si les coefficients diagonaux de
est bijective si et seulement si les coefficients diagonaux de ![]() sont tous non nuls.
sont tous non nuls.
En général:
– si les colonnes de ![]() forment une famille libre, alors la famille
forment une famille libre, alors la famille ![]() est libre, donc c’est une base de
est libre, donc c’est une base de ![]() , donc
, donc ![]() est bijective; si les
est bijective; si les
colonnes de ![]() sont liées,
sont liées, ![]() n’est pas bijective.
n’est pas bijective.
– si l’équation ![]() (qui équivaut à
(qui équivaut à ![]() ), d’inconnue
), d’inconnue 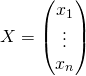 , a pour unique solution
, a pour unique solution ![]() , alors
, alors ![]() ,
,
donc ![]() est injective, et comme
est injective, et comme ![]() est de dimension finie,
est de dimension finie, ![]() est bijective; si cette équation admet d’autres solutions,
est bijective; si cette équation admet d’autres solutions, ![]() n’est pas injective, donc pas bijective.
n’est pas injective, donc pas bijective.
Exemple : 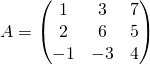 et
et 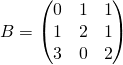 .
.
Dire si ![]() est un isomorphisme quand sa matrice dans la base
est un isomorphisme quand sa matrice dans la base ![]() est
est ![]() ?
?
Réponse : Les deux premières colonnes de ![]() sont proportionnelles, donc
sont proportionnelles, donc ![]() n’est pas inversible, donc si la matrice de
n’est pas inversible, donc si la matrice de ![]() est
est ![]() ,
, ![]() n’est pas un isomorphisme
n’est pas un isomorphisme
Méthode 6 : Comment savoir si ![]() est bijective et si elle l’est trouver la matrice de
est bijective et si elle l’est trouver la matrice de ![]() ?
?
Si ![]() où
où ![]() , alors
, alors ![]() .
.
En général, pour trouver ![]() ,on résout l’équation
,on résout l’équation ![]() où
où 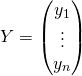 est donnée et
est donnée et
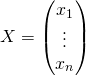 est l’inconnue (cette équation est équivalente à
est l’inconnue (cette équation est équivalente à ![]() , où
, où ![]() et
et ![]() ont pour matrices
ont pour matrices ![]() et
et ![]() dans
dans ![]() ). C’est une équation matricielle, qui se présente comme un système où les inconnues sont
). C’est une équation matricielle, qui se présente comme un système où les inconnues sont ![]() ,
, ![]() , et on peut résoudre ce système par la méthode que l’on veut (la méthode de Gauss en est un exemple).
, et on peut résoudre ce système par la méthode que l’on veut (la méthode de Gauss en est un exemple).
Méthode 7 : Comment montrer que ![]() est bijective et trouver
est bijective et trouver ![]() en utilisant un polynôme annulateur?
en utilisant un polynôme annulateur?
Exemple : ![]() .
. ![]() est-elle inversible? Si oui, exprimer
est-elle inversible? Si oui, exprimer ![]() à l’aide de
à l’aide de ![]() .
. ![]() est-elle inversible?
est-elle inversible?
Réponse : ![]() , donc
, donc ![]() est inversible et
est inversible et ![]() .
.
3. Matrices de passage
Méthode 8 : Comment écrire la matrice de passage ![]() de la base
de la base ![]() à une autre base
à une autre base ![]() de
de ![]() ? et la matrice de passage de
? et la matrice de passage de ![]() à
à ![]() ?
?
Si ![]() , pour
, pour ![]() , la
, la ![]() colonne de
colonne de ![]() est la matrice dans
est la matrice dans ![]() du vecteur
du vecteur
![]() .
.
La matrice ![]() est inversible et son inverse est
est inversible et son inverse est ![]() .
.
Exemple : Ecrire la matrice de passage de ![]() à
à ![]() quand
quand ![]() et
et ![]() . La matrice de passage est ?
. La matrice de passage est ?
Réponse : ![]()
Méthode 9 : Comment calculer la matrice d’un vecteur ou d’un endomorphisme dans une nouvelle base ![]() ?
?
Si ![]() appartient à
appartient à ![]() ,
, ![]() , et si
, et si ![]() appartient à
appartient à ![]() ,
, ![]() . En notant
. En notant ![]() la matrice de passage de
la matrice de passage de ![]() à
à ![]() , on obtient
, on obtient ![]() .
.
Méthode 10 : Comment savoir si une matrice est une matrice de passage?
Une matrice ![]() est une matrice de passage si et seulement si elle est carrée et inversible. Si c’est le cas, les colonnes
est une matrice de passage si et seulement si elle est carrée et inversible. Si c’est le cas, les colonnes ![]() de
de ![]() sont les matrices dans
sont les matrices dans ![]() de vecteurs
de vecteurs ![]() de
de ![]() .
.
La famille ![]() est une base de
est une base de ![]() et
et ![]() .
.
Exemple : La matrice ![]() est-elle une matrice de passage? Entre quelles bases?
est-elle une matrice de passage? Entre quelles bases?
Réponse : ![]() , donc
, donc ![]() est inversible, donc
est inversible, donc ![]() est la matrice de passage d’une base
est la matrice de passage d’une base ![]() à la base
à la base ![]() .
.
4. Matrices semblables et trace :
Méthode 11 : Quand peut-on dire que les matrices ![]() et
et ![]() sont semblables?
sont semblables?
![]() est semblable à
est semblable à ![]() (ou
(ou ![]() et
et ![]() sont semblables) si
sont semblables) si ![]() est la matrice de
est la matrice de ![]() dans une base
dans une base ![]() de
de ![]() , c’est-à-dire s’il existe une matrice
, c’est-à-dire s’il existe une matrice ![]() de
de ![]() telle que
telle que
![]() . Alors
. Alors ![]() .
.
Exemple : Montrer que ![]() et
et ![]() sont semblables.
sont semblables.
Réponse : ![]() est la matrice de
est la matrice de ![]() dans la base
dans la base ![]() , donc
, donc ![]() , donc
, donc ![]() et
et ![]() .
.
La matrice de ![]() dans la base
dans la base ![]() est
est ![]() , donc
, donc ![]() et
et ![]() sont semblables.
sont semblables.
Méthode 12 : Comment calculer des traces?
La trace d’une matrice carrée est la somme de ses coefficients diagonaux.
Une matrice carrée et sa transposée ont même trace.
Si ![]() appartiennent à
appartiennent à ![]() et si
et si ![]() appartient à
appartient à ![]() ,
, ![]() , et
, et ![]() .
.
Deux matrices semblables ont même trace.
Exemple : (i) 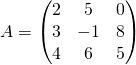 .
.
Calculer la trace de ![]() .
.
(ii) ![]() et
et ![]() sont deux matrices à
sont deux matrices à ![]() lignes et
lignes et ![]() colonnes inversibles.
colonnes inversibles.
Calculer la trace de ![]() .
.
Réponse :
(i) ![]() =
= ![]() =
= ![]() et
et
![]()
= ![]()
= ![]()
= ![]() .
.
(ii) ![]() donc
donc
Méthode 13 : Comment savoir si ![]() et
et ![]() sont semblables?
sont semblables?
Si ![]() et
et ![]() sont semblables, elles ont même rang (celui de
sont semblables, elles ont même rang (celui de ![]() ), elles sont toutes les deux inversibles (si
), elles sont toutes les deux inversibles (si ![]() est bijective) ou toutes les deux non inversibles (si
est bijective) ou toutes les deux non inversibles (si
![]() n’est pas bijective),
n’est pas bijective),
elles ont même trace.\par Si l’une de ces propriétés n’est pas vérifiée, ![]() et
et ![]() ne sont pas semblables. \par Si elles sont toutes vérifiées, on peut revenir à la définition et chercher une base
ne sont pas semblables. \par Si elles sont toutes vérifiées, on peut revenir à la définition et chercher une base ![]() telle que
telle que ![]() soit la matrice de
soit la matrice de ![]() dans
dans ![]() , ou chercher une matrice carrée P inversible telle que
, ou chercher une matrice carrée P inversible telle que ![]() .
.
Méthode 14 : Comment exploiter le fait que ![]() et
et ![]() sont semblables?
sont semblables?
Certains calculs se font plus simplement en utilisant ![]() .
.
Par exemple si ![]() et
et ![]() sont semblables, pour tout entier naturel
sont semblables, pour tout entier naturel ![]() ,
, ![]() et
et ![]() sont semblables (ce sont deux matrices de
sont semblables (ce sont deux matrices de ![]() ): si
): si ![]() ,
, ![]() .
.
Exemple : On sait que 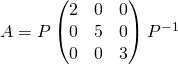 . Calculer
. Calculer ![]() .
.
Réponse : 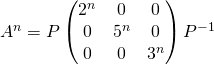 .
.
5. Sous-espaces stables :
Méthode 15 : Si ![]() est un sous-espace vectoriel de
est un sous-espace vectoriel de ![]() , comment savoir s’il est stable par
, comment savoir s’il est stable par ![]() ?
?
On prend un vecteur ![]() quelconque de
quelconque de ![]() . Si
. Si ![]() appartient toujours à
appartient toujours à ![]() , alors
, alors ![]() est stable par
est stable par ![]() .
.
Si on connait une famille génératrice ![]() de
de ![]() , il suffit de montrer que
, il suffit de montrer que ![]() appartiennent à
appartiennent à ![]() .
.
Exemple : ![]() est un projecteur,
est un projecteur, ![]() appartient à
appartient à ![]() et
et ![]() appartient à
appartient à ![]() .
. ![]() est-il stable par
est-il stable par ![]() ?
?
Réponse : Oui: ![]() et
et ![]() , donc
, donc ![]() et
et ![]() appartiennent à
appartiennent à ![]() .
.
Méthode 16 : Comment voir sur ![]() un sous-espace stable par
un sous-espace stable par ![]() ?
?
Si par exemple Si par exemple ![]() où
où ![]() est stable par
est stable par ![]() ,
, ![]() se décompose en blocs:
se décompose en blocs: ![]() où
où
![]() appartient à
appartient à ![]() . Inversement, si
. Inversement, si ![]() est de cette forme,
est de cette forme, ![]() est stable par
est stable par ![]() .
.
D’autres cours au programme de maths en ECS2 peuvent aussi être consultés gratuitement sur notre site :

