Résumé de cours Exercices et corrigés

Cours en ligne du Tage Mage

Ce cours est utile pour tout élève qui prépare le Tage Mage et souhaite réussir le sous test de conditions minimales.

Les conditions minimales

Le sous-test de conditions minimales traite des mêmes thèmes que le sous test 2 Calcul. Aussi les questions types sont dans l’ensemble identiques au sous test 2. C’est l’approche de ces questions qui est tout autre. En effet, il ne s’agit pas de résoudre un problème mais de savoir si l’on peut ou pourrait le résoudre. Il faut se demander « puis-je répondre à la question avec les informations dont je dispose ? » Il est évidemment nécessaire de bien maîtriser les fractions, les racines carrés et tous les chapitres de calcul.

L’élément clef est qu’il ne faut pas trouver la réponse mais simplement savoir si on peut la trouver et répondre en conséquence.

Répondre à la question  : c’est pouvoir trancher !

Comprendre en vidéo :

 

La méthodologie des conditions minimales

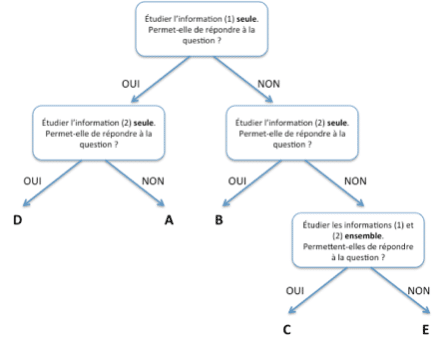
Il est indispensable de maîtriser la signification des 5 lettres qui correspondent aux 5 propositions. On répond :

• A si l’information (1) permet à elle seule de répondre à la question, et si l’information (2) à elle seule ne permet pas de répondre à la question.
• B si l’information (2) permet à elle seule de répondre à la question, et si l’information (1) à elle seule ne permet pas de répondre à la question
• C si les deux informations (1) et (2) ensemble permettent de répondre à la question, et aucune séparément ne le peut.
• D si chaque information permet séparément de répondre à la question.
• E si les deux informations ensemble ne permettent pas de répondre à la question.

Voici un moyen mnémotechnique pour différencier les réponses C et D :

• C comme Conjointement, si on peut répondre avec (1) et (2) ensemble.
• D comme Dis jointement, si on peut répondre avec (1) et (2) séparément.

On vous recommande d’appliquer la trame suivante à chaque question pour pouvoir répondre méthodiquement. En effet le risque est de « passer à côté » d’une possibilité de réponse. Aussi soyez rigoureux dans la démarche de résolution des questions de conditions minimales.

Trame à suivre :

Exemple de question dont la réponse est A

Question 1.

L’héritage d’un montant de 90 000 € de M. Duvigier est divisé entre son épouse et ses deux enfants. Combien a reçu le plus jeune de ses enfants ?

(1) Le plus jeune des enfants a reçu 20 000 € de moins que son frère aîné et 40 000 € de moins que l’épouse.

(2) L’épouse de M. Duvigier a reçu 55% du montant total de l’héritage.

Question 1 : Réponse A

Compréhension de l’énoncé :

Il fallait juste avoir en tête que : l’épouse + l’ainé + le plus jeune = 90 000 €

Information (1) seule permet de répondre.

Dans ce type de question, surtout en conditions minimales, être à l’aise avec le calcul littéral et la mise en équation est fondamental. On connaît ici le lien entre chaque personne, on va pouvoir poser une équation. Soit x le montant du plus jeune. Son frère a donc eu 20 000 € de plus que lui soit x + 20 000 et l’épouse 40 000 € de plus que lui soit x + 40 000.

Il suffit alors de résoudre : x + (x + 20 000) + (x + 40 000) = 90 000.

Inutile de résoudre cette équation, on sait qu’elle admet une solution (unique) et donc on pourra déterminer le montant de l’héritage du plus jeune enfant.

Information (2) seule ne permet pas de répondre.

On apprend uniquement que l’épouse a reçu 55% des 90 000 €. Certes on pourrait déterminer le montant de l’épouse (calcul inutile) mais ensuite on ne connaît pas la répartition entre les deux enfants. Équitable ou l’un en a-t-il reçu plus que l’autre ?

L’information (1) permis de répondre mais l’information (2) non. Réponse A.

Exemple de question dont la réponse est B

Question 2.

Combien Darius a-t-il acheté de cookies ?

(1) Darius a 8 euros.

(2) Si Darius avait eu deux fois plus d’argent, il aurait pu acheter quatre cookies supplémentaires.

Question 2 : Réponse B

Information (1) seule ne permet pas de répondre.

On ne sait pas combien coûte un cookie, impossible de savoir.

Information (2) seule est suffisante.

En doublant sa somme d’argent, il en achète 4 de plus. Cela signifie qu’avec sa somme initiale il en a acheté 4 également.

Un exemple pour mieux comprendre : supposons que Darius ait 10 euros au départ. S’il double sa somme, il aura 20 euros. Avec la somme supplémentaire (10 €) il achète 4 cookies. Donc avec sa somme initiale (10 €) il achète aussi 4 cookies.

L’information (1) n’a pas permis de répondre mais l’information (2) a permis. Réponse B.

Exemple de question dont la réponse est C

Question 3.

A est un nombre entier naturel inférieur à 100. Quelle est sa valeur ?

(1) A est un multiple de 11.

(2) A est un multiple de 6.

Question 3 : Réponse C

Vocabulaire : 

Deux nombres sont premiers entre eux s’ils n’ont aucun diviseur commun (excepté 1)

• 7 et 12 sont premiers entre, aucun diviseur commun
• 12 et 15 ne sont pas premiers entre eux car 3 est un diviseur commun

Information (1) seule n’est pas suffisante.

A est un multiple de 11, cela peut être : 11 ; 22 ; 33 ; 44 ; 55 etc.

Trop de possibilités, on ne peut pas connaître la valeur de A.

Information (2) seule n’est pas suffisante.

Même argument, les possibilités sont notamment : 6 ; 12 ; 18 ; 24 ; 30 etc.

Informations (1) et (2) ensemble permettent de répondre.

6 et 11 sont premiers entre eux, aussi si A est à la fois un multiple de 6 et de 11, c’est qu’il est multiple de 66. Et le seul multiple de 66 inférieur à 100 c’est 66. Le suivant est 2×66 = 132 trop grand.

Remarque : 

Si les deux nombres n’avaient pas été premiers entre eux comme 12 et 15, le premier nombre multiple de 12 et de 15 n’est pas 12×15 mais 60 (12×5 et 12×4)

L’information (1) seule n’a pas permis de répondre mais l’information (2) seule non plus. Mais en les combinant on a pu répondre. Réponse C.

 

Exemple de question dont la réponse est D

Question 4.

Combien vaut, en cm², l’aire de ce carré ?

(1) la longueur de sa diagonale est de 2,7 dm.

(2) Son périmètre vaut 0,76 m.

Question 4 : Réponse D

Rappel de cours : 

Si un carré est de coté a, alors :

• son aire vaut a²
• son périmètre vaut 4a
• sa diagonale vaut

Compréhension de la question :

On cherche l’aire du carré, aussi a-t-on besoin de la longueur du côté. Si on a le côté, on a l’aire du carré. Or d’après le rappel de cours précédent, l’aire, le périmètre, la diagonale dépendent, tous les trois, uniquement au côté. Autrement dit si on connaît l’une de ces données, on les connaît toutes.

Attention : 

Il ne fallait pas se laisser « impressionner » par les unités (cm, dm etc.) uniquement là pour essayer de vous déstabiliser. En effet, on ne cherche pas la valeur de l’aire du carré mais seulement si on est en mesure de la trouver avec les informations.

Information (1) seule suffit. On a la diagonale du carré, on peut retrouver le côté et donc l’aire.

En effet, d’après le cours si le côté est a, la diagonale vaut , il suffit alors de résoudre

pour déterminer a, on convertit en cm puis on calcule l’aire.

Information (2) seule suffit. À partir du périmètre, on peut retrouver le côté, il suffit de diviser par 4. Et une fois qu’on a le côté, on peut déterminer l’aire.

Conclusion :

Chaque information, seule, a permis de répondre à la question. Réponse D.

Exemple de question dont la réponse est E.

Question 5.

Une urne contient des boules rouges, blanches et noires. Quelle est la probabilité de tirer une boule noire ?

(1) Il y a autant de boule blanches que de boule noires.

(2) Il y a 10 boules noires.

Question 5 : Réponse E

Compréhension de la question :

Pour déterminer une probabilité dans ce cadre, il faudrait connaître le nombre de chaque boules ou bien leur proportion respective voire un pourcentage.

Information (1) seule est insuffisante. On n’a aucune information sur les boules rouges. Impossible de déterminer une probabilité.

Information (2) seule est insuffisante. Aucune information sur les blanches ni les rouges.

Informations (1) et (2) ensemble ne sont toujours pas suffisantes. On sait à présent qu’il y a 10 boules noires et 10 boules blanches mais toujours rien sur les rouges.

Impossible de répondre à la question, même en combinant (1) et (2), on répond E.

Pour réviser efficacement ce sous-test sur les conditions minimales, vous pouvez aussi vous entraîner sur les cours en ligne du sous-test 2 sur le calcul, comme :

• les fractions
• les pourcentages
• la vitesse
• les puissances
• la proportionnalité