Chapitres Maths en ECS2
Les corrigés classiques d’algèbre bilinéaire en ECS2
Résumé de cours Exercices Corrigés
Cours en ligne de Maths en ECS2
Corrigés classiques d’algèbre bilinéaire ECS2
Exercice 1 : Calcul de 
Si ![]() et
et ![]() sont deux éléments de
sont deux éléments de ![]() , on pose:
, on pose:
![]() =
= ![]()
Question 1 :
D’après l’énoncé, ![]() est de la forme
est de la forme ![]() , donc
, donc ![]() est une forme bilinéaire sur
est une forme bilinéaire sur ![]() :
: ![]() où
où ![]() , c’est-à-dire ici
, c’est-à-dire ici
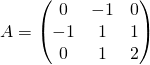 .
.
Question 2 :
La matrice ![]() est symétrique, donc
est symétrique, donc ![]() est symétrique.
est symétrique.
Question 3 :
On voit que ![]() , et
, et ![]() n’est pas le vecteur nul. Donc
n’est pas le vecteur nul. Donc ![]() n’est pas un produit scalaire.
n’est pas un produit scalaire.
Question 4 :
La matrice de ![]() (dans la base canonique) est
(dans la base canonique) est ![]() , donc
, donc ![]() , donc
, donc ![]() est bilinéaire et sa matrice est
est bilinéaire et sa matrice est ![]() :
: 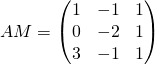 .
.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Exercice 2 : Produit scalaire
![]() ,
, ![]() , est muni de la base canonique
, est muni de la base canonique ![]() , et
, et ![]() est une application continue.
est une application continue.
On définit l’application ![]() par:
par:
![]() est bilinéaire, et, pour tous
est bilinéaire, et, pour tous ![]() de
de ![]() ,
, ![]() .
.
Question 1 :
En écrivant 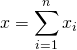 ,
, 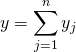 , et en utilisant la bilinéarité de
, et en utilisant la bilinéarité de ![]() , on obtient :
, on obtient :
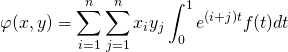 .
.
Question 2 :
On voit que ![]() , quelque soient
, quelque soient ![]() et
et ![]() , donc
, donc ![]() est symétrique.
est symétrique.
Pour tout ![]() de
de ![]() ,
,
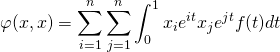
=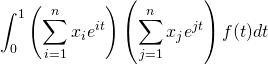
=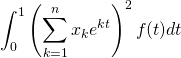 .
.
Comme ![]() est positive, la fonction intégrée est positive, et les bornes de l’intégrale sont dans l’ordre croissant, donc
est positive, la fonction intégrée est positive, et les bornes de l’intégrale sont dans l’ordre croissant, donc ![]() .
.
Si ![]() , comme la fonction intégrée est continue et positive, elle est nulle sur
, comme la fonction intégrée est continue et positive, elle est nulle sur ![]() , et comme
, et comme ![]() est strictement positive sur
est strictement positive sur ![]() , pour tout de
, pour tout de ![]() ,
, 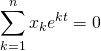 .
.
Le polynôme 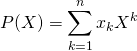 admet donc une infinité de racines (tous les
admet donc une infinité de racines (tous les ![]() ,
, ![]() ), donc c’est le polynôme nul, donc tous ses coefficients sont nuls. Donc pour tout
), donc c’est le polynôme nul, donc tous ses coefficients sont nuls. Donc pour tout ![]() de
de ![]() ,
, ![]() , donc
, donc ![]() .
.
Donc ![]() est définie positive.
est définie positive.
![]() est une forme bilinéaire, symétrique, définie positive, donc c’est un produit scalaire.
est une forme bilinéaire, symétrique, définie positive, donc c’est un produit scalaire.
Exercice 3 : Calcul de produit scalaire
![]() est l’ensemble des applications
est l’ensemble des applications ![]() continues sur
continues sur ![]() , telles que l’intégrale
, telles que l’intégrale
![]() converge.
converge.
Question 1 :
![]() est inclus dans l’espace vectoriel
est inclus dans l’espace vectoriel ![]() des applications définies sur
des applications définies sur ![]() , à valeurs dans
, à valeurs dans ![]() .
.
Question 2 :
La fonction nulle appartient à ![]() .
.
Si ![]() appartient à
appartient à ![]() et si
et si ![]() est un réel,
est un réel, ![]() appartient à
appartient à ![]() .
.
Si ![]() et
et ![]() appartiennent à
appartiennent à ![]() , pour tout
, pour tout ![]() de
de ![]() ,
, ![]() , donc
, donc
![]() , donc
, donc
![]()
![]() .
.
Par comparaison des fonctions intégrées, ![]() converge, donc
converge, donc ![]() appartient à
appartient à ![]() .
.
Donc ![]() est un sous-espace vectoriel de
est un sous-espace vectoriel de ![]() , donc
, donc ![]() est un espace vectoriel sur
est un espace vectoriel sur ![]() .
.
Question 3 :
Si ![]() et
et ![]() appartiennent à
appartiennent à ![]() , le intégrales
, le intégrales ![]() et
et
![]() convergent.
convergent.
Comme ![]() , par comparaison des fonctions intégrées,
, par comparaison des fonctions intégrées, ![]() converge.
converge.
Donc ![]() est bien une application de
est bien une application de ![]() dans
dans ![]() .
.
Pour tous ![]() et
et ![]() de
de ![]() ,
, ![]() , donc
, donc ![]() est symétrique.
est symétrique.
Si ![]() ,
, ![]() ,
, ![]() sont éléments de
sont éléments de ![]() , si
, si ![]() et
et ![]() sont des réels, par linéarité de l’intégrale,
sont des réels, par linéarité de l’intégrale,
![]() ,
,
donc l’application ![]() est linéaire à droite, et comme elle est symétrique, elle est bilinéaire.
est linéaire à droite, et comme elle est symétrique, elle est bilinéaire.
![]() : la fonction intégrée est positive, les bornes sont dans l’ordre croissant, donc
: la fonction intégrée est positive, les bornes sont dans l’ordre croissant, donc ![]() .
.
Si ![]() , comme la fonction intégrée est continue et positive sur
, comme la fonction intégrée est continue et positive sur ![]() , elle est identiquement nulle sur
, elle est identiquement nulle sur ![]() , et comme, pour tout
, et comme, pour tout ![]() ,
,
![]() ,
, ![]() pour tout
pour tout ![]() de
de ![]() , donc
, donc ![]() .
.
Donc ![]() est définie positive.
est définie positive.
Donc ![]() est un produit scalaire.
est un produit scalaire.
Question 4 :
On calcule: ![]() .
.
(On peut aussi calculer directement cette intégrale en intégrant par parties).
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Exercice 4 : Matrices commutantes
Pour ![]() , on désigne par
, on désigne par ![]() l’espace vectoriel
l’espace vectoriel ![]() des polynômes à coefficients réels de degré inférieur ou égal à
des polynômes à coefficients réels de degré inférieur ou égal à ![]() .
.
On donne ![]() réels
réels ![]() , non nécessairement distincts, et pour
, non nécessairement distincts, et pour ![]() ,
, ![]() appartenant à
appartenant à ![]() , on pose
, on pose
![]() =
=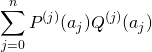 .
.
Question 1 :
L’application ![]() est bien définie sur
est bien définie sur ![]() , à valeurs réelles, puisque des polynômes admettent des dérivés de tout ordre.
, à valeurs réelles, puisque des polynômes admettent des dérivés de tout ordre.
Pour tous ![]() et
et ![]() de
de ![]() ,
, ![]() , donc cette application est symétrique.
, donc cette application est symétrique.
Question 2 :
Pour tout ![]() et
et ![]() de
de ![]() ,
, ![]() est égal à
est égal à ![]() si
si ![]() , et vaut
, et vaut ![]() si
si ![]() .
.
Si ![]() et si
et si ![]() , alors
, alors ![]() dès que
dès que ![]() , et si
, et si ![]() ,
, ![]() ,
,
donc ![]() . Comme
. Comme ![]() ,
, ![]() , donc
, donc ![]() .
.
Donc la base canonique de ![]() est orthogonale pour ce produit scalaire.
est orthogonale pour ce produit scalaire.
Question 3 :
Pour tout ![]() ,
, ![]() , donc
, donc ![]() est de norme
est de norme ![]() .
.
Donc ![]() est une base orthonormée de
est une base orthonormée de ![]() .
.
Pour tout ![]() de
de ![]() , on a:
, on a: 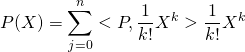 . Comme
. Comme ![]() pour
pour ![]() ,
,
![]() , donc
, donc 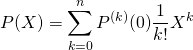 .
.
On retrouve l’expression de ![]() obtenue à l’aide de la formule de Taylor pour les polynômes.
obtenue à l’aide de la formule de Taylor pour les polynômes.
Exercice 5 : Base orthonormée de 
Pour ![]() et
et ![]() appartenant à
appartenant à ![]() , on pose:
, on pose:
![]()
=![]()
+![]()
Question 1 :
![]() est de la forme
est de la forme ![]() , donc
, donc ![]() est bilinéaire et, si
est bilinéaire et, si ![]() et
et ![]() sont les matrices
sont les matrices
(colonnes) de ![]() et
et ![]() dans la base canonique,
dans la base canonique, ![]() où
où 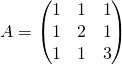 .
.
La matrice ![]() est symétrique, donc
est symétrique, donc ![]() est symétrique.
est symétrique.
Pour tout ![]() de
de ![]() ,
,
![]()
=![]()
=![]()
+![]()
=![]() ,
,
Donc ![]() .
.
Si ![]() , alors
, alors ![]() et
et ![]() , donc
, donc ![]() .
.
Donc ![]() est définie positive.
est définie positive.
Donc ![]() est un produit scalaire.
est un produit scalaire.
Question 2 :
La matrice de ![]() n’est pas diagonale: si
n’est pas diagonale: si ![]() est la base canonique de
est la base canonique de ![]() , on a par exemple
, on a par exemple ![]() ;
;
donc la base canonique n’est pas orthogonale pour ce produit scalaire.
On construit une b.o.n. ![]() en utilisant le procédé de Schmidt:
en utilisant le procédé de Schmidt: ![]() ;
;
![]()
=![]() et
et ![]()
=![]()
=![]() ,
,
Donc ![]() ;
;
![]()
=![]()
=![]() et
et ![]()
=![]() ,
,
Donc ![]() .
.
Boostez vos révisions de maths en ECS2 avec tous les cours en ligne de maths en ECS2 entièrement gratuits :

