Chapitres Maths en ECS2
Corrigés d’exercices : Espaces vectoriels, matrices en ECS2
Résumé de cours Exercices Corrigés
Cours en ligne de Maths en ECS2
Corrigés – Algèbre linéaire ECS2
Exercice 1 : Calcul de 
Soit a est un réel de ![]() , et
, et 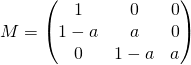 .
.
On note ![]() l’endomorphisme de
l’endomorphisme de ![]() dont la matrice dans la base canonique
dont la matrice dans la base canonique ![]() de
de ![]() est
est ![]() .
.
Question 1 :
Si ![]() comme
comme ![]() est libre,
est libre, ![]() ,
, ![]() ,
, ![]() ,
,
donc ![]() . Donc,
. Donc, ![]() est une famille libre. Cette famille a
est une famille libre. Cette famille a ![]() éléments et
éléments et ![]() ,
,
donc c’est une base de ![]() .
.
Les colonnes de ![]() sont les matrices de
sont les matrices de ![]() ,
, ![]() ,
, ![]() dans
dans ![]() , donc
, donc ![]() ,
,
![]() ,
,
![]() , donc
, donc 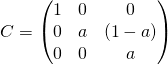 .
.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Question 2 :
Par récurrence, pour ![]() ,
, 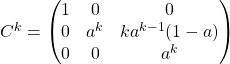 .
.
Question 3 :
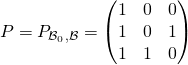 ;
; ![]() . Si
. Si ![]() ,
, ![]() ,
, ![]() , alors
, alors ![]() ,
, ![]() ,
, ![]() , donc
, donc 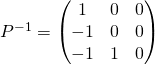 .
.
Comme ![]() , pour
, pour ![]() ,
, ![]() , ce qui donne:
, ce qui donne:
![]() =
=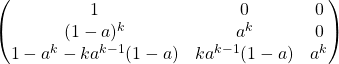
Exercice 2 : Rang et base
On considère l’application :
![]() ,(
,(![]() ).
).
Question 1 :
L’application ![]() est linéaire, donc
est linéaire, donc ![]() est un sous-espace vectoriel de
est un sous-espace vectoriel de ![]() , donc c’est
, donc c’est ![]() ou
ou ![]() .
.
Pour ![]() , la matrice
, la matrice ![]() a pour trace
a pour trace ![]() , donc
, donc ![]() , donc
, donc ![]() .
.
D’après le théorème du rang,
![]() , donc
, donc ![]() .
.
Question 2 :
On utilise la base canonique ![]() de
de ![]() . Si
. Si ![]() ,
,
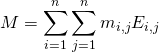 ,
, ![]()
appartient à ![]() si et seulement si
si et seulement si 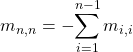 , c’est-à-dire si et seulement si
, c’est-à-dire si et seulement si
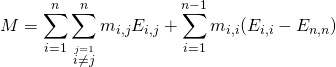
La famille des ![]() ,
, ![]() et
et ![]() ;
;![]() ,
, ![]() est donc une
est donc une
famille génératrice de ![]() . Elle comporte
. Elle comporte ![]() éléments. Donc, c’est une base de
éléments. Donc, c’est une base de ![]() .
.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Exercice 3 : Les matrices telles que 
On note ![]() .
.
Alors ![]() , où pour tous
, où pour tous ![]() et
et ![]() tels que
tels que
![]() et
et
![]() ,
, ![]() .
.
La matrice ![]() appartient à
appartient à ![]() et
et
![]()
=![]()
=![]()
Donc ![]() si et seulement tous les
si et seulement tous les ![]() sont nuls, c’est-à-dire si et seulement si
sont nuls, c’est-à-dire si et seulement si ![]() .
.
Tous les chapitres de maths au programme d’ECS2 sont également proposés gratuitement sur notre site, comme :

