Cours en ligne Physique en Maths Sup
Chapitres Physique en MPSI, PCSI, MP2I, PTSI
Exercices corrigés : La propagation en maths Sup
Résumé de cours Exercices et corrigés
Cours en ligne de physique en Maths Sup
La compréhension de la propagation occupe une place essentielle dans les programmes de MPSI, PTSI, PCSI, où l’étude des phénomènes de propagation constitue un élément clé pour appréhender les diverses applications mathématiques et physiques liées à ce domaine. Si vous aspirez à exceller en physique chimie, nos cours particuliers en physique chimie sont disponibles pour vous soutenir.
En faisant appel à nos services, vous aurez l’opportunité de renforcer votre niveau en physique chimie, de développer votre autonomie et d’améliorer votre méthodologie d’apprentissage. Notre objectif est de vous accompagner dans votre parcours scolaire en maths sup afin de vous aider à exceller et à progresser dans cette discipline.
Exercices corrigés : Signaux et spectres associés, onde progressive
Plan des exercices sur la propagation :
A. Signaux et spectres associés
B. Onde progressive
COURS PARTICULIERS DE PHYSIQUE
Nous avons recruté pour vous les meilleurs profs de physique.
POUR M'AMÉLIORER EN PHYSIQUE, JE CHERCHE DES
Avis Google France ★★★★★ 4,9 sur 5
A. Signaux et spectres associés
Ex. 1 Somme et produit de deux signaux.
On considère les deux signaux
![]()
et ![]()
avec ![]() et
et ![]() .
.
1. Donner l’amplitude, la fréquence et la phase de chacun des deux signaux.
2. Dresser les spectres en amplitude et en phase.
3. On réalise un signal égal à la somme des deux signaux : ![]() . Est-ce un signal sinusoïdal ?
. Est-ce un signal sinusoïdal ?
Est-ce un signal périodique ? Dresser son spectre en amplitude.
4. On réalise un signal proportionnel au produit des deux signaux : ![]() .
.
a. ![]() est une constante. Pourquoi son unité est-elle l’inverse de celle de
est une constante. Pourquoi son unité est-elle l’inverse de celle de ![]() ?
?
b. On donne ![]() .
. ![]() forme-t-il un signal sinusoïdal ? Forme-t-il un signal périodique ? Dresser ses spectres en amplitude et en phase.
forme-t-il un signal sinusoïdal ? Forme-t-il un signal périodique ? Dresser ses spectres en amplitude et en phase.
Correction :
1. On doit transformer le sinus en cosinus : ![]()
et ![]()
Donc ![]() en amplitude,
en amplitude, ![]() et
et ![]() en phase.
en phase.
2. On en déduit les spectres de ![]() et de
et de ![]() un unique bâton en amplitude et un en phase.
un unique bâton en amplitude et un en phase.
3. La somme des deux sinus fait apparaître deux composantes harmoniques, de fréquences ![]() et
et ![]() , alors qu’une fonction sinusoïdale n’en possède qu’une seule, donc le signal somme n’est pas sinusoïdal.
, alors qu’une fonction sinusoïdale n’en possède qu’une seule, donc le signal somme n’est pas sinusoïdal.
Il est en revanche périodique de période ![]()
Son spectre en amplitude est la superposition des deux spectres.
4. a. Pour que la relation soit homogène, il faut que ![]() soit homogène à
soit homogène à ![]() (ou à
(ou à ![]() ) donc que
) donc que ![]() soit sans dimension ; or l’unité de
soit sans dimension ; or l’unité de ![]() est celle de
est celle de ![]() donc
donc ![]() .
.
b. En posant ![]() et
et ![]() , on a
, on a ![]()
![]()
soit ![]()
![]()
On a donc deux composantes harmoniques de fréquences ![]() et
et ![]() et de même amplitude
et de même amplitude ![]() .
.
Ce n’est donc pas un signal sinusoïdal, mais il est périodique de période ![]() . On en déduit les spectres.
. On en déduit les spectres.
Ex. 2 Déformation du spectre.
Une onde progressive dans le sens des ![]() croissants provoque un signal en un point d’abscisse
croissants provoque un signal en un point d’abscisse ![]() dont le spectre fait apparaître deux fréquences
dont le spectre fait apparaître deux fréquences ![]() et
et ![]()
1. Lors de la propagation, Il y a atténuation de l’onde de fréquence ![]() mais pas atténuation de celle de fréquence
mais pas atténuation de celle de fréquence ![]() .
.
Les spectres en amplitude et en phase du signal détecté en ![]() varient-il quand
varient-il quand ![]() augmente ? Peut-on trouver une valeur de
augmente ? Peut-on trouver une valeur de ![]() pour laquelle le spectre est le même qu’en
pour laquelle le spectre est le même qu’en ![]() ?
?
2. Lors de la propagation, la célérité ![]() de l’onde de fréquence
de l’onde de fréquence ![]() est différente de celle
est différente de celle ![]() de fréquence
de fréquence ![]() .
.
Les spectres en amplitude et en phase du signal détecté en ![]() varient-il quand
varient-il quand ![]() augmente ?
augmente ?
Peut-on trouver une valeur de ![]() pour laquelle le spectre est le même qu’en
pour laquelle le spectre est le même qu’en ![]() ?
?
COURS DE PHYSIQUE-CHIMIE
Nous avons sélectionné pour vous les meilleurs profs particuliers.
POUR ACCÉLÉRER MA PROGRESSION EN PHYSIQUE-CHIMIE, JE TROUVE DES
Avis Google France ★★★★★ 4,9 sur 5
B. Ondes progressives
Ex. 1. Analyse graphique d’un soliton.
Voici la photographie d’une corde vibrante à la date ![]()
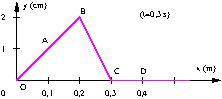
L’onde ![]() se propage dans le sens des
se propage dans le sens des ![]() croissants et a été généré en
croissants et a été généré en ![]() à partir de
à partir de ![]() .
.
1. Que peut signifier le terme « soliton » ?
2. Peut-on définir la longueur d’onde du signal ?
3. Quelle est la célérité de l’onde ?
4. Tracer l’histoire du point ![]() , c’est-à-dire
, c’est-à-dire ![]() en fonction de
en fonction de ![]() .
.
Correction :
1. C’est un paquet d’onde solitaire.
2. L’onde ne possède pas de périodicité spatiale, on peut juste définir son extension spatiale ![]()
3. Le front d’onde, en C sur la photo, a parcouru ![]() en
en ![]() donc
donc ![]()
4. Le front d’onde doit parcourir 0,1 mètres pour arriver en D, donc l’histoire de D commencera 0,1 s après la photographie, donc à ![]()
Par le même raisonnement, le sommet de l’onde arrivera à ![]() et la fin de l’onde à
et la fin de l’onde à ![]() .
.
On en déduit le graphe demandé, et on remarque que la forme des graphes spatial et temporel sont inversés.
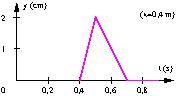
Ex 2. Expression d’une onde progressive sinusoïdale.
Une onde sonore de surpression d’amplitude ![]() , de fréquence
, de fréquence ![]() se propage dans l’air à la célérité
se propage dans l’air à la célérité ![]() , et sa phase en
, et sa phase en ![]() est nulle.
est nulle.
1. Donner l’expression mathématique de l’onde ![]()
2. La puissance acoustique surfacique transportée par l’onde vaut ![]() avec
avec ![]()
a. Quelle est l’unité de ![]() ?
?
b. La valeur moyenne dans le temps d’un cosinus carré vaut 1/2. Calculer la puissance surfacique moyenne.
c. Quelle est la puissance acoustique reçue par le tympan d’un auditeur d’aire ![]() ?
?
Ex 3. Phénomène de dispersion.
Un signal électrique est appliqué en ![]() d’abscisse nulle sur une ligne électrique
d’abscisse nulle sur une ligne électrique ![]() .
.
Le signal ![]() de la tension en
de la tension en ![]() . a l’allure de la première figure ci-dessous.
. a l’allure de la première figure ci-dessous.
Chacune des deux composantes harmoniques du signal en ![]() génère une onde électrique progressive sinusoïdale, mais leurs célérités sont différentes.
génère une onde électrique progressive sinusoïdale, mais leurs célérités sont différentes.
* Celle de fréquence ![]() a une célérité
a une célérité ![]()
une amplitude ![]() et une phase nulle.
et une phase nulle.
*Celle de fréquence ![]() a une célérité
a une célérité ![]()
une amplitude ![]() et une phase nulle.
et une phase nulle.
1. Déterminer la valeur numérique de la fréquence ![]() .
.
2. Donner l’expression mathématique de la tension ![]() en
en ![]() en fonction de
en fonction de ![]() en l’exprimant sous la forme de
en l’exprimant sous la forme de
la somme de ses deux composantes harmoniques.
3. Justifier que ![]()
![]()
4. On se place en ![]() et on relève le signal donné sur la seconde figure
et on relève le signal donné sur la seconde figure
Pourquoi la forme du signal est-elle modifiée par rapport à celle en ![]() ?
?
5. ![]() est-elle la fonction d’une onde progressive ?
est-elle la fonction d’une onde progressive ?
6. Déterminer la valeur numérique d’une abscisse ![]() à laquelle le signal est identique à celui en
à laquelle le signal est identique à celui en ![]() .
.
Si vous souhaitez approfondir vos révisions facilement chez vous consultez l’ensemble des cours en ligne de physique en Maths Sup, dont en voici quelques exemples :

