Chapitres Maths en ECS2
Exercices : Introduction aux fonctions de n variables en ECS2
Résumé de cours Exercices Corrigés
Cours en ligne de Maths en ECS2
Exercices – Introduction aux fonctions de n variables
Exercice 1 :
On donne la fonction ![]() de
de ![]() dans
dans ![]() définie par
définie par ![]() .
.
Question 1 :
Montrer que ![]() est continue sur
est continue sur ![]() .
.
Question 2 :
Montrer que ![]() admet un maximum et un minimum sur
admet un maximum et un minimum sur ![]() , et préciser en quels points ils sont atteints.
, et préciser en quels points ils sont atteints.
Question 3 :
Quelle est la ligne de niveau ![]() de
de ![]() ?
?
Exercice 2 :
On considère la fonction ![]() définie par
définie par ![]() .
.
Question 1 :
Montrer que ![]() est continue sur
est continue sur ![]() .
.
Question 2 :
Montrer que, pour tous réels ![]() ,
, ![]() (on pourra remarquer que, pour tout
(on pourra remarquer que, pour tout ![]() réel,
réel, ![]() ).
).
Question 3 :
Montrer que ![]() si et seulement si
si et seulement si ![]() . Trouver les extrema de
. Trouver les extrema de ![]() et dire en quels ils sont atteints.
et dire en quels ils sont atteints.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Exercice 3 :
Soit ![]() une fonction continue sur
une fonction continue sur ![]() .
.
Dans le plan rapporté à un repère orthonormé ![]() , si
, si ![]() est le point de coordonnées
est le point de coordonnées ![]() , on notera
, on notera ![]() .
.
Question 1 :
Soient ![]() et
et ![]() deux points du plan tels que
deux points du plan tels que ![]() et
et ![]() .
.
Montrer qu’il existe un point ![]() de
de ![]() tel que
tel que ![]() .
.
Question 2 :
Soit ![]() une fonction définie sur
une fonction définie sur ![]() à valeurs réelles, continue sur
à valeurs réelles, continue sur ![]() ; on appelle
; on appelle ![]() sa courbe représentative.
sa courbe représentative.
Montrer que si ![]() et
et ![]() sont deux points de
sont deux points de ![]() de coordonnées
de coordonnées ![]() et
et ![]() tels que
tels que ![]() et
et ![]() , il existe un point
, il existe un point ![]() de
de ![]() , d’abscisse
, d’abscisse ![]() , tel que:
, tel que: ![]() et
et ![]() .
.
Exercice 4 :
Dans le plan muni d’un repère orthonormé ![]() , on donne les points
, on donne les points ![]() ,
, ![]() , et on appelle
, et on appelle ![]() le milieu de
le milieu de ![]() .
.
On considère la fonction ![]() qui à tout point
qui à tout point ![]() associe
associe ![]() , où
, où ![]() .
.
Question 1 :
Calculer ![]() , et montrer que
, et montrer que ![]() .
.
Question 2 :
Quelle est la ligne de niveau ![]() de
de ![]() ? On la notera
? On la notera ![]() .
.
Question 3 :
Donner, pour tout ![]() réel, l’équation de la ligne de niveau
réel, l’équation de la ligne de niveau ![]() de
de ![]() , que l’on notera
, que l’on notera ![]() .
.
Préciser la direction de ![]() , et son intersection avec la droite
, et son intersection avec la droite ![]() .
.
Exercice 5 :
Dans le plan muni d’un repère orthonormé ![]() , on donne
, on donne ![]() points (
points (![]() ,
, ![]() deux à deux distincts, et pour
deux à deux distincts, et pour ![]() , on note
, on note ![]() les coordonnées de
les coordonnées de ![]() .
.
On considère la fonction ![]() qui à tout couple
qui à tout couple ![]() associe
associe 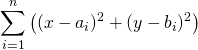 .
.
On notera ![]() le point de coordonnées
le point de coordonnées ![]() , et on pourra donc écrire
, et on pourra donc écrire ![]() .
.
Question 1 :
Montrer que ![]() est continue sur
est continue sur ![]() .
.
La fonction ![]() est-elle majorée ? minorée ?
est-elle majorée ? minorée ?
Question 2 :
Comment peut-on interpréter géométriquement ![]() ?
?
Question 3 :
On suppose dans cette question ![]() .
.
(i) Montrer que ![]() admet un minimum, atteint en un unique point de
admet un minimum, atteint en un unique point de ![]() .
.
(ii) Pour tout réel ![]() , quelle est la ligne de niveau
, quelle est la ligne de niveau ![]() de
de ![]() (on la notera
(on la notera ![]() ) ?
) ?
Question 4 :
On suppose dans cette question ![]() , on note
, on note ![]() le milieu du segment
le milieu du segment ![]() et on pose
et on pose ![]() .
.
(i) En utilisant les vecteurs ![]() ,
, ![]() et
et ![]() , exprimer
, exprimer ![]() à l’aide de
à l’aide de ![]() ,
, ![]() et
et ![]() .
.
(ii) Montrer que ![]() admet un minimum et préciser en quel(s) point(s) il est atteint.
admet un minimum et préciser en quel(s) point(s) il est atteint.
(iii) Pour tout réel ![]() , quelle est la ligne de niveau
, quelle est la ligne de niveau ![]() de
de ![]() ?
?
Question 5 :
On se place dans le cas général ![]() .
.
(i) Montrer que ![]() admet un minimum atteint en un unique point
admet un minimum atteint en un unique point ![]() dont on donnera les coordonnées.
dont on donnera les coordonnées.
(ii) Trouver, pour tout réel ![]() , la ligne de niveau
, la ligne de niveau ![]() de
de ![]() .
.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Exercice 6 :
![]() .
.
Question 1 :
Tracer la ligne de niveau ![]() de
de ![]() dans le plan rapporté à un repère orthonormé
dans le plan rapporté à un repère orthonormé ![]() .
.
Question 2 :
Quels sont les points ![]() de coordonnées
de coordonnées ![]() tels que
tels que ![]() (resp.
(resp. ![]() ) ?
) ?
Question 3 :
(i) Soit ![]() un point distinct de
un point distinct de ![]() .
.
Montrer qu’il existe ![]() et
et ![]() tels que
tels que ![]() et
et ![]() .
.
(ii) Calculer ![]() .
.
(iii) En déduire, pour tout point ![]() ,
, ![]() . Pour quels points
. Pour quels points ![]() a-t-on égalité dans cette inégalité ?
a-t-on égalité dans cette inégalité ?
(iv) Montrer que ![]() admet un maximum quand
admet un maximum quand ![]() décrit
décrit ![]() et dire en quel(s) point(s) ce maximum est atteint.
et dire en quel(s) point(s) ce maximum est atteint.
Question 4 :
En déduire que ![]() admet un maximum sur
admet un maximum sur ![]() et préciser en quels points ce maximum est atteint.
et préciser en quels points ce maximum est atteint.
Pour être parfaitement à jour sur ses connaissances de maths en ECS2, plusieurs cours sont à réviser en parallèle de celui-ci :

