Chapitres Physique-Chimie en Terminale Générale
Cours Lois de Newton terminale générale
Résumé de cours Exercices et corrigés
Cours en ligne de Physique-Chimie en Terminale
Les Lois de Newton constituent un chapitre essentiel à maîtriser pour réussir en terminale. En complément de nos cours particuliers de Physique-Chimie, qui vous aident à progresser, retrouvez les chapitres de Physique-Chimie de terminale, dans nos cours en ligne de terminale en Physique-Chimie ! Vous pouvez également vous entraîner sur les exercices corrigés, pour mieux réussir la Physique-Chimie, qui a un très fort coefficient au bac : voyez combien de points vous devrez gagner pour avoir la mention grâce à notre simulateur du bac. Il est aussi recommandé de prendre des cours de physique chimie si vous rencontrez des difficultés avec les lois de Newton en terminale.
A. Actions mécaniques en terminale générale
1. Définition d’une action mécanique
Une action mécanique (comme par exemple une action mécanique gravitationnelle) est une action susceptible de modifier le mouvement d’un objet. Elle est modélisée par une force représentée par un vecteur :
* il est tracé à partir du point d’application de la force
* sa direction et son sens sont ceux de la force, ceux de l’inflexion du mouvement qu’elle provoque
* sa norme est exprimée en Newton.
2. Force gravitationnelle subie par un corps
La force gravitationnelle est subie par un corps de masse ![]() de la part d’un autre corps massif de masse
de la part d’un autre corps massif de masse ![]() . Si ce corps est un astre (étoile, planète) sphérique de centre
. Si ce corps est un astre (étoile, planète) sphérique de centre ![]() , et si le corps étudié peut être assimilé à un point
, et si le corps étudié peut être assimilé à un point ![]() alors
alors
![]()
avec ![]() et
et ![]() le vecteur unitaire dirigé de
le vecteur unitaire dirigé de ![]() vers
vers ![]()
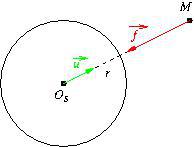
Exemple.
On donne la constante de gravitation
![]()
la masse de la Terre ![]() et son rayon
et son rayon ![]()
Calculer la force gravitationnelle subie par un corps de masse ![]() à la surface de la Terre.
à la surface de la Terre.
Correction : On calcule ![]() , le vecteur force est vertical, dirigé vers le centre de la Terre.
, le vecteur force est vertical, dirigé vers le centre de la Terre.
3. Le poids en tant que force gravitationnelle
Le poids peut être assimilé, en bonne approximation, à la force gravitationnelle subie par un corps à proximité de la surface d’une planète.
Il est vertical, dirigé vers le bas
![]()
avec ![]() ,
,
![]() est la norme du champ de pesanteur, ou accélération de la pesanteur et
est la norme du champ de pesanteur, ou accélération de la pesanteur et ![]() est le vecteur unitaire vertical dirigé vers le haut au point considéré.
est le vecteur unitaire vertical dirigé vers le haut au point considéré.
Pour le poids terrestre, à Paris,
![]()
Exemple.
La masse de la Lune est 81,3 fois plus petite que celle de la Terre, et son rayon 3,66 fois plus petit que celui de la Terre.
Quel est la norme du champ de pesanteur lunaire ?
Correction :
On a
![]()
![]()
donc en faisant le rapport
![]()
![]()
donc ![]()
4. La force électrique subie
La force électrique subie par un corps ponctuel ![]() de charge
de charge ![]() de la part d’un corps immobile de charge
de la part d’un corps immobile de charge ![]() placé en
placé en ![]() est la force de Coulomb
est la force de Coulomb
![]()
avec ![]() et
et ![]() le vecteur unitaire dirigé de
le vecteur unitaire dirigé de ![]() vers
vers ![]()
5. Un corps relié à un fil
Un corps relié à un fil tendu subit de sa part une force de tension, dans la direction du fil, dirigé du corps vers le fil.
6. La force subie par un corps
La force subie par un corps se déplaçant au contact d’un solide se décompose en
* une force normale ![]() orthogonale au suport
orthogonale au suport
* une force tangentielle ![]() parallèle au support, et s’opposant au glissement éventuel du corps : en particulier, si le corps glisse à la vitesse de glissement
parallèle au support, et s’opposant au glissement éventuel du corps : en particulier, si le corps glisse à la vitesse de glissement ![]() par rapport au support, alors
par rapport au support, alors ![]() a même direction, et sens opposé à
a même direction, et sens opposé à ![]()
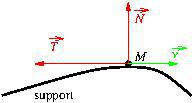
Exemple.
On pose un objet sans vitesse initiale sur un plan incliné.
Déterminer le sens et la direction des vecteurs ![]() et
et ![]() subis par l’objet.
subis par l’objet.
Correction : Si le corps glisse, ce sera vers le bas, donc la force tangentielle est dirigée vers le haut de la pente.
7. La force subie par un corps de la part d’un fluide
La force subie par un corps de la part d’un fluide dans lequel il est plongé se décompose en
* la résultante des forces pressantes (normales) sur sa surface : en particulier, si le corps est immobile, cette résultante s’appelle la poussée d’Archimède
* la résultante des forces tangentielles sur sa surface : elle est nulle si le corps est immobile dans le fluide, et de même direction et de sens opposé au vecteur vitesse de l’objet par rapport au fluide.
COURS DE PHYSIQUE-CHIMIE
Nous avons sélectionné pour vous les meilleurs profs particuliers.
POUR ACCÉLÉRER MA PROGRESSION EN PHYSIQUE-CHIMIE, JE TROUVE DES
Avis Google France ★★★★★ 4,9 sur 5
B. Les composantes d’un vecteur force en terminale
1. Les vecteurs représentent les forces
Les forces étant représentées par des vecteurs, il faut exprimer leurs composantes (ou coordonnées) dans un repère donné, comme on le fait pour les vecteurs position, vitesse et accélération en cinématique.
Exemple.
Un corps ![]() se déplace sur un rail horizontal formant l’axe
se déplace sur un rail horizontal formant l’axe ![]() , et on définit l’axe
, et on définit l’axe ![]() vertical vers le haut.
vertical vers le haut. ![]() subit son poids et la force de contact du rail et se déplace dans le sens des
subit son poids et la force de contact du rail et se déplace dans le sens des ![]() croissants.
croissants.
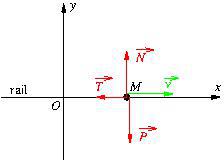
Donner les composantes des vecteurs
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() et
et ![]()
En notant ![]() l’abscisse du point,
l’abscisse du point, ![]() sa masse,
sa masse, ![]() et
et ![]() les normes des vecteurs forces tangentielle et normale.
les normes des vecteurs forces tangentielle et normale.
Correction :
D’après les lois de la cinématique :
![]()
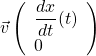
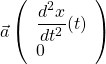
![]()
![]() se déplace vers la droite, sa vitesse de glissement est donc vers la droite donc la force tangentielle de contact est dirigée vers la gauche
se déplace vers la droite, sa vitesse de glissement est donc vers la droite donc la force tangentielle de contact est dirigée vers la gauche
![]()
![]()
2. Exprimer les composantes d’une force
Lorsqu’une force a pour norme ![]() et qu’elle a une direction définie par un angle
et qu’elle a une direction définie par un angle ![]() par rapport à un des axes d’un repère orthonormal à deux dimensions, il existe un moyen pratique d’exprimer ses composantes.
par rapport à un des axes d’un repère orthonormal à deux dimensions, il existe un moyen pratique d’exprimer ses composantes.
* Celles-ci valent ![]() sur un axe, et
sur un axe, et ![]() sur l’autre axe.
sur l’autre axe.
* Les signes s’ajustent à partir du schéma.
* La composante avec ![]() est celle correspondant à l’axe sur lequel l’angle alpha est COllé (comme COsinus).
est celle correspondant à l’axe sur lequel l’angle alpha est COllé (comme COsinus).
Exemple. Quelles sont les composantes du poids dans le schéma suivant ?
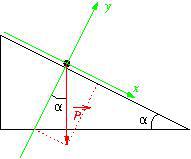
Correction :
* La composante sur ![]() est positive, celle sur
est positive, celle sur ![]() est négative.
est négative.
* L’angle alpha est collé contre l’axe ![]()
On en déduit
![]()
Avis Google France ★★★★★ 4,9 sur 5COURS PARTICULIERS DE PHYSIQUE
Nous avons recruté pour vous les meilleurs profs de physique.
POUR M'AMÉLIORER EN PHYSIQUE, JE CHERCHE DES
C. Lois de Newton, cours de terminale générale
1. La troisième loi de Newton
La troisième loi de Newton énonce que si deux corps ![]() et
et ![]() sont en interaction, la force exercée par l’un sur l’autre est opposée à celle exercée par le second sur le premier
sont en interaction, la force exercée par l’un sur l’autre est opposée à celle exercée par le second sur le premier
![]()
Exemple.
Un fil inextensible, de masse nulle, est tendu entre deux corps ![]() et
et ![]() .
.
En admettant que la norme de la tension du fil est la même en tout point du fil, justifier la troisième loi de Newton dans ce cas.
Correction :
* La force de tension subie par un corps est dirigée selon le fil, les deux forces ont donc même direction.
* La force de tension est dirigée du corps vers le fil, donc les signes des forces sont opposés.
* La norme étant partout la même, les forces sont bien des vecteurs opposés.
2. Le référentiel galiléen
Un référentiel galiléen est un référentiel dans lequel un corps ponctuel qui n’est soumis à aucune force est immobile ou animé d’un mouvement rectiligne uniforme.
Tout référentiel en translation rectiligne uniforme par rapport à un référentiel galiléen est lui-même galiléen.
Le référentiel héliocentrique peut être considéré comme galiléen.
Exemple.
Le référentiel géocentrique a pour centre le centre de la Terre et est en mouvement de translation par rapport au référentiel héliocentrique. Sur quelle durée peut-on l’estimer galiléen ?
Correction :
Il faut que le mouvement du centre de la Terre soit rectiligne uniforme : comme il décrit un cercle autour du Soleil en une année, on peut estimer que sur une durée de 1 jour, il est presque rectiligne.
3. La deuxième loi de Newton
Soit ![]() un corps ponctuel (ou un corps ramené à son centre) de masse
un corps ponctuel (ou un corps ramené à son centre) de masse ![]() , soumis à un ensemble de forces ; dans un référentiel galiléen, la somme vectorielle
, soumis à un ensemble de forces ; dans un référentiel galiléen, la somme vectorielle
![]() qu’il subit est égale au produit de la masse par son vecteur accélération
qu’il subit est égale au produit de la masse par son vecteur accélération
![]()
Exemple.
Un corps ponctuel de masse ![]() est soumis à son seul poids.
est soumis à son seul poids.
a. Quelle est son accélération, en supposant le référentiel terrestre galiléen ?
b. On définit le repère ![]() où
où ![]() est un vecteur unitaire horizontal et
est un vecteur unitaire horizontal et ![]() un vecteur unitaire vertical dirigé vers le haut. On note
un vecteur unitaire vertical dirigé vers le haut. On note ![]() et
et ![]() les coordonnées de
les coordonnées de ![]() à la date
à la date ![]() .
.
À l’instant initial ![]() , on lâche
, on lâche ![]() sans vitesse initiale depuis le point
sans vitesse initiale depuis le point ![]()
Établir les expressions de ![]() et de
et de ![]()
Correction :
Dans le référentiel galiléen terrestre, la deuxième loi de Newton s’écrit
![]()
soit ![]()
donc ![]()
On en déduit
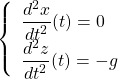
On primitive par rapport au temps
![]()
où ![]() et
et ![]() sont des constantes d’intégration.
sont des constantes d’intégration.
La vitesse initiale étant nulle, on exprime à ![]()
![]()
donc ![]() et
et
![]()
On primitive par rapport au temps
![]()
où ![]() et
et ![]() sont des constantes d’intégration.
sont des constantes d’intégration.
En utilisant la position initiale, on exprime à ![]()
![]()
donc ![]() et
et ![]() et
et
![]()
4. La première loi de Newton
Elle peut être considérée comme un simple cas particulier de la deuxième. Soit ![]() un corps ponctuel (ou un corps ramené à son centre) soumis à un ensemble de forces ; dans un référentiel galiléen,
un corps ponctuel (ou un corps ramené à son centre) soumis à un ensemble de forces ; dans un référentiel galiléen, ![]() est immobile ou en mouvement rectiligne uniforme si et seulement si la somme vectorielle
est immobile ou en mouvement rectiligne uniforme si et seulement si la somme vectorielle ![]() qu’il subit est nulle.
qu’il subit est nulle.
Exemple.
![]() de masse
de masse ![]() est posé sur un plan incliné d’un angle
est posé sur un plan incliné d’un angle ![]() par rapport à l’horizontale. Il est immobile, en équilibre sous l’action des forces
par rapport à l’horizontale. Il est immobile, en équilibre sous l’action des forces ![]() ,
,
![]() et
et ![]() .
.
En travaillant dans le repère ![]() indiqué sur le schéma, exprimer les normes
indiqué sur le schéma, exprimer les normes ![]() et
et ![]() en fonction de
en fonction de ![]() ,
, ![]() et
et ![]() .
.
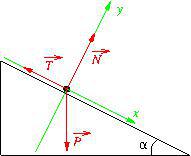
Correction :
On exprime les composantes des trois vecteurs
![]()
![]()
![]()
À l’équilibre dans le référentiel du laboratoire, supposé galiléen, la première loi de Newton donne
![]()
![]()
donc ![]()
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Retrouvez toutes les annales du bac de physique sur les Lois de Newton et le reste du Programme de Physique en Terminale. Ces annales du bac vous permettront de travailler au mieux et de ne pas être déçu le jour des résultats du Bac. Mais avant de vous lancer sur les annales, vérifiez toutes vos connaissances grâce aux cours en ligne de physique-chimie de terminale, par exemple sur ces chapitres :

