Chapitres Physique-Chimie en Terminale Générale
Cours Mécanique Gravitationnelle terminale générale
Résumé de cours Exercices et corrigés
Cours en ligne de Physique-Chimie en Terminale
Découvrez tous les autres chapitres de Physique-Chimie de terminale, dans nos cours en ligne de terminale en Physique-Chimie et avec un prof de physique-chimie ! Cela vous aidera à maîtriser le cours sur la Mécanique Gravitationnelle en terminale générale. Ce sera d’autant plus facile en prenant des cours particuliers de Physique-Chimie. Votre progression vous permettra alors de viser après le bac, des établissements aux bons classements.
A. Satellite en orbite circulaire en terminale
1. Les astres en Terminale générale
Le mot « astre » désignera dans tout ce chapitre un corps massif ![]() (étoile, planète) sphérique, de masse
(étoile, planète) sphérique, de masse ![]() et de centre
et de centre ![]() .
.
Le référentiel astro-centrique (hélio-pour le Soleil, géo- pour la Terre) ![]() est un référentiel galiléen dans lequel
est un référentiel galiléen dans lequel ![]() est un point fixe et dont les axes sont dirigés vers des étoiles lointaines telles que
est un point fixe et dont les axes sont dirigés vers des étoiles lointaines telles que ![]() est galiléen.
est galiléen.
La force de gravitation exercée par ![]() sur un corps lui-même sphérique de centre
sur un corps lui-même sphérique de centre ![]() et de masse
et de masse ![]() est
est
![]()
où ![]()
est la constante de gravitation universelle, ![]() et
et ![]() un vecteur unitaire de même direction et de même sens que
un vecteur unitaire de même direction et de même sens que ![]()
2. Application de la deuxième loi de Newton en Terminale
L’application de la deuxième loi de Newton en terminale à ![]() dans le référentiel astro-centrique s’écrit
dans le référentiel astro-centrique s’écrit
![]()
![]()
donc ![]()
L’accélération ne dépend pas de la masse du corps étudié, ce sera le cas pour de nombreuses autres grandeurs.
COURS DE PHYSIQUE-CHIMIE
Nous avons sélectionné pour vous les meilleurs profs particuliers.
POUR ACCÉLÉRER MA PROGRESSION EN PHYSIQUE-CHIMIE, JE TROUVE DES
Avis Google France ★★★★★ 4,9 sur 5
3. Norme de vitesse et rayon du cercle en Terminale
On suppose que ![]() a un mouvement circulaire de centre
a un mouvement circulaire de centre ![]() et de rayon
et de rayon ![]() constant. On utilise le repère de Frenet.
constant. On utilise le repère de Frenet.
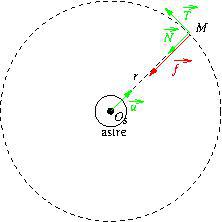
On remarque que le vecteur normal unitaire, dirigé de ![]() vers le centre du cercle, est l’opposé du vecteur
vers le centre du cercle, est l’opposé du vecteur ![]()
![]()
En utilisant les formules de cinématique on en déduit
![]()
* En projection sur ![]() on a
on a
![]()
Le mouvement circulaire est donc uniforme car la norme ![]() de la vitesse est constante.
de la vitesse est constante.
* En projection sur ![]() on a
on a
![]()
On en déduit la relation entre la norme de la vitesse et le rayon du cercle
![]()
4. Quotient du carré de la période par le cube du rayon
![]() a un mouvement circulaire uniforme de centre
a un mouvement circulaire uniforme de centre ![]() , de rayon
, de rayon ![]() , à la vitesse
, à la vitesse ![]() . Il a donc un mouvement périodique. Il effectue un tour, donc une distance
. Il a donc un mouvement périodique. Il effectue un tour, donc une distance ![]() en une durée
en une durée ![]() appelée période de révolution.
appelée période de révolution.
Par définition de la norme de la vitesse
![]()
donc ![]()
et en reprenant l’expression de la vitesse
![]()
On en déduit la troisième loi de Kepler pour les orbites circulaires
![]()
On remarque donc que pour un astre donné (dont on ne connaît pas toujours la masse), tous les satellites en orbite circulaire ont des périodes et des rayons a priori différents, mais le quotient du carré de la période par le cube du rayon est le même pour tous.
5. Satellite géostationnaire en Terminale
Un satellite géostationnaire est un corps ![]() qui reste immobile dans le référentiel terrestre, donc à la verticale du même point
qui reste immobile dans le référentiel terrestre, donc à la verticale du même point ![]() et à la même altitude, sous la seule action de la force de gravitation de la Terre.
et à la même altitude, sous la seule action de la force de gravitation de la Terre.
Le référentiel terrestre est en rotation uniforme autour de l’axe des pôles par rapport au référentiel géocentrique, et il effectue un tour en un jour sidéral (très légèrement différent du jour terrestre)
![]()
Si on plante une aiguille sur le globe terrestre, et qu’on fait tourner celui-ci, on constate que la tête de l’aiguille, représentant le satellite géostationnaire, décrit un cercle, pendant que l’aiguille décrit un cône de révolution.
Voici la figure lorsque ![]() n’est pas sur l’équateur.
n’est pas sur l’équateur.
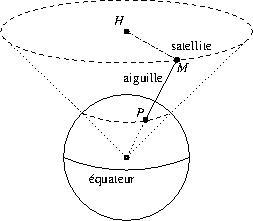
On constate que ![]() a un mouvement circulaire dont le centre
a un mouvement circulaire dont le centre ![]() n’est pas le centre de la Terre, ce qui est en contradiction avec les résultats précédents, car le centre du cercle décrit par un satellite en orbite circulaire est le centre de l’astre.
n’est pas le centre de la Terre, ce qui est en contradiction avec les résultats précédents, car le centre du cercle décrit par un satellite en orbite circulaire est le centre de l’astre.
Un satellite géostationnaire ne peut donc être qu’à la verticale d’un point ![]() sur l’équateur. Il évolue donc dans le plan équatorial.
sur l’équateur. Il évolue donc dans le plan équatorial.
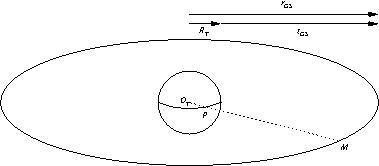
Par application de la troisième loi de Kepler, le rayon du cercle décrit par ![]() autour du centre de la Terre vaut
autour du centre de la Terre vaut
![]()
Le rayon de la Terre au niveau de l’équateur vaut environ
![]()
On en déduit l’altitude du satellite géostationnaire, mesurée depuis le sol
![]()
soit environ 36 000 km d’altitude.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
B. Lois de Kepler en terminale générale
1. Première loi de Kepler en Terminale
Les satellites d’un astre ![]() quelconque de centre
quelconque de centre ![]() évoluent dans le référentiel astrocentrique supposé galiléen en décrivant périodiquement une courbe plane, une ellipse, dont
évoluent dans le référentiel astrocentrique supposé galiléen en décrivant périodiquement une courbe plane, une ellipse, dont ![]() est un des foyers.
est un des foyers.
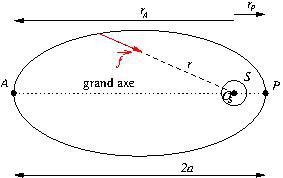
Une ellipse peut être décrite comme un pseudo-cercle dont le rayon varie
* d’une valeur minimale ![]() au point
au point ![]() de la trajectoire le plus proche de
de la trajectoire le plus proche de ![]() , le périastre (périhélie si l’astre est le Soleil, périgée si c’est la Terre)
, le périastre (périhélie si l’astre est le Soleil, périgée si c’est la Terre)
* jusqu’à une valeur maximale ![]() au point
au point ![]() de la trajectoire le plus éloigné de
de la trajectoire le plus éloigné de ![]() , l’apastre (aphélie si l’astre est le Soleil, apogée si c’est la Terre).
, l’apastre (aphélie si l’astre est le Soleil, apogée si c’est la Terre).
![]() ,
, ![]() et
et ![]() sont alignés et le segment
sont alignés et le segment ![]() forme le grand axe de l’ellipse, sa longueur est notée
forme le grand axe de l’ellipse, sa longueur est notée ![]() , où
, où
![]() est appelé le « demi-grand » axe, c’est le rayon moyen de la trajectoire autour de
est appelé le « demi-grand » axe, c’est le rayon moyen de la trajectoire autour de ![]() .
.
2. Deuxième loi de Kepler en Terminale
Imaginons qu’on tende une corde entre ![]() et
et ![]() .
.
Lorsque ![]() se déplace, cette corde balaie l’espace qui les sépare.
se déplace, cette corde balaie l’espace qui les sépare.
La deuxième loi, appelée « loi des aires », énonce que le segment ![]() balaie des surfaces égales pendant des durées égales, donc que la « vitesse aréolaire », vitesse de balayage exprimée en mètres carrés par seconde, est constante.
balaie des surfaces égales pendant des durées égales, donc que la « vitesse aréolaire », vitesse de balayage exprimée en mètres carrés par seconde, est constante.
Méthode sur la 2eme loi de Kepler :
Cette loi des aires est souvent oubliée par les élèves alors qu’elle permet souvent de donner rapidement, sans aucun calcul, une réponse à une question qualitative relative à la vitesse de ![]() , qui n’est pas constante, contrairement à ce qui se passe dans le cas du satellite en orbite circulaire.
, qui n’est pas constante, contrairement à ce qui se passe dans le cas du satellite en orbite circulaire.
3. Troisième loi de Kepler en Terminale
On généralise la loi établie dans le cas de l’orbite circulaire au cas général de l’orbite elliptique, en remplaçant le rayon du cercle par le demi-grand axe
![]() est une valeur constante pour tous les satellites d’un même astre.
est une valeur constante pour tous les satellites d’un même astre.
Remarquons que pour les satellites en orbite circulaire, le demi-grand axe est égal au rayon, et la constante est donc celle qu’on avait trouvée dans ce cas.
On peut donc écrire
![]()
Mais dans le respect du programme, cette expression de la constante n’est pas exigible.
Retrouvez toutes les annales du bac de physique-chimie et plus généralement toutes les annales du bac en Terminale pour vous entraîner au mieux afin d’être fiers de vos résultats au bac le moment venu. Travailler la physique chimie en terminale est particulièrement utile, étant donné son fort coefficient au bac. Vérifiez donc votre niveau de connaissances sur les chapitres au programme, comme :

