Chapitres Physique-Chimie en Terminale Générale
Cours Cinématique terminale générale
Résumé de cours Exercices et corrigés
Cours en ligne de Physique-Chimie en Terminale
La réussite au baccalauréat nécessite de maîtriser le cours sur la Cinématique en terminale générale, quitte à prendre des cours particuliers de Physique-Chimie en cas de lacunes. Retrouvez les autres chapitres de Physique-Chimie de terminale, dans nos cours en ligne de terminale en Physique-Chimie ! Ils vous seront utiles pour maîtriser la Physique-Chimie qui a un fort coefficient au bac, comme vous pouvez le vérifier sur notre simulateur du bac. N’hésitez pas à prendre des cours de physique chimie pour exceller en cinématique !
A. Le vecteur position en terminale générale
1. Un référentiel est un solide
On peut en extraire un point origine ![]() , et trois vecteurs non coplanaires
, et trois vecteurs non coplanaires ![]() .
.
![]() forme alors lui-même un référentiel.
forme alors lui-même un référentiel.
Si les trois vecteurs sont deux à deux orthogonaux, et de norme 1, on les note avec des minuscules et
![]() forme un référentiel orthonormal.
forme un référentiel orthonormal.
Exemple
Le référentiel terrestre est lié à la Terre. Définir deux référentiels orthonormaux distincts, l’un de centre un point ![]() du sol terrestre, et un de centre confondu avec le centre
du sol terrestre, et un de centre confondu avec le centre ![]() de la Terre.
de la Terre.
Correction :
* En ![]() , on peut définir trois vecteurs de norme 1 :
, on peut définir trois vecteurs de norme 1 : ![]() dirigé vers le Nord,
dirigé vers le Nord, ![]() dirigé vers l’ouest et
dirigé vers l’ouest et ![]() vertical dirigé vers le haut.
vertical dirigé vers le haut.
![]() forme un référentiel terrestre orthonormal.
forme un référentiel terrestre orthonormal.
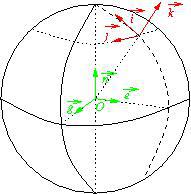
* Autour de ![]() , on peut définir trois vecteurs de norme 1 :
, on peut définir trois vecteurs de norme 1 : ![]() dirigé vers le pôle Nord,
dirigé vers le pôle Nord, ![]() dirigé vers le point équatorial du méridien de Greenwich et
dirigé vers le point équatorial du méridien de Greenwich et ![]() dirigé vers le point de l’équateur du méridien 90° est (il passe au milieu du golfe du Bengale).
dirigé vers le point de l’équateur du méridien 90° est (il passe au milieu du golfe du Bengale).
![]() forme un référentiel terrestre orthonormal.
forme un référentiel terrestre orthonormal.
2. Le vecteur position en Terminale
Le vecteur position est le vecteur qui définit la position d’un point mobile ![]() à une date
à une date ![]() donnée.
donnée.
Dans le référentiel (orthonormal) ![]() , on peut écrire
, on peut écrire
![]()
On peut alors écrire
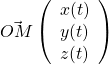
Exemple
Si ![]() est un point du sol terrestre, dans le repère terrestre orthonormal terrestre
est un point du sol terrestre, dans le repère terrestre orthonormal terrestre ![]() , où
, où ![]() est un vecteur vertical dirigé vers le haut, quels noms donne-t-on aux coordonnées
est un vecteur vertical dirigé vers le haut, quels noms donne-t-on aux coordonnées ![]() ,
, ![]() et
et ![]() ?
?
Correction : ![]() est l’abscisse,
est l’abscisse, ![]() l’ordonnée et
l’ordonnée et ![]() la cote ou l’altitude.
la cote ou l’altitude.
COURS DE PHYSIQUE CHIMIE
Gagner en autonomie avec les meilleurs profs
Des cours de grande qualité
Avis Google France ★★★★★ 4,9 sur 5
B.Vecteurs vitesse et accélération en terminale
1. Le vecteur vitesse en Terminale
Le vecteur vitesse a pour direction la tangente à la trajectoire, pour sens celui du déplacement du point ![]() étudié, pour norme la vitesse instantanée de
étudié, pour norme la vitesse instantanée de ![]() , exprimée en
, exprimée en ![]()
Il est égal à la dérivée par rapport au temps du vecteur position ![]()
![]()
Dans le repère ![]() associé au référentiel d’étude, ses coordonnées sont égales aux dérivées par rapport au temps des coordonnées de
associé au référentiel d’étude, ses coordonnées sont égales aux dérivées par rapport au temps des coordonnées de ![]()
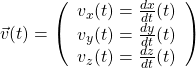
Exemple
a. Déterminer le vecteur vitesse pour le point ![]() dont le mouvement est défini par les équations horaires
dont le mouvement est défini par les équations horaires
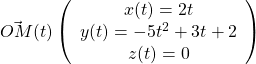
b. Calculer la norme de la vitesse à l’instant ![]()
Correction :
a. On calcule les dérivées
![]()
![]()
![]()
donc 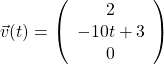
b. On calcule
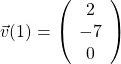
donc ![]()
soit ![]()
2. Le vecteur accélération en Terminale
Le vecteur accélération a pour direction et sens ceux de l’inflexion du vecteur vitesse, et pour norme l’accélération instantanée de ![]() , exprimée en
, exprimée en ![]()
Pour comprendre le sens physique de l’accélération, on peut l’exprimer en « mètres par seconde par seconde ». Ainsi, l’accélération de la pesanteur, qui est en particulier celle d’un mobile qu’on laisse chuter verticalement, vaut environ 10 mètres par seconde par seconde, soient ![]() par seconde. On en déduit que lors de la chute libre verticale d’un mobile, sa vitesse augmente de
par seconde. On en déduit que lors de la chute libre verticale d’un mobile, sa vitesse augmente de ![]() chaque seconde. Si sa vitesse est nulle à l’instant initial, elle vaut (en négligeant les frottements)
chaque seconde. Si sa vitesse est nulle à l’instant initial, elle vaut (en négligeant les frottements) ![]() au bout d’une seconde,
au bout d’une seconde, ![]() au bout de deux secondes,
au bout de deux secondes, ![]() au bout de trois secondes, etc.
au bout de trois secondes, etc.
Il est égal à la dérivée par rapport au temps du vecteur vitesse ![]() , donc à la dérivée seconde de
, donc à la dérivée seconde de ![]()
![]()
Dans le repère ![]() associé au référentiel d’étude, ses coordonnées sont égales aux dérivées par rapport au temps des coordonnées de
associé au référentiel d’étude, ses coordonnées sont égales aux dérivées par rapport au temps des coordonnées de ![]() , donc aux dérivées secondes de
, donc aux dérivées secondes de ![]()
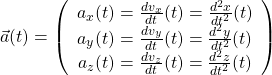
Exemple
Déterminer le vecteur accélération pour le point ![]() dont le mouvement est défini par les équations horaires (cf. exemple précédent)
dont le mouvement est défini par les équations horaires (cf. exemple précédent)
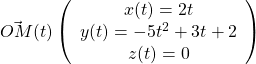
Correction :
On a déjà établi que 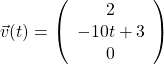
On en déduit que 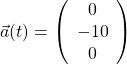
3. Construction graphique en Terminale
On dispose d’un chronogramme, c’est-à-dire d’un document graphique donnant les positions successives de ![]() à des dates régulièrement espacées,
à des dates régulièrement espacées,
![]() ,
, ![]() ,
, ![]() , …,
, …, ![]() , … où
, … où![]() est une durée (le pas temporel du chronogramme) et
est une durée (le pas temporel du chronogramme) et ![]() un nombre entier naturel.
un nombre entier naturel.
Pour ![]() , on obtient une bonne estimation du vecteur vitesse à la date
, on obtient une bonne estimation du vecteur vitesse à la date ![]() par
par
![]()
soit ![]()
Voici le procédé de construction.
* On construit le vecteur ![]() joignant les points avant et après
joignant les points avant et après ![]()
* Sa direction et son sens sont ceux du vecteur vitesse ![]()
On mesure la norme du vecteur ![]() , celle du vecteur vitesse est égale à
, celle du vecteur vitesse est égale à
![]()
On calcule cette norme.
* On choisit une échelle de représentation graphique ![]()
* On trace le vecteur vitesse à partir de ![]() avec la direction, le sens, et la longueur donnée par l’échelle choisie.
avec la direction, le sens, et la longueur donnée par l’échelle choisie.
On procède de même pour tracer une estimation du vecteur accélération.
![]()
Exemple
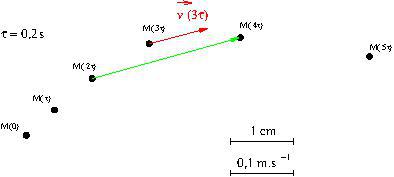
Sur le document suivant, pour déterminer ![]() , on construit le vecteur
, on construit le vecteur ![]() , il mesure environ 2,4 cm, on en déduit que
, il mesure environ 2,4 cm, on en déduit que
![]()
On construit donc à l’échelle un vecteur d’environ 1,2 cm, à partir du point ![]() , parallèle et de même sens que
, parallèle et de même sens que ![]()
COURS DE PHYSIQUE
Trouvez le professeur parfait de physique
Là pour vous guider, quel que soit votre niveau scolaire
Avis Google France ★★★★★ 4,9 sur 5
C. Étude du mouvement rectiligne en terminale
Un point ![]() a un mouvement rectiligne s’il se déplace sur une droite, donc si sa trajectoire forme un segment de droite.
a un mouvement rectiligne s’il se déplace sur une droite, donc si sa trajectoire forme un segment de droite.
Il est alors naturel de choisir un point ![]() origine sur cette droite et de nommer
origine sur cette droite et de nommer ![]() ,
, ![]() ou
ou ![]() le référentiel d’étude selon cette droite orientée.
le référentiel d’étude selon cette droite orientée.
![]() a un mouvement est rectiligne uniforme si son vecteur vitesse
a un mouvement est rectiligne uniforme si son vecteur vitesse ![]() est constant, ou de façon équivalente si son vecteur accélération
est constant, ou de façon équivalente si son vecteur accélération ![]() est nul.
est nul.
Pour un mouvement selon l’axe ![]() , on en déduit
, on en déduit
![]()
![]()
![]()
où ![]() est la vitesse algébrique (constante) et
est la vitesse algébrique (constante) et ![]() l’abscisse à l’instant initial
l’abscisse à l’instant initial ![]()
Exemple
Un mobile ![]() se déplace sur l’axe
se déplace sur l’axe ![]() a pour équation horaire
a pour équation horaire
![]()
a. Vérifier que c’est un mouvement rectiligne uniforme.
b. Quelle est sa vitesse ? Commenter son signe.
c. Calculer son abscisse initiale ![]()
d. Calculer la date à laquelle ![]()
Correction :
a. On a
![]() = constante
= constante
![]()
b. ![]() donc le mouvement se fait dans le sens des
donc le mouvement se fait dans le sens des ![]() décroissants, à une vitesse de norme
décroissants, à une vitesse de norme
![]()
c. ![]()
d. ![]()
soit ![]()
2. Un point  a un mouvement rectiligne
a un mouvement rectiligne
Ce mouvement est rectiligne accéléré (on devrait dire « rectiligne uniformément accéléré ») si son vecteur accélération ![]() est constant, selon l’axe du mouvement.
est constant, selon l’axe du mouvement.
Pour un mouvement selon l’axe ![]() , on en déduit
, on en déduit
![]()
![]()
![]()
où ![]() est l’accélération algébrique (constante),
est l’accélération algébrique (constante), ![]() la vitesse algébrique et
la vitesse algébrique et ![]() l’abscisse à l’instant initial
l’abscisse à l’instant initial ![]()
Démonstration de cours : Établir les expressions de ![]() et de
et de ![]()
* On a par définition
![]()
donc en primitivant
![]()
où ![]() est une constante.
est une constante.
À l’instant initial ![]() on en déduit
on en déduit
![]()
donc ![]()
* On a par définition
![]()
donc en primitivant
![]()
où ![]() est une constante.
est une constante.
À l’instant initial ![]() on en déduit
on en déduit
![]()
donc ![]()
1. Le mouvement circulaire en Terminale
![]() a un mouvement est circulaire si sa trajectoire est un arc de cercle de centre
a un mouvement est circulaire si sa trajectoire est un arc de cercle de centre ![]() et rayon
et rayon ![]() .
.
Le mouvement est circulaire et uniforme si la norme ![]() de sa vitesse est constante.
de sa vitesse est constante.
ATTENTION ! Ce n’est pas le vecteur vitesse qui est constant, donc l’accélération du point ![]() n’est pas nulle.
n’est pas nulle.
Lorsque ![]() fait un tour complet du cercle, il parcourt une distance égale au périmètre du cercle
fait un tour complet du cercle, il parcourt une distance égale au périmètre du cercle ![]() . La durée de parcours est la période
. La durée de parcours est la période ![]() du mouvement.
du mouvement.
On a donc
![]() ou
ou ![]()
Exemple
Le centre de la Terre décrit un mouvement à peu près circulaire et uniforme autour du centre du Soleil, de rayon ![]() avec une période égale à une année terrestre, soit 365,25 jours. Calculer la norme de la vitesse.
avec une période égale à une année terrestre, soit 365,25 jours. Calculer la norme de la vitesse.
Correction :
On convertit ![]() en secondes :
en secondes :
![]()
![]()
On en déduit
![]()
2. La description cinématique en Terminale
La description cinématique (vecteurs position, vitesse, accélération) d’un mouvement circulaire n’est pas aisée dans un référentiel (référentiel « cartésien ») ![]()
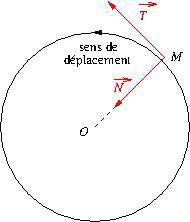
On préfère travailler en utilisant le repère de Frenet défini ainsi :
à une date ![]() ,
, ![]() se trouve en un point du cercle et tourne dans un sens donné
se trouve en un point du cercle et tourne dans un sens donné
* le vecteur tangent ![]() est un vecteur de norme 1, tangent au cercle et orienté dans le sens du déplacement
est un vecteur de norme 1, tangent au cercle et orienté dans le sens du déplacement
* le vecteur normal ![]() est un vecteur de norme 1, perpendiculaire dans le plan du cercle au vecteur
est un vecteur de norme 1, perpendiculaire dans le plan du cercle au vecteur ![]() et orienté vers le centre
et orienté vers le centre ![]() du cercle.
du cercle.
3. Mouvement circulaire et vitesse en Terminale
Un point ![]() en mouvement circulaire, de centre
en mouvement circulaire, de centre ![]() , de rayon
, de rayon ![]() , a pour vitesse
, a pour vitesse ![]() , constante si le mouvement est circulaire uniforme, non constante si le mouvement est circulaire non uniforme.
, constante si le mouvement est circulaire uniforme, non constante si le mouvement est circulaire non uniforme.
Dans le repère de Frenet, voici les expressions des vecteurs vitesse et accélération.
* ![]()
* ![]()
![]() est appelée l’accélération tangentielle
est appelée l’accélération tangentielle
![]() est appelée l’accélération normale.
est appelée l’accélération normale.
Si le mouvement est circulaire uniforme à la vitesse ![]() alors
alors
![]()
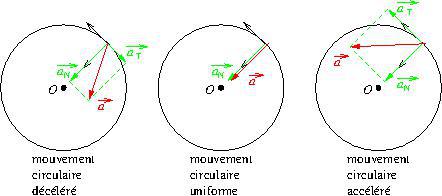
Elle est donc dirigée vers le centre ![]() et dite « centripète« . Ceci est conforme au fait que le vecteur accélération a la direction et le sens de l’inflexion du vecteur vitesse.
et dite « centripète« . Ceci est conforme au fait que le vecteur accélération a la direction et le sens de l’inflexion du vecteur vitesse.
Si le mouvement est circulaire et accéléré (![]() est une fonction croissante de
est une fonction croissante de ![]() ), alors l’accélération a deux coordonnées positives dans la base de Frenet.
), alors l’accélération a deux coordonnées positives dans la base de Frenet.
Si le mouvement est circulaire et décéléré (![]() est une fonction décroissante de
est une fonction décroissante de ![]() ), alors l’accélération a une coordonnée positive sur
), alors l’accélération a une coordonnée positive sur ![]() et négative sur
et négative sur ![]() dans la base de Frenet.
dans la base de Frenet.
Exemple
Un pilote de chasse a un mouvement circulaire de rayon ![]() , uniforme à la vitesse
, uniforme à la vitesse ![]()
Quelle est la norme de l’accélération qu’il subit ?
Correction :
![]()
(soit 7,4 « g », 7,4 fois l’accélération de la pesanteur).
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Retrouvez et entraînez-vous sur toutes les annales du bac de physique sur la Cinématique et toutes nos annales du bac de terminale afin d’être absolument certain de maîtriser au mieux le programme de terminale de physique-chimie. Vous pourrez ainsi être plus que serein au moment des résultats du bac. Voici aussi, quelques autres chapitres de physique-chimie à bien connaître pour exceller au bac :
- Cours mécanique des fluides en terminale
- Cours en ligne mouvements dans un champ uniforme terminale
- Cours sur les lois de Newton niveau bac
- Cours sur les acides et les bases en terminale
- Résumé de cours mesures physiques en chimie
- Exercices corrigés de cinématique en terminale
- Exercices corrigés de mécanique des fluides en terminale

