Cours en ligne Maths en Maths Spé

Chapitres Maths en MP, PSI, PC, TSI, PT

Cours en ligne Maths en Maths Spé

Chapitres Maths en MP, PSI, PC, TSI, PT

Courbes Paramétrées – PT

Name: Groupe Réussite: Cours particuliers, stages intensifs de révision
Brand: Groupe Réussite
SKU: Cours Particuliers
Rating: 4.9 (1049 reviews)

Résumé de cours Exercices Annales

Résumé de cours, méthodes et exercices – courbes paramétrées

Il y a une partie méthodes, partie avec 4 exemples de courbes paramétrées significatifs et un chapitre d’exercices sur les coniques.

Plan de cette partie méthode

1. Méthodes courbes paramétrées planes
2. Courbe donnée par une équation cartésienne.
3. Coniques

1. Courbes paramétrées planes

On suppose que $\mathcal{R} = \left (O , \overrightarrow{i} , \overrightarrow{j} \right )$ est un repère orthonormal de $\mathbb{R}^2$ (en général, c’est le repère canonique).

1.1. Domaine de définition et restriction du domaine d’étude

On cherche le domaine de définition $\mathcal{D}$ de la fonction $F$ d’une variable réelle $t$ à valeurs dans $\mathbb {R}^2$ , éventuellement on prolonge $F$ par continuité.

Lorsque $\mathcal{D}$ est une réunion d’intervalles, on parle de la courbe paramétrée $(\mathcal{D}, \, F)$ .
Dans la suite, on note :
$F : \mathcal{D} \to \mathbb{R}^2$ , $t \mapsto f(t)\, \overrightarrow{i} + g(t)\, \overrightarrow{j}$
et si $t \in \mathcal{D}$ , $\overrightarrow {OM(t)} = F(t)$ ;
$\Gamma$ la courbe représentative c’est à dire l’ensemble des points $M(t)$ lorsque $t$ décrit $\mathcal{D}$ .

Il y a lieu de restreindre le domaine d’étude dans les cas suivants :
$\bullet$ a) utilisation d’une période :
si $\forall \, t \in \mathcal{D}, t + P \in \mathcal{D}$ où $P > 0$ et $M(t + P) = M(t)$ : on étudie $F$ sur $[0 , \, P] \cap \mathcal{D}$ ou sur $[- P/2 ,\, P/2] \cap \mathcal{D}$ .

$\bullet$ b) utilisation de la parité : le domaine $\mathcal{D}$ étant symétrique par rapport à $0$ :
$\ast$ si $\forall\, t \in \mathcal{D}$ , $\, f(- t) = f(t) \textrm{ et } g(- t) = g(t)$ ,
$M(-t) = M(t)$ .
On étudie $F$ sur sur $\mathbb{R } ^+ \cap \mathcal{D}$
(la courbe est décrite deux fois).

$\ast$ si $\forall\, t \in \mathcal{D},\,$ $f(- t) = - f(t) \textrm{ et } g(- t) = - g(t)$ ,
$M(-t)$ et $M(t)$ sont symétriques par rapport à $O$ .
On étudie $F$ sur $\mathbb{R } ^+ \cap \mathcal{D}$ et on complète $\Gamma$ par symétrie par rapport à $O$ .

$\ast$ si $\forall\, t \in \mathcal{D},\,$ $f(- t) = - f(t) \textrm{ et } g(- t) = g(t)$ ,
$M(-t)$ et $M(t)$ sont symétriques par rapport à la droite $Oy$ .
On étudie $F$ sur $\mathbb{R } ^+ \cap \mathcal{D}$ et on complète $\Gamma$ par symétrie par rapport à $Oy$ .

$\ast$ si $\forall\, t \in \mathcal{D},\,$ $f(- t) = f(t) \textrm{ et } g(- t) = - g(t)$
$M(-t)$ et $M(t)$ sont symétriques par rapport à la droite $Ox$
On étudie $F$ sur $\mathbb{R } ^+ \cap \mathcal{D}$ et on complète $\Gamma$ par symétrie par rapport à $Ox$ .

$\bullet$ c) il y a d’autres restrictions possibles.
Par exemple, si l’on doit étudier $F$ sur $\mathcal{D} \cap [0 ,\, a]$ et si l’on peut trouver $\varepsilon$ et $\varepsilon '$ égaux à $\pm 1$ tels que $f(a - t) = \varepsilon f(t)$ et $g(a - t) = \varepsilon' g(t)$ , il suffit d’étudier $F$ sur $\mathcal{D}\cap [0,\, a/2]$ et de compléter la courbe $\Gamma$ par la symétrie convenable
(en effet $a - t$ décrit $[ a/2 , \,a]$ lorsque $t$ décrit $[0 ,\, a/2]$ ).
👍 Ne pas hésiter à faire un dessin pour placer $M(a - t)$ et $M(t)$

Pour accéder aux meilleurs cours particuliers à domicile ou en ligne, sélectionner le prof qu'il vous faut

Recherchez un prof particulier

1.2. Calcul de $f '$ , $g'$ , signe, sens de variation de $f$ et $g$ et début du tableau de variations

👍 Il est conseillé de placer les lignes donnant le sens de variation de $f$ et $g$ l’une sous l’autre.

1.3. Étude locale de l’arc paramétré

On suppose que dans le repère $\mathcal{R}$ : $\quad \quad \overrightarrow{OM(t)} = f(t)\, \overrightarrow{i}+ g(t) \, \overrightarrow{j}$ .

$\bullet$ 1. On étudie les points où une seule des dérivées $f ',\, g'$ s’annule.
$\ast$ Si $g'(t_0) = 0$ et $f '(t_0) \neq 0$ , la tangente en $M(t_0)$ est horizontale
$\ast$ Si $f'(t_0) = 0$ et $g '(t_0) \neq 0$ , la tangente en $M(t_0)$ est verticale.
$\ast$ Si le point $M(t_0)$ est régulier (soit $F'(t_0) \neq 0$ ), une équation de la tangente en $M(t_0)$ est $\quad \quad \left \vert \begin{matrix} x - f(t_0)& f'(t_0) \\ x - g(t_0)& g'(t_0) \end{matrix} \right \vert = 0$ .

$\bullet$ 2. On étudie les points stationnaires (ou singuliers).
$\ast$ Si l’on se limite à déterminer la tangente en $M(t_0)$ , on cherche le plus petit entier $p > 1$ tel que $\overrightarrow{V} = F^{(p)}(t_0)$ soit non nul.
Dans ce cas, la tangente en $M(t_0)$ à $\Gamma$ est la droite passant par $M(t_0)$ et de vecteur directeur $\overrightarrow{V}$ .

👍 Remarque : dans le cas d’un point stationnaire de paramètre $t_0\,$ , on peut aussi chercher la limite de la pente de la droite $(M(t_0)M(t))$ lorsque $t \to t_0$ , c’est à dire $\displaystyle \lim _{ t \to t_0} \frac {g(t) - g(t_0)} {f(t) - f(t_0)}$ .
$\ast$ Si la limite est un réel $m$ , la droite passant par $M(t_0)$ et de pente $m$ est tangente à $\Gamma$ en $M(t_0)$ .
$\ast$ Si la limite est $\infty$ , la tangente en $M(t_0)$ à $\Gamma$ est verticale.

$\ast$ Si l’on veut étudier complètement le point stationnaire, il faut déterminer les entiers (dits entiers caractéristiques) $p$ et $q$ tels que
$p$ est le plus petit entier supérieur ou égal à 1 tel que $\overrightarrow{V}= F^{(p)}(t_0)$ soit non nul et $q$ le plus petit entier strictement supérieur à $p$ tel que $\overrightarrow{W}= F^{(q)}(t_0)$ ne soit pas colinéaire à $\overrightarrow{V}$ .
Pour cela on a le choix entre :
$\ast$ le calcul des dérivées successives de $f$ et $g$ en $t_0$ .
$\ast$ l’utilisation des développements limités de $f$ et $g$ en $t_0$ à un ordre suffisant (3 convient dans la plupart des cas), pour cela on se ramène au voisinage de 0 en posant $u = t - t_0\,$ .
Grâce à la formule de Taylor-Young, on obtient les dérivées successives de $f$ et $g$ en $t_0\,$ .
En notant $\quad \overrightarrow{OM(t)}= F(t) = f(t)\, \overrightarrow{i}+ g(t) \, \overrightarrow{j}$ , on a donc obtenu les dérivées successives de $F$ en $t_0\,$ .

$\ast$ Dans le repère $\left ( M(t_0) , \overrightarrow{ V } , \, \overrightarrow{W} \right )$ , les coordonnées $(X , Y)$ de $M(t_0 + h)$
vérifient $\displaystyle X \underset {h \to 0} { \sim } \frac{ h ^p} {p!}$ et $\displaystyle Y \underset {h \to 0} { \sim } \frac{ h ^q} {q!}$ ,
$X$ est du signe de $h^p$ et $Y$ du signe de $h^q$ au voisinage de $0$ .

Démonstration

Pour tout $k$ tel que $p + 1 \leq k \leq q - 1$ (si de tels $k$ existent) , $F^{(k)}(t_0)$ est colinéaire à $\overrightarrow{V }$ , donc s’écrit
$F^{(k)}(t_0) = \mu_k \, \overrightarrow{V}$ avec $\mu_k \in \mathbb{R}$ .
Par la formule de Taylor-Young :
$\displaystyle F(t_0 + h) - F(t_0) \underset {h \to 0} { = }$ $\quad \quad \quad \displaystyle \frac{h^p} {p!} \, \overrightarrow {V} + \sum_{k = p + 1} ^{q - 1} \mu_k\, \frac {h ^k} {k!} \, \overrightarrow {V}$ $\quad \quad \quad \quad \quad \displaystyle + \frac{h^q} {q!} \,\left ( \overrightarrow {W} + \overrightarrow{\varepsilon(h)} \right)$ .
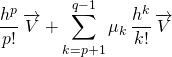
En notant 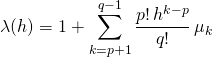$\displaystyle \lambda(h) = 1 + \sum _{k = p + 1} ^{q - 1} \frac {p ! \,h ^{k - p} } {q!} \, \mu_k\,$
on peut donc écrire au voisinage de $0$
$\displaystyle F(t_0 + h) - F(t_0) \underset {h \to 0} { = }$ $\quad \quad \quad \displaystyle \frac{h^p} {p!}\lambda(h) \, \overrightarrow {V}+ \frac{h^q} {q!} \,\left ( \overrightarrow {W} + \overrightarrow{\varepsilon(h)} \right)$
avec $\displaystyle \lim_{h \to 0} \lambda(h) = 1$ et $\displaystyle \lim_{h \to 0} \overrightarrow{\varepsilon(h)} = \overrightarrow{0}$ .

Dans le repère $\left ( M(t_0) , \overrightarrow{ V } , \, \overrightarrow{W} \right )$ , les coordonnées $(X\, , \, Y)$ de $M(t_0 + h)$ sont :
$\; \; \displaystyle X(t_0 + h) \underset {h \to 0} { = } \frac{ h ^p} {p!} \lambda(h) + \frac{ h ^q} {q!} \varepsilon_1(h)$
et $\displaystyle Y(t_0 + h) \underset {h \to 0} { =} \frac{ h ^q} {q!}(1 + \varepsilon_2(h))$
donc $\displaystyle X(t_0 + h) \underset {h \to 0} { \sim } \frac{ h ^p} {p!}$ et $\displaystyle Y(t_0 + h) \underset {h \to 0} { \sim} \frac{ h ^q} {q!}$

1.4. Branches infinies

def1 : On dit que $\Gamma$ a une branche infinie quand $t$ tend vers $a$ lorsque $\displaystyle \lim_{t\to a} OM(t) = \lim _ {t \to a} \Vert F(t) \Vert = + \infty$

def 2 : Si $\displaystyle \lim_{t\to a} OM(t)= +\infty$ et s’il existe une droite $\mathcal{D}$ telle que
$\quad \quad \quad \displaystyle \lim_{t \to a} d(M(t) , \mathcal{D}) = 0$ ,
on dit que la droite $\mathcal{D}$ est asymptote à l’arc $\Gamma$ .

👍 En pratique, on a une branche infinie quand l’une au moins des fonctions $t\mapsto \vert f(t) \vert$ , $t \mapsto \vert g(t) \vert$ tend vers $+\infty$ lorsque $t$ tend vers $a$ .

Cas usuels de branche infinie :
$\bullet$ Cas 1 :
$\displaystyle \lim_{t \to a} f(t) = x_0$ et $\displaystyle \lim _{t \to a} \vert g(t) \vert = + \infty$ ,
la droite d’équation $x = x_0$ est asymptote à $\Gamma$ .

$\bullet$ Cas 2 :
$\displaystyle \lim_{t \to a} g(t) = y_0$ et $\displaystyle \lim _{t \to a} \vert f(t) \vert = + \infty$ ,
la droite d’équation $y = y_0$ est asymptote à $\Gamma$ .

$\bullet$ Cas 3 :
$\displaystyle \lim_{t \to a} \vert f(t)\vert = +\infty$ et $\displaystyle \lim _{t \to a} \vert g(t) \vert = + \infty$ ,
on étudie la limite en $a$ de $t \mapsto \displaystyle \frac {g(t)} {f(t)}$ .

$\ast$ sous-cas 1 : $\displaystyle \lim_{t \to a} \frac {g(t)} {f(t)} = 0$ , $\Gamma$ admet une branche parabolique de direction $Ox$ .
$\ast$ sous-cas 2 : $\displaystyle \lim_{t \to a} \frac {g(t)} {f(t)} = \infty$ , $\Gamma$ admet une branche parabolique de direction $Oy$ .
$\ast$ sous-cas 3 : $\displaystyle \lim_{t \to a} \frac {g(t)} {f(t)} = \alpha \neq 0$ et $\displaystyle \lim_{t \to a} g(t) - \alpha f(t) = \infty$ , $\Gamma$ admet une branche parabolique de direction $y = \alpha x$ .
$\ast$ sous-cas 4 : $\displaystyle \lim_{t \to a} \frac {g(t)} {f(t)} = \alpha \neq 0$ et $\displaystyle \lim_{t \to a} g(t) - \alpha f(t) = \beta$ ,
la droite $\Delta$ d’équation $y = \alpha x + \beta$ est asymptote à $\Gamma$ . Le signe de $g(t) - \alpha f(t) - \beta$ au voisinage de $a$ donne la position de $\Gamma$ par rapport à $\Delta$
… La courbe est au dessus de $\Delta$ lorsque $g(t) - \alpha f(t) - \beta > 0$
… La courbe est en dessous de $\Delta$ lorsque $g(t) - \alpha f(t) - \beta < 0$ .

1.5. Tracé :

$\bullet$ Commencer par placer les asymptotes, les points particuliers et les tangentes.
$\ast$ Se positionner (au dessus / en dessous, à droite / à gauche) pour les asymptotes horizontales suivant les valeurs de $t$ .
$\ast$ Se positionner (à droite / à gauche, en haut / en bas) pour les asymptotes verticales suivant les valeurs de $t$ .
$\ast$ Se positionner (au dessus / en dessous), en faisant en plus attention au signe de $x$ et $y$ pour les asymptotes obliques.

$\bullet$ Si la calculatrice est utilisable, on programme les fonctions $t \mapsto f(t)$ et $t \mapsto g(t)$ pour calculer les coordonnées d’autres points.

1.6. Points doubles

Si l’on s’aperçoit après tracé qu’il y a des points doubles, il faut les déterminer.

$\bullet$ Cas 1 : $f$ et $g$ sont des fractions rationnelles.
On cherche $t \neq u$ tels que $f(t) = f(u)$ et $g(t) = g(u)$ .
$\ast$ Faire le produit en croix. Simplifier par $t - u$ et exprimer les équations obtenues en fonction de $S = t + u$ et $P = t u$ .
$\ast$ Déterminer $S$ et $P$ (il est inutile de chercher $t$ et $u$ sauf si l’énoncé le demande).
$\ast$ Calculer les coordonnées du point double en utilisant le fait que $t$ vérifie $t^2 - S t + P = 0$ (calcul de $t$ inutile, remplacer $t^2$ par $S t - P$ ).

$\bullet$ Cas 2 : $f$ et $g$ sont des lignes trigonométriques.
$\ast$ On cherche d’abord à encadrer les nombres $t$ et $u$ .
$\ast$ On résout les équations trigonométriques ce qui fait en général intervenir une ou plusieurs constantes $k$ de $\mathbb{Z}$ . On utilise l’encadrement de $t$ et $u$ pour obtenir les valeurs nécessaires de $k$ (une ou plusieurs valeurs selon les cas) et on termine la résolution.

Il faudra éventuellement corriger le tracé obtenu précédemment.
Un autre exemple est présenté avec la deuxième courbe de la tâche suivante.

Exemple

Soit la courbe paramétrée définie par $\quad x(t) = \displaystyle \frac {2 t - 1} {t ^2 - 1}$ et $y(t) = \displaystyle \frac {t^2} {t - 1}$ .
Déterminer son point double.

Corrigés :

On cherche $t \neq u$ tel que $x(t) = x(u)$ et $y(t) = y(u)$ .

$\bullet$ Première équation
$x(t) = x(u)$ $\Leftrightarrow (u ^2 - 1) (2 t - 1) = (t ^2 - 1)(2 u - 1)$
$\Leftrightarrow 2 t u ^2 - 2 t - u ^2 + 1 =$ $\quad \quad \quad \quad 2 u t ^2 - 2 u - t^2 + t - 1$
$\Leftrightarrow 2 t u (u - t) -( u ^2 - t^2) + 2 (u - t) = 0$
en simplifiant par $u - t \neq 0$
$\Leftrightarrow 2\, t \, u -( u + t) + 2 = 0$
En notant $S = t + u$ et $P = t \, u$ , on obtient une première condition $2\, P - S + 2 = 0$

$\bullet$ Deuxième équation
$y(t) = y(u)$ $\Leftrightarrow (u - 1) t ^2 = (t - 1) u ^2$
$\Leftrightarrow t ^2 u - t u ^2 + u ^2 - t ^2 = 0$
$\Leftrightarrow t u (t - u) - ( t ^2 - u^2) = 0$
en simplifiant par $t - u \neq 0$
$\Leftrightarrow t\, u - ( u + t)= 0$
On obtient une deuxième condition : $P - S = 0$

$\bullet$ Les relations $2 \, P - S + 2 = 0$ et $P - S = 0$ donnent $S = P = - 2 0$
$t$ vérifie $t ^2 + 2\, t - 2 = 0$ soit $t^2 = 2 - 2 \, t$
$x(t) = \displaystyle \frac {2 t - 1} {t ^2 - 1} = \frac {2 t - 1} {1 - 2 t} = - 1$
et $y(t) = \displaystyle \frac {t ^2 } {t - 1} = \frac {2 - 2 t} {t - 1 } = - 2$
Le point double a pour coordonnées $( - 1 , - 2)$ .

2. Courbe donnée par une équation cartésienne

Si $f$ est de classe $C^1$ sur l’ouvert $U$ de $\mathbb{R}^2$ , on note $\Gamma$ la courbe d’équation cartésienne $f(x , y) = 0$ .
Soit $M(a , b) \in \Gamma$ $(f(a , b) = 0)$ tel que $\nabla f(a ,\, b)\neq 0$ . Le point $M(a ,\, b)$ est dit régulier.
La tangente en $M(a ,\, b)$ à $\Gamma$ est la droite passant par $M$ et orthogonale à $\nabla f(a ,\, b)$ .
Elle a pour équation :
$\displaystyle \frac {\partial f} {\partial x} (a , \, b) \, (x - a)+ \frac {\partial f} {\partial y} (a , \, b) \, (y - b)$ $= 0$

Exercice
Reconnaître la courbe d’équation $\quad \quad x ^2 + y^2 - 2\, x - 4 \, y + 1 = 0$ .
Déterminer de deux façons différentes une équation de la tangente à $\Gamma$ au point de cordonnées $( a\, ,\, b)$ .

Corrigé

$\bullet$ On écrit l’équation sous la forme :

$\quad \quad \quad (x - 1) ^2 + (y - 2) ^2 = 4$ .

$\Gamma$ est le cercle de centre

$\Omega (1\, ,\, 2)$ et de rayon

$R = 2$ .

$\bullet$ Première méthode :

$\Gamma$ est la courbe d’équation

$\varphi(x , y) = 0$ avec

$\varphi : (x , y) \mapsto x^2 + y ^2 - 2 x - 4 y + 1$ , qui est une fonction de classe

$C^1$ sur

$\mathbb{R}^2$ .

$\nabla \varphi (a\, ,\, b) = (2 a - 2 \, , \, 2 b - 4)$ est non nul car

$\nabla \varphi (a\, , \, b) = 0$ ssi

$a = 1, \, b = 2$ .
Comme

$\varphi(1 , 2) \neq 0$ , tout point de

$\Gamma$ est régulier.

La tangente à $\Gamma$ en $A(a, b)$ est la droite passant par $A$ et orthogonale à $\nabla \varphi (a , b)$
Elle a pour équation :
$(a - 1) ( x - a) + (b - 2) ( y - b) = 0$
ssi $(a - 1) x + (b - 2) y = a^2 - a + b^2 - 2 b$
ssi $(a - 1) x + (b - 2) y = a + 2 b - 1$ .

$\bullet$ Deuxième méthode
On peut paramétrer le cercle par $\quad \quad x = 1 + 2\, \cos(t)$ , $y = 2 + 2 \, \sin(t)$ .

Si $A(a\, ,\, b)$ est le point de paramètre $t$ , la tangente en $A$ est dirigée par le vecteur $(x'(t)\, ,\, y'(t)) = (- 2 \sin(t) \, , \, 2 \cos(t))$ et pour équation
$\left \vert \begin{matrix} x - 1 - 2 \cos(t) & - \sin(t)\\ y - 2 - 2 \sin(t) & \cos(t) \end{matrix} \right \vert = 0$
soit $\cos(t) \, x +\sin(t)\, y - \cos(t) - 2 \sin(t)$ $\quad \quad \quad - 2\sin^2(t) - 2 \cos^2(t)= 0$
ssi $\cos(t)\, x +\sin(t)\, y = \cos(t) + 2 \sin(t) + 2$
puis en multipliant l’équation par 2 :
ssi $(a - 1) x + (b - 2) y = a - 1 + 2 b - 4 + 4$

car $a = 1 + 2 \cos(t)$ et $b = 2 + 2 \sin(t)$ .

Pour accéder aux meilleurs cours particuliers à domicile ou en ligne, sélectionner le prof qu'il vous faut

Recherchez un prof particulier

Pour avoir accès à de nombreux autres chapitres de maths en Maths Spé, rendez-vous sur les cours en ligne de Maths en PSI, les cours en ligne de Maths en MP mais aussi les cours en ligne de PC en Maths, sans oublier les cours en ligne de PT en Maths.

3. Equations réduites des coniques

def : On appelle conique toute courbe $\mathcal{C}$ d’équation :
$a x^2 + 2 b x y + c y^2 + 2 d x + 2 e y + f = 0$ où $(a , b , c) \neq (0 , 0 , 0)$ .

3.1. Ellipse

$\mathcal{E}$ d’équation si $0 < b < a$ , $\quad \quad \quad \displaystyle \frac {x^2} {a^2} + \frac {y ^2} {b ^2} = 1$

Remarque : dans le cas où $0 < a < b$ , il faut échanger les axes $Ox$ et $Oy$ .

$\bullet$ La courbe $\mathcal{E}$ admet
$\quad \ast$ $O$ pour centre de symétrie.
$\quad \ast$ $x'x$ et $y'y$ pour axes de symétrie.
$\quad \ast$ $A(a\, , \, 0)$ et $A'(-a\, , \, 0)$ sont les sommets du grand axe
Le segment $[0 , \, A]$ est appelé demi-grand axe de $\mathcal{E}$
$\quad \ast$ $B(0 \, ,\, b)$ et $B'(0 \, ,\, -b)$ sont les sommets du petit axe.

$\bullet$ Une représentation paramétrique de $\mathcal{E}$ est définie par
$\quad \quad [0 , 2 \pi] \to \mathbb{R}^2$ $\quad \quad t \mapsto (a \, \cos(t) \, , \, b \, \sin(t))$ .

$\bullet$ La tangente en $M_0 (x_0 \, , \, y_0) \in \mathcal{E}$ a pour équation $\displaystyle \frac {x_0 \, x} {a^2} + \frac {y_0 \, y} {b ^2} = 1$ .

3.2. Hyperbole

$\mathcal{H}$ d’équation si $0 < b$ et $0 < a$ , $\quad \quad \displaystyle \frac {x^2} {a^2} - \frac {y ^2} {b ^2} = 1$

Remarque : dans le cas d’une équation de la forme $\displaystyle \frac {y^2} {b^2} - \frac {x ^2} {a ^2} = 1$ , il faut échanger les axes $Ox$ et $Oy$ .

$\bullet$ La courbe $\mathcal{H}$ admet
$\quad \ast$ $O$ pour centre de symétrie.
$\quad \ast$ $x'x$ et $y'y$ pour axes de symétrie.
$\quad \ast$ $A(a\, , \, 0)$ et $A'(-a\, ,\, 0)$ sont les sommets du grand axe
$\quad \ast$ Les droites d’équation $y = \displaystyle \frac {a} {b} \, x$ et $y = \displaystyle - \frac {a} {b}\, x$ sont asymptotes à l’hyperbole.
L’hyperbole est dite équilatère lorsque $a = b$ , dans ce cas les asymptotes sont orthogonales.
👍 : on retrouve les équations des asymptotes en résolvant
$\quad \quad \quad \quad \displaystyle \frac {x^2} {a^2} - \frac {y ^2} {b ^2} = 0$ .

$\bullet$ Une représentation paramétrique de $\mathcal{H}$ est définie par
$\mathbb{R}^* \to \mathbb{R}^2$
$\displaystyle t \mapsto \left (\frac a 2 \left ( t + \frac 1 t \right ) \, , \, \frac b 2 \, \left ( t - \frac 1 t \right ) \right)$ .

👍 On retrouve cette représentation paramétrique en écrivant l’équation de $\mathcal{H}$ sous la forme
$\quad \quad \displaystyle \left ( \frac {y} {b} - \frac {x} {a} \right ) \,\left ( \frac {y} {b} + \frac {x} {a} \right ) = 1$
et en posant $\displaystyle t = \frac {y} {b} + \frac {x} {a}$ .

$\bullet$ On obtient une représentation paramétrique de la moitié de l’hyperbole située dans le demi plan $x > 0$ (resp. $x < 0$ ) par :
$\quad \quad \mathbb{R} \to \mathbb{R}^2$ , $t \mapsto (a \, \textrm{ch} (t) \, , \, b \, \textrm{sh}(t))$
(resp. $t \mapsto ( - a \, \textrm{ch} (t) \, , \, b \, \textrm{sh}(t))$ ).

3.3. Parabole

$\mathcal{P}$ d’équation si $p >0$ , $\displaystyle y ^2 = 2 \, p \, x$
$p$ est appelé paramètre de la parabole.

$\bullet$ La courbe $\mathcal{P}$ admet
$\quad \ast$ $x'x$ pour axe de symétrie.
$\quad \ast$ $O$ est le sommet de $\mathcal{P}$ et $y'y$ est la tangente en $O$ à $\mathcal{P}$ .

$\bullet$ Une représentation paramétrique de $\mathcal{P}$ est définie par :
$\quad \quad\mathbb{R } \to \mathbb{R}^2 \, , \, \displaystyle t \mapsto \left ( \frac {t^2} {2 p} \, ,\, t \right)$
ou aussi $t \mapsto \left (2 \, p \, t ^2 \, ,\,2 \, p \, t \right)$ .

$\bullet$ La tangente en $M_0 (x_0 \, , \, y_0) \in \mathcal{P}$ a pour équation $y _0 \, y = p (x + x_0)$ .

4. Obtenir une équation réduite

Conique $\mathcal{C}$ d’équation :
$a x^2 + 2 b x y + c y^2 + 2 d x + 2 e y + f = 0$ où $(a , b , c) \neq (0 , 0 , 0)$ .

L’équation d’une conique est la somme
$\ast$ d’une forme quadratique $\quad \quad \Phi(x , y) = a\, x^2 + 2 \,b \, x\, y + c\, y^2$ ,
$\ast$ d’une partie linéaire $\quad \quad \quad L(x , y) = 2 \, d\, x + 2\, e\, y$
$\ast$ et d’une constante $f$ .

4.1. cas où $b = 0$

$\bullet$ M1 Si $a = c$ et $b = 0$ , $\mathcal{C}$ est selon les valeurs des coefficients
$\quad \ast$ $\varnothing$
$\quad \ast$ un point
$\quad \ast$ un cercle.

Démonstration

$\mathcal{C}$ a pour équation :

$a(x^2 + y^2 ) + 2 \, d\, x + 2\, e \, y + f = 0$
ssi $x^2 + y^2 + 2\, d'\, x + 2\, e'\, y + f ' = 0$
ssi $(x + d')^2 + (y + e')^2 = {d'} ^2 + {e'} ^2 - f '$ .
avec $a\, d' = d , \, a\, e' = e, \, a\, f' = f$

donc ${d'} ^2 + {e'} ^2 - f ' = \displaystyle \frac {1} {a^2} (d^2 + e ^2 - a f )$ $\ast$ Si $d^2 + e ^2 - a f \geq 0$ , $\mathcal{C}$ est un cercle de centre $(- d/a ,\, - e/a)$ éventuellement réduit à un point
$\ast$ Si $d^2 + e ^2 - a f < 0$ , $\mathcal{C} = \varnothing$ .

$\bullet$ M2. Si $a \, c \neq 0$ et $b = 0$ , écrire l’équation $\quad a\, x^2 + c \, y^2 + 2 \, d \, x + 2\, e \, y + f = 0$ sous la forme $\displaystyle a \left ( x + \frac d a \right ) ^2 + c \left ( y + \frac e c \right ) ^2 + f ' = 0$ avec $\displaystyle f ' = f - \frac {d^2} {a} - \frac {e^2} c$ . Si $f' \neq 0$ , on obtient $\ast$ une ellipse si $a \, c > 0$ et $f' \, a < 0$ $\ast$ une hyperbole si $a \, c < 0$ . Si $f' = 0$ , on obtient selon le cas $\varnothing$ , un point ou deux droites concourantes.

$\bullet$ M3. Si $a = b = 0$ , écrire l’équation sous la forme $\; \; \displaystyle c \left ( y + \frac e c \right ) ^2 + 2\, d\, x + f - \frac {e^2} c = 0$ . $\ast$ si $d \neq 0$ , on obtient une parabole. $\ast$ si $d = 0$ , on obtient $\varnothing$ , une droite ou deux droites distinctes.

$\bullet$ M3bis Si $c = b = 0$ , raisonner de même en échangeant $x$ et $y$ .

4.2. Cas général $b \neq 0$

Notations : Soit $A = \begin{pmatrix} a&b\\b&c \end{pmatrix}$ et $L = \begin{pmatrix} d & e \end{pmatrix}$ et $X = \begin{pmatrix} x \\y \end{pmatrix}$ , l’équation de $\mathcal{C}$ s’écrit : $\quad \quad X^{\textrm{T}} \, A \, X + 2\, L\, X + f = 0$

⚠️ à bien écrire comme terme hors diagonale de $A$ , la moitié du coefficient de $x\, y$ .

4.2.2. Centre de symétrie si $A$ est inversible. Soit $\mathcal{C}$ la courbe du second degré d’équation $F(x , y) = 0$ avec $F(x , y) = X^{\textrm{T}} \, A \, X + 2\, L\, X + f = 0$ .

Si $A$ est inversible, $\mathcal{C}$ admet un unique centre de symétrie $O'(x_0 \, , \, y_0)$ où $(x_0 \, , \, y_0)$ est le seul point critique de $F$ (c’est à dire vérifie $\nabla F(x_0 \, , \, y_0) = 0$ ou encore $A \, X_0 + L ^{\textrm{T}} = 0$ ).

Dans le repère $\mathcal{R'} \left ( O' \, , \, \overrightarrow{i} \, , \, \overrightarrow{j}\right )$ , $\mathcal{C}$ a pour équation $\quad \quad {X'}^{\textrm{T}} \, A \, X' + F(x_0 \, , \, y_0) = 0$ .

4.2.3. Utilisation de la réduction

La matrice symétrique réelle $A$ admet deux valeurs propres réelles $\lambda , \, \mu$ et soit $\mathcal{B}' = \left(\overrightarrow{u} \, , \,\overrightarrow{v}\right )$ une base orthonormale de vecteurs propres. Dans le repère $\mathcal{R}' \left ( O\, , \overrightarrow{u}\, , \,\overrightarrow{v} \right )$ , $\mathcal{C}$ a pour équation $\lambda \, {x'} ^2 + \mu\, {y'} ^2 + 2 d'\, x' + 2 e'\, y' + f = 0$ avec $L' = \begin{pmatrix} d' & e' \end{pmatrix} = L \, P$ où $P$ est la matrice de passage de la base canonique à la base $\mathcal{B}'$ .

👍 Si l’on a déterminé $\overrightarrow{u}$ vecteur propre unitaire associé à la valeur propre $\lambda$ de coordonnées $(a , b)$ , le vecteur $\overrightarrow{v}$ de coordonnées $(- b \, , \, a)$ , est un vecteur propre unitaire associé à l’autre valeur propre de $A$ .

$\mathcal{C}$ a pour équation $\lambda \, {x'} ^2 + \mu\, {y'} ^2 + 2 d'\, x' + 2 e'\, y' + f = 0$

Si $\textrm{det}(A) = 0$ , on choisit $\lambda = 0$ . Alors $µ \neq 0$ car $A \neq 0$ .
Dans le repère $\mathcal{R}'$ , l’équation est $\mu\, {y'} ^2 + 2 d'\, x' + 2 e'\, y' + f = 0$
ssi $\displaystyle \mu \left ( y ' + \frac {e'} {\mu} \right ) ^2 + 2 d'\, x' + f' - \frac {e'^2} {\mu} = 0$ .

$\bullet$ si $d' = 0$ , on obtient une équation de la forme $\displaystyle \mu \left ( y ' + \frac {e'} {\mu} \right ) ^2 + f''= 0$ donc deux droites, un point ou $\varnothing$ .
$\bullet$ si $d' \not= 0$ , on obtient une équation de la forme ${y''}^2 = 2 p \, x''$ par changement d’origine.

Pour accéder aux meilleurs cours particuliers à domicile ou en ligne, sélectionner le prof qu'il vous faut

Recherchez un prof particulier

Exercices sur les Courbes Paramétrées en maths spé

4 courbes sont étudiées dans ce chapitre :
1. L’astroïde $F : t \mapsto (a \cos^3(t), \, a \sin^3(t))$ où $a > 0$ , quelques propriétés géométriques et la longueur (en PSI).
2. $F : t \mapsto (\sin(2 t) , \sin(3 t))$ .(avec un point double)
3. $x(t) = \displaystyle \frac {2 t + 1} {t( t + 1)}$ et $y(t) = \displaystyle \frac {2 t - 1} {t(t - 1)}$ (avec un point double)
4. $x(t) =\displaystyle \frac 1 {t ^2} + 2 t$ ; $y(t) = \displaystyle t + \frac 1 t$ (un point stationnaire et une recherche de parabole asymptote)

1. Exemple 1 : astroïde

$F : t \mapsto (a \cos^3(t), \, a \sin^3(t))$ où $a > 0$ .
Question 1
Déterminer le domaine d’étude de la courbe paramétrée

On étudie sur $[0 , a ]$ avec $a =$

Question 2
Etudier les variations de $x$ et $y$ et donner le tableau de variation*

Question 3
Tracer le graphe

Question 4
Soit $M$ un point de l’astroïde n’appartenant pas aux axes.
La tangente en $M$ à $\Gamma$ coupe $Ox$ en $P$ et $Oy$ en $Q$ .
Calculer la longueur du segment $PQ$ . Est-elle contante ?

Question 5
Soit $\mathcal{C}$ un cercle de centre $O$ et de rayon $a$ .
Si $C$ est un point de $\mathcal{C}$ différent des axes, on note $A$ sa projection sur $Ox$ et $B$ sa projection sur $Oy$ . Soit $M$ la projection orthogonale de $C$ sur $(AB)$ . Calculer les coordonnées de $M$ .
Lorsque $C$ est un point des axes, on note $M = C$ .

Question 6
Calculer la longueur de l’astroide.

2. Exemple 2

$F : t \mapsto (\sin(2 t) , \, \sin(3 t))$ .

Question 1
Déterminer le domaine de définition et restreindre le domaine d’étude.

Question 2
Calculer les dérivées, préciser les tangentes aux points remarquables.
Donner le tableau de variation.

Question 3
Tracer la courbe.

Question 4
Déterminer les points doubles.

3. Exemple 3

Soit la courbe paramétrée définie par $x(t) = \displaystyle \frac {2 t + 1} {t( t + 1)}$ et $y(t) = \displaystyle \frac {2 t - 1} {t(t - 1)}$ .
Question 1
Déterminer le domaine de définition.

Question 2
Etudier les dérivées, les tangentes aux points particulier s’il y a lieu et donner le tableau de variation

Question 3
Etudier les banches infinies de la courbe

Question 4
Etudier le point limite.

Question 6
Tracer le graphe.

Question 7
Etudier le point double

Pour accéder aux meilleurs cours particuliers à domicile ou en ligne, sélectionner le prof qu'il vous faut

Recherchez un prof particulier

4. Exemple 4

Soit la courbe paramétrée définie par :
$\quad x(t) =\displaystyle \frac 1 {t ^2} + 2 t$ ; $y(t) = \displaystyle t + \frac 1 t$ .
Question 1.
Déterminer le domaine de définition, calculer les dérivées, préciser les tangentes aux points réguliers particuliers et donner le tableau de variation.

Question 2
Etudier le point stationnaire

Question 3
Etudier les branches infinies de $\Gamma$ .

Question 4
Montrer qu’il existe une parabole asymptote

Question 5
Représenter $\Gamma$ , ses asymptotes et la parabole asymptote.

Exercices sur les Coniques en maths spé

Plan

1. Réduction d’une conique : exemple 1
2. Réduction d’une conique : exemple 2
3. Réduction d’une conique : exemple 3
4. Réduction d’une conique : exemple 4
5. Parabole et géométrie
6. Construction de l’ellipse point par point.

1. Exemple 1 de réduction d’une conique

Question 1

Caractériser la conique $\mathcal{C}$ d’équation $\quad \quad 4 x^2 + y ^2 + 4\, x - 2\, y - 6 = 0$
et la représenter.

Question 2
Déterminer les points de $\mathcal{C}$ où la tangente est parallèle à la droite $\Delta$ d’équation $2 \, x + y = 0$ .

2. Exemple 2

Caractéristiques de la conique $\quad \mathcal{C} : x^2 + x \,y + y ^2 + x - y = 0$ et représentation.

3. Exemple 3

Caractéristiques de la conique $\quad \mathcal{C} : x \, y + 3 \, x + 5 \, y - 4 = 0$
et représentation.

4. Exemple 4

Caractéristiques de la conique $\mathcal{C}$ $16 \, x^2 + 9 \, y ^2 + 24 \, x \, y + 10 \, x$ $\quad\quad \quad \quad \quad \quad \quad + \, 70 \, y + 75 = 0$
et représentation.

5. Parabole et géométrie

Soit $a > 0$ , $F(a , 0)$ et $\mathcal{D}$ la droite d’équation $x = - a$ .
Question 1
L’ensemble $\mathcal{P}$ des points équidistants de $F$ et $\mathcal{D}$ est une parabole.

Question 2
Soit $M(t)$ le point de $\mathcal{P}$ d’ordonnée égale à $2\, a \, t$ et $\mathcal{D}_t$ la tangente en $M(t)$ à $\mathcal{P}$ .
Soit $H$ la projection orthogonale de $M(t)$ sur la droite $\mathcal{D}$ .
La tangente en $M(t)$ est la médiatrice du segment $[F , H]$ et la bissectrice de l’angle $F M(t) H$ .

Question 3
On suppose que $t \neq 0$ . On note $T$ le point d’intersection de la tangente en $M(t)$ et de la droite $\mathcal{D}$ .
Le triangle $M(t)\, F\, T$ est rectangle en $F$ .

6. Construction de l’ellipse

Soit $\mathcal{E}$ l’ellipse d’équation $\displaystyle \frac {x^2} {a^2} + \frac {y ^2} {b ^2} = 1$ et $M$ le point de coordonnées $(a \cos t , \, b \, \sin t)$ où $\cos t \, \sin t \neq 0$ .

Trouver le point d’intersection de la tangente en $M$ à l’ellipse et de la tangente en $M_1(a \cos t\, ,\, a \sin t)$ au cercle $\Gamma$ de centre $O$ et de rayon $a$ .
En déduire une construction de $M$ et de la tangente en $M$ à $\mathcal{E}$ .

Annales sur les courbes paramétrées en maths spé

Rendez-vous sur les annales de maths spé en mathématiques pour vous tester en conditions réelles.

Si certains exercices des annales vous paraissent trop compliqués, jetez un œil aux chapitres de maths qui vous posent problème grâce à l’ensemble des cours en ligne de maths en maths spé. Quelques exemples de cours à étudier :

Courbes Paramétrées – PT

Résumé de cours, méthodes et exercices – courbes paramétrées

Plan de cette partie méthode

1. Courbes paramétrées planes

1.1. Domaine de définition et restriction du domaine d’étude

Pour accéder aux meilleurs cours particuliers à domicile ou en ligne, sélectionner le prof qu'il vous faut

1.3. Étude locale de l’arc paramétré

Démonstration

1.4. Branches infinies

1.5. Tracé :

1.6. Points doubles

Exemple

Corrigés :

2. Courbe donnée par une équation cartésienne

Pour accéder aux meilleurs cours particuliers à domicile ou en ligne, sélectionner le prof qu'il vous faut

3. Equations réduites des coniques

3.1. Ellipse

3.2. Hyperbole

3.3. Parabole

4. Obtenir une équation réduite

Pour accéder aux meilleurs cours particuliers à domicile ou en ligne, sélectionner le prof qu'il vous faut

Exercices sur les Courbes Paramétrées en maths spé

1. Exemple 1 : astroïde

2. Exemple 2

3. Exemple 3

Pour accéder aux meilleurs cours particuliers à domicile ou en ligne, sélectionner le prof qu'il vous faut

4. Exemple 4

Exercices sur les Coniques en maths spé

1. Exemple 1 de réduction d’une conique

2. Exemple 2

3. Exemple 3

4. Exemple 4

5. Parabole et géométrie

6. Construction de l’ellipse

Annales sur les courbes paramétrées en maths spé

Contact

Qui sommes-nous ?

Nous rejoindre

Copyright @ GROUPE REUSSITE - Mentions légales