Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Équations différentielles linéaires en MP, PC, PSI et PT
Résumé de cours Exercices Annales
Résumé de cours et méthodes – Équations différentielles linéaires
Plan
1. Résolution d’une équation différentielle linéaire scalaire d’ordre 1 (paragraphe de révision du programme de première année).
2. Équation différentielle linéaire vectorielle du premier ordre
3. Équation ![]() où
où ![]()
4. Résolution de ![]() où
où ![]() et
et ![]() .5. Transformer une équation différentielle scalaire d’ordre
.5. Transformer une équation différentielle scalaire d’ordre ![]() en une équation différentielle vectorielle d’ordre 1
en une équation différentielle vectorielle d’ordre 1
6. Résolution d’équations différentielles linéaires scalaires d’ordre 2
7. Équation différentielle linéaire du second ordre à coefficients constants (Programme de maths sup)
8. Quelques autres méthodes de résolutions d’équations différentielles linéaires du second ordre.
8.1. Par changement de fonction inconnue
8.2. Méthode de Lagrange
8.3. Par utilisation d’une série entière
8.4. Par changement de variable
8.5. Cas des équations d’Euler
8.6. En cherchant une solution particulière sous la forme d’une fonction polynôme
8.7. Méthode de la variation des constantes (avec indications de l’énoncé) .
1. Résolution d’une équation linéaire scalaire d’ordre 1
1.1. Résolution de l’équation différentielle
![]()
où ![]() et
et ![]() sont des fonctions continues sur un intervalle
sont des fonctions continues sur un intervalle ![]() à valeurs dans
à valeurs dans ![]() .
.
Première étape.
On se place sur un intervalle ![]() sur lequel
sur lequel ![]() sont continues et l’application
sont continues et l’application ![]() ne s’annule pas et on utilise l’équation normalisée (après division par
ne s’annule pas et on utilise l’équation normalisée (après division par ![]() )
) ![]()
et l’équation sans second membre associée ![]() .
.
Si ![]() et si la fonction
et si la fonction ![]() s’annule sur
s’annule sur ![]() en un unique point
en un unique point ![]() , on sera amené à poser
, on sera amené à poser ![]() et
et ![]() et à résoudre l’équation
et à résoudre l’équation ![]() sur
sur ![]() et sur
et sur ![]() .
.
On gagne du temps s’il est possible de résoudre ![]() sur
sur ![]() où
où ![]() , sans être obligé de faire deux études différentes (l’une sur
, sans être obligé de faire deux études différentes (l’une sur ![]() , l’autre sur
, l’autre sur ![]() ).
).
À la fin, il faudra donner l’ensemble des solutions sur ![]() puis l’ensemble des solutions sur
puis l’ensemble des solutions sur ![]() .
.
1.1.1. Résolution de l’équation sans second membre ![]() .
.
On détermine une primitive ![]() de
de ![]() sur l’intervalle
sur l’intervalle ![]() .
.
La solution générale de ![]() est donnée par :
est donnée par : ![]() où
où ![]() .
.
Cas particulier :
Si ![]() , l’ensemble des solutions de
, l’ensemble des solutions de ![]() sur
sur ![]() est l’ensemble des fonctions
est l’ensemble des fonctions ![]() ,
, ![]() où
où ![]() .
.
Dans le cas où ![]() , une solution de
, une solution de ![]() est soit nulle sur
est soit nulle sur ![]() , soit ne s’annule pas sur
, soit ne s’annule pas sur ![]() et garde alors un signe constant sur
et garde alors un signe constant sur ![]() .
.
Donc lorsque la solution générale de ![]() s’écrit sous la forme
s’écrit sous la forme ![]() où
où ![]() ,
,
comme la fonction ![]() ne s’annule pas sur
ne s’annule pas sur ![]() , elle a un signe constant donc la solution générale de
, elle a un signe constant donc la solution générale de ![]() peut s’écrire
peut s’écrire ![]() ou
ou ![]() , donc en résumé sous la forme
, donc en résumé sous la forme ![]() où
où ![]()
On peut donc « supprimer » la valeur absolue.
1.1.2. Détermination d’une solution particulière de ![]() .
.
a) Elle peut être évidente.
b) Sinon, on utilise la méthode de variation de la constante.
Ayant trouvé comme solution de ![]() ,
, ![]() , on note
, on note ![]() .
.
On écrit que ![]() est solution de
est solution de ![]() sur
sur ![]() Le terme en
Le terme en ![]() doit disparaître et on obtient :
doit disparaître et on obtient :
![]() est solution sur
est solution sur ![]() de
de ![]()
![]()
![]() .
.
![]() En général, on peut déterminer une primitive de
En général, on peut déterminer une primitive de ![]() .
.
![]() Si l’on ne sait pas déterminer une primitive de cette fonction à l’aide des fonctions usuelles, on introduit
Si l’on ne sait pas déterminer une primitive de cette fonction à l’aide des fonctions usuelles, on introduit ![]() et on dit qu’il existe
et on dit qu’il existe ![]()
![]() .
.
Dans ce cas, l’ensemble des solutions sur ![]() est l’ensemble des fonctions
est l’ensemble des fonctions ![]() ,
, ![]()
où ![]() .
.
On termine en donnant l’ensemble des solutions, ou en cherchant la solution vérifiant la condition initiale donnée par l’énoncé.
1.1.3. Théorème de Cauchy-Lipschitz
Th : Si les fonctions ![]() et
et ![]() sont continues sur l’intervalle
sont continues sur l’intervalle ![]() , pour tout
, pour tout ![]() , il existe une unique solution
, il existe une unique solution ![]() de
de ![]() sur
sur ![]() vérifiant
vérifiant ![]() .
.
Elle est définie par : si ![]() ,
, ![]() avec
avec ![]() .
.
PROF DE MATHS PARTICULIER
Des cours de qualité et enseignants aguerris
Préparer des concours ou s'exercer
Avis Google France ★★★★★ 4,9 sur 5
1.2. Consignes de rédaction sur les équations différentielles
![]() a) Si nécessaire, écrire l’équation différentielle sous forme normalisée, soit
a) Si nécessaire, écrire l’équation différentielle sous forme normalisée, soit ![]() .
.
Déterminer un (ou plusieurs) intervalles ![]() sur lesquels les fonctions
sur lesquels les fonctions ![]() et
et ![]() sont continues.
sont continues.
Dans la suite, on note ![]() (resp.
(resp. ![]() ) si les fonctions
) si les fonctions ![]() et
et ![]() sont à valeurs dans
sont à valeurs dans ![]() (resp.
(resp. ![]() ) .
) .
![]() b) Noter
b) Noter ![]() .
.
Dire : on introduit ![]() une primitive de
une primitive de ![]() sur l’intervalle
sur l’intervalle ![]() .
.
La solution générale de ![]() sur
sur ![]() est la fonction
est la fonction ![]() où
où ![]() .
.
Lorsque l’équation est homogène, terminer la rédaction par :
l’ensemble des solutions de ![]() sur
sur ![]() est l’ensemble des fonctions
est l’ensemble des fonctions ![]() où
où ![]() .
.
![]() c) Lorsqu’il y a un second membre et pas de solution particulière évidente, dire :
c) Lorsqu’il y a un second membre et pas de solution particulière évidente, dire :
On cherche une solution particulière par la méthode de variation de la constante. On écrit :
![]() est solution de
est solution de ![]() sur
sur ![]()
![]()
![]()
![]() où
où ![]() est une primitive sur
est une primitive sur ![]() de
de ![]() .
.
Terminer en disant au choix :
![]() La solution générale de
La solution générale de ![]() sur
sur ![]() est définie par
est définie par ![]() ,
, ![]() où
où ![]() .
.
ou
![]() L’ ensemble des solutions de
L’ ensemble des solutions de ![]() sur
sur ![]() est l’ensemble des fonctions
est l’ensemble des fonctions ![]()
![]() où
où ![]()
ou encore
![]() L’ ensemble
L’ ensemble ![]() des solutions de
des solutions de ![]() sur
sur ![]() est égal à :
est égal à :
![]() .
.
1.3. Raccordement de solutions d’une équation différentielle
Soit ![]() .
.
![]() Supposons pour fixer les idées que
Supposons pour fixer les idées que ![]() et que
et que ![]() ne s’annule qu’en un point
ne s’annule qu’en un point ![]() de
de ![]() .
.
Si ![]() et si l’on a su déterminer les solutions de
et si l’on a su déterminer les solutions de ![]() sur
sur ![]() et sur
et sur ![]() , on pose
, on pose
![]()
où ![]() est solution de
est solution de ![]() sur
sur ![]() et
et ![]() est solution de
est solution de ![]() sur
sur ![]() .
.
![]() Puis
Puis
![]() a) on cherche s’il est possible (en choisissant éventuellement les constantes) de prolonger
a) on cherche s’il est possible (en choisissant éventuellement les constantes) de prolonger ![]() par continuité en
par continuité en ![]() , donc on cherche si la limite à gauche de
, donc on cherche si la limite à gauche de ![]() de la fonction
de la fonction ![]() est égale à la limite à droite de
est égale à la limite à droite de ![]() de
de ![]() .
.
Si c’est le cas,
![]() b) on cherche si la fonction
b) on cherche si la fonction ![]() est dérivable en
est dérivable en ![]() .
.
Si c’est le cas,
![]() c) on cherche si
c) on cherche si ![]() est encore solution de
est encore solution de ![]() en
en ![]() .
.
Dans ce cas, la (ou les) fonction(s) obtenue(s) est (sont) solution(s) de ![]() sur
sur ![]() .
.
On dit que l’on a raccordé les solutions en ![]() .
.
2- Équation différentielle linéaire vectorielle du premier ordre
2.1. Première forme
![]() où
où
![]()
![]() est un intervalle de
est un intervalle de ![]()
![]()
![]() est un
est un ![]() espace vectoriel de dimension
espace vectoriel de dimension ![]() (et
(et ![]() si
si ![]() .
.
![]()
![]() est continue
est continue
![]()
![]() est continue
est continue
et l’équation homogène associée :
![]()
Théorème de Cauchy : Si ![]() et
et ![]() , il existe une unique fonction
, il existe une unique fonction ![]() de classe
de classe ![]() sur
sur ![]() à valeurs dans
à valeurs dans ![]() vérifiant le problème de Cauchy :
vérifiant le problème de Cauchy :
![]()
De plus ![]() ,
,
![]()
Conséquence 1 : Si ![]() , l’application
, l’application ![]() est un isomorphisme d’espaces vectoriels.
est un isomorphisme d’espaces vectoriels.
Conséquence 2 : Il y a équivalence entre :
![]()
![]() est une base de l’espace vectoriel des solutions de l’équation homogène
est une base de l’espace vectoriel des solutions de l’équation homogène ![]()
![]()
![]() ,
, ![]() est une base de
est une base de ![]()
![]() il existe
il existe ![]() tel que
tel que ![]()
est une base de ![]()
2.2. Deuxième forme
![]() où
où
![]()
![]() est un intervalle de
est un intervalle de ![]()
![]()
![]()
![]()
![]() est continue
est continue
![]()
![]() est continue
est continue
et l’équation homogène associée :
![]()
C’est la traduction matricielle de la première forme.
Théorème de Cauchy :
Si ![]() et
et ![]() , il existe une unique fonction
, il existe une unique fonction ![]() de classe
de classe ![]() sur
sur ![]() à valeurs dans
à valeurs dans ![]() vérifiant le problème de Cauchy :
vérifiant le problème de Cauchy :
![]()
De plus ![]() ,
,
![]()
Conséquence 1 :
Si ![]() , l’application
, l’application ![]() est un isomorphisme d’espaces vectoriels.
est un isomorphisme d’espaces vectoriels.
Conséquence 2 :
Il y a équivalence entre :
![]()
![]() est une base de l’espace vectoriel des solutions de l’équation homogène
est une base de l’espace vectoriel des solutions de l’équation homogène ![]()
![]() si
si ![]() ,
, ![]() est une base de
est une base de ![]()
![]() il existe
il existe ![]() tel que
tel que ![]()
est une base de ![]() .
.
2.3. Résultats généraux
Avec les hypothèses de 2.1. ou 2.2.:
![]() T1 : L’ ensemble
T1 : L’ ensemble ![]() des solutions de
des solutions de ![]() est un espace vectoriel de dimension
est un espace vectoriel de dimension ![]() .
.
![]() T2 : La solution générale de
T2 : La solution générale de ![]() est la somme d’une solution particulière de
est la somme d’une solution particulière de ![]() et de la solution générale de
et de la solution générale de ![]() . C’est un espace affine.
. C’est un espace affine.
![]() T3 : Superposition des solutions
T3 : Superposition des solutions
Si 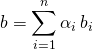 et si
et si ![]() ,
, ![]() est une solution particulière de
est une solution particulière de ![]() ,
,
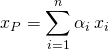 est une solution particulière de
est une solution particulière de ![]() .
.
et la traduction matricielle :
Si  et si pour tout
et si pour tout ![]() ,
, ![]() est une solution particulière de
est une solution particulière de ![]() ,
,  est une solution particulière de
est une solution particulière de ![]() .
.
2.4. Variation des constantes
![]() Équation
Équation ![]()
Hypothèse : On a pu trouver ![]() solutions
solutions ![]() de l’équation homogène
de l’équation homogène ![]() formant une base de
formant une base de ![]() .
.
On rappelle que pour tout ![]() ,
, ![]() est une base de
est une base de ![]() .
.
S’il n’y a pas de solution particulière de ![]() évidente, on utilise la méthode de variation des constantes :
évidente, on utilise la méthode de variation des constantes :
On cherche une solution particulière de la forme  en écrivant que
en écrivant que  .
.
Il suffit de décomposer ![]() dans la base
dans la base ![]() :
:  .
.
Par unicité de la décomposition de ![]() dans la base
dans la base ![]() , il suffit de trouver une solution particulière des équations si
, il suffit de trouver une solution particulière des équations si ![]() ,
, ![]() .
.
![]() Équation
Équation ![]()
Hypothèse : On a pu trouver ![]() solutions
solutions ![]() , de l’équation homogène
, de l’équation homogène ![]() formant une base de
formant une base de ![]() .S’il n’y a pas de solution particulière de
.S’il n’y a pas de solution particulière de ![]() évidente, on utilise la méthode de variation des constantes :
évidente, on utilise la méthode de variation des constantes :
On cherche une solution particulière de la forme  en écrivant que
en écrivant que ![]() .
.
Il suffit de décomposer ![]() dans la base
dans la base ![]() ,
, 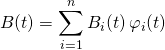 .
.
Par unicité de la décomposition de ![]() dans la base
dans la base ![]() , il suffit de trouver une solution particulière des équations :
, il suffit de trouver une solution particulière des équations : ![]() ,
, ![]() .
.
2.5. Quelques pistes de résolution
Si l’énoncé ne donne pas d’indication,
![]() Dans le cas
Dans le cas ![]() et
et ![]() , il est parfois possible en posant
, il est parfois possible en posant ![]() d’obtenir une équation différentielle linéaire du premier ordre en
d’obtenir une équation différentielle linéaire du premier ordre en ![]() que l’on sait résoudre.
que l’on sait résoudre.
![]() On peut aussi chercher s’il existe une matrice
On peut aussi chercher s’il existe une matrice ![]() (indépendante de
(indépendante de ![]() et inversible) et une matrice diagonale ou triangulaire
et inversible) et une matrice diagonale ou triangulaire ![]() telles que
telles que ![]()
et poser ![]() (on obtient alors
(on obtient alors ![]() ).
).
3. Équation  où
où 
![]() M1. Utilisation de l’exponentielle de matrices
M1. Utilisation de l’exponentielle de matrices
![]() La solution du problème de Cauchy :
La solution du problème de Cauchy : ![]() et
et ![]() est la fonction
est la fonction ![]() .
.
![]() Si
Si ![]() est une base de
est une base de ![]() , les fonctions
, les fonctions ![]() pour
pour ![]() forment une base de
forment une base de ![]() .
.
![]() M2.
M2. ![]() est une matrice dagonalisable dans
est une matrice dagonalisable dans ![]() :
:
![]() M2.1. La méthode la plus simple est de déterminer une base de vecteurs propres
M2.1. La méthode la plus simple est de déterminer une base de vecteurs propres ![]() de
de ![]() associés respectivement aux valeurs propres
associés respectivement aux valeurs propres ![]() .
.
L’ ensemble des solutions est l’ensemble des fonctions :
![]() ,
,  lorsque
lorsque ![]() décrit
décrit ![]() .
.
On peut aussi noter ![]()
et dire que ![]() est un système fondamental de solutions de
est un système fondamental de solutions de ![]() c’est-à-dire une base de l’espace vectoriel des solutions.
c’est-à-dire une base de l’espace vectoriel des solutions.
![]() M2.2. On détermine
M2.2. On détermine ![]() et
et ![]() diagonale telles que
diagonale telles que ![]() ; on pose
; on pose ![]() ; l’équation à résoudre s’écrit
; l’équation à résoudre s’écrit ![]() , ce qui donne
, ce qui donne ![]() équations linéaires scalaires d’ordre 1 (du type
équations linéaires scalaires d’ordre 1 (du type ![]() ) que l’on résout.
) que l’on résout.
Il suffit de calculer ![]() , pour obtenir
, pour obtenir ![]() . Dans ce cas, le calcul de
. Dans ce cas, le calcul de ![]() est inutile.
est inutile.
Si l’on doit de plus résoudre le problème de Cauchy ![]() et
et ![]() , il faut déterminer
, il faut déterminer ![]() pour déterminer les constantes
pour déterminer les constantes ![]() de façon à ce que
de façon à ce que ![]() ou résoudre directement le système
ou résoudre directement le système ![]() .
.
![]() M3.
M3. ![]() n’est pas diagonalisable dans
n’est pas diagonalisable dans ![]() mais est diagonalisable dans
mais est diagonalisable dans ![]() et on cherche les solutions réelles :
et on cherche les solutions réelles :
![]() a) Pour chaque valeur propre réelle
a) Pour chaque valeur propre réelle ![]() , on détermine une base du sous-espace propre
, on détermine une base du sous-espace propre ![]() .
.
![]() b) Si
b) Si ![]() est une valeur propre non réelle de
est une valeur propre non réelle de ![]() , on rappelle que si
, on rappelle que si ![]() forme une base de
forme une base de ![]() ,
, ![]() forme une base de
forme une base de ![]() .
.
![]() c) En utilisant les notations du b),
c) En utilisant les notations du b),![]()
![]()
et ![]() sont des solutions à valeurs réelles de
sont des solutions à valeurs réelles de ![]() .
.
On regroupe les solutions ainsi obtenues (en a) et c)), notées par exemple ![]() et on démontre que l’on a une famille libre.
et on démontre que l’on a une famille libre.
Pour cela, il suffit de prouver que ![]() .
.
![]() M3.
M3. ![]() est trigonalisable.
est trigonalisable.
On introduit ![]() et
et ![]() matrice triangulaire supérieure telles que
matrice triangulaire supérieure telles que ![]() , on pose
, on pose ![]() .
.
L’ équation à résoudre s’écrit ![]() , ce qui donne
, ce qui donne ![]() équations linéaires scalaires.
équations linéaires scalaires.
On résout le système « triangulaire » obtenu en commençant par la dernière équation de la forme ![]() , puis l’avant dernière
, puis l’avant dernière ![]() etc …
etc …
Il suffit de calculer ![]() pour obtenir
pour obtenir ![]() . Dans ce cas, le calcul de
. Dans ce cas, le calcul de ![]() est inutile.
est inutile.
Cas particulier : la somme des dimensions des sous-espaces propres de ![]() est égale à
est égale à ![]() .
.
Soit ![]() l’endomorphisme canoniquement associé à
l’endomorphisme canoniquement associé à ![]() et
et ![]() une famille libre de
une famille libre de ![]() vecteurs propres.
vecteurs propres.
En introduisant un vecteur ![]() tel que
tel que ![]() soit une base
soit une base ![]() de
de ![]() , la matrice
, la matrice ![]() de
de ![]() dans la base
dans la base ![]() est triangulaire supérieure.
est triangulaire supérieure.
Il est alors possible d’appliquer la méthode précédente.
4. Équation 
![]() où
où ![]() et
et ![]() .
.
![]() M1. Cas
M1. Cas ![]() .
.
Lorsque la fonction ![]() est dérivable sur l’intervalle
est dérivable sur l’intervalle ![]() de
de ![]() , la méthode la plus simple de résolution d’un système différentiel linéaire d’ordre 2 avec second membre est de chercher une équation différentielle d’ordre 2 vérifiée par
, la méthode la plus simple de résolution d’un système différentiel linéaire d’ordre 2 avec second membre est de chercher une équation différentielle d’ordre 2 vérifiée par ![]() , en déduire
, en déduire ![]() puis
puis ![]() .
.
En n’oubliant pas la réciproque !
![]() M2. Cas
M2. Cas ![]() et
et ![]() diagonalisable :
diagonalisable :
Introduire ![]() et
et ![]() diagonale telles que
diagonale telles que ![]() , poser
, poser ![]() et
et ![]() .
.
L’ équation ![]() s’écrit
s’écrit ![]() .
.
On obtient alors un système de ![]() équations du type.
équations du type.
![]() où
où ![]() .
.
Ayant résolu ce système, il reste à calculer ![]() . Dans ce cas, on doit calculer
. Dans ce cas, on doit calculer ![]() .
.
![]() M3. Cas
M3. Cas ![]() et
et ![]() trigonalisable :
trigonalisable :
Introduire ![]() et
et ![]() triangulaire telles que
triangulaire telles que ![]() , poser
, poser ![]() et
et ![]() .
.
L’ équation ![]() s’écrit
s’écrit ![]() .
.
On obtient alors un système triangulaire de ![]() équations.
équations.
On commence par résoudre ![]()
puis on « remonte ».
Ayant résolu ce système, il reste à calculer ![]() .
.
Dans ce cas, on doit calculer ![]() .
.
5. Transformer une équation différentielle scalaire d’ordre  en une équation différentielle vectorielle d’ordre 1
en une équation différentielle vectorielle d’ordre 1
Hypothèse : on suppose que ![]() est une famille de fonctions continues sur l’intervalle
est une famille de fonctions continues sur l’intervalle ![]() à valeurs dans
à valeurs dans ![]() .
.
Soit l’équation différentielle linéaire d’ordre ![]() :
: 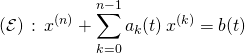 .
.
On pose
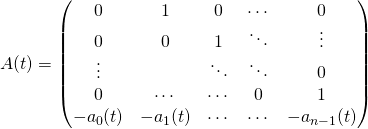

![]() est équivalente à
est équivalente à ![]() .
.
et
![]() :
: 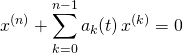
est équivalente à ![]() .
.
En particulier on peut écrire ![]() sous la forme équivalente
sous la forme équivalente ![]() avec
avec
![]() ,
, ![]() et
et ![]() .
.
Théorème de Cauchy
Si ![]() et
et ![]() sont des fonctions continues sur l’intervalle
sont des fonctions continues sur l’intervalle ![]() à valeurs dans
à valeurs dans ![]() ,
,
si ![]() et si
et si ![]()
il existe une unique fonction ![]() vérifiant le problème de Cauchy suivant :
vérifiant le problème de Cauchy suivant :
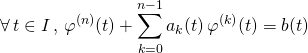
et ![]()
P1 : L’ensemble des solutions de ![]() sur
sur ![]() est un
est un ![]() espace vectoriel de dimension
espace vectoriel de dimension ![]() .
.
P2 : L’ensemble des solutions de ![]() est un espace affine : la solution générale est la somme de la solution générale de
est un espace affine : la solution générale est la somme de la solution générale de ![]() et d’une solution particulière de
et d’une solution particulière de ![]() .
.
Les étudiants de Maths Spé qui n’ont pas la possibilité de faire appel à un prof de maths particulier ou de participer à des stages intensifs de révision en Maths Sup, ont la possibilité d’utiliser différents cours en ligne de Maths en PT, ou des cours en ligne de PSI en Maths, des cours en ligne de MP en Maths ou même des cours en ligne de PC en Maths pour s’aider dans leurs révisions personnelles.
6. Résolution d’équations linaires scalaires du second ordre
6.1. Théorème de Cauchy
On cherche à déterminer les fonctions ![]() deux fois dérivables sur
deux fois dérivables sur ![]() et vérifiant
et vérifiant
![]()
![]()
où ![]() sont des fonctions continues sur l’intervalle
sont des fonctions continues sur l’intervalle ![]() à valeurs dans
à valeurs dans ![]() , la fonction
, la fonction ![]() ne s’annulant pas sur
ne s’annulant pas sur ![]() .
.
Dans le cas où ![]() sont des scalaires, on se trouve dans le cas des équations à coefficients constants étudiées au paragraphe VII.
sont des scalaires, on se trouve dans le cas des équations à coefficients constants étudiées au paragraphe VII.
En se plaçant sur un intervalle ![]() où la fonction
où la fonction ![]() ne s’annule pas, on obtient
ne s’annule pas, on obtient
l’équation homogène ![]() :
: ![]()
et l’équation complète ![]() :
: ![]() .
.
les fonctions ![]() étant continues sur
étant continues sur ![]() à valeurs dans
à valeurs dans ![]() .
.
Théorème de Cauchy :
On suppose que les fonctions ![]() sont continues sur l’intervalle
sont continues sur l’intervalle ![]() à valeurs dans
à valeurs dans ![]() .
.
Pour tout ![]() et
et ![]() , il existe une unique fonction
, il existe une unique fonction ![]() deux fois dérivable sur
deux fois dérivable sur ![]() et vérifiant le problème de Cauchy :
et vérifiant le problème de Cauchy :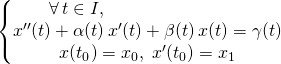
Conséquence : Pour prouver que deux solutions ![]() et
et ![]() de
de ![]() sur
sur ![]() sont égales, il suffit de trouver
sont égales, il suffit de trouver ![]() tel que
tel que ![]() et
et ![]() et utiliser ensuite l’unicité donnée par le théorème de Cauchy.
et utiliser ensuite l’unicité donnée par le théorème de Cauchy.
6.2. Équation homogène
![]() L’ ensemble des solutions de
L’ ensemble des solutions de ![]() :
: ![]() est un
est un ![]() -espace vectoriel de dimension 2.
-espace vectoriel de dimension 2.
![]() Si
Si ![]() , l’application :
, l’application :
![]() ,
, ![]()
est un isomorphisme d’espaces vectoriels.
C’est à dire si ![]() et
et ![]() , il existe une unique solution
, il existe une unique solution ![]() de
de ![]() telle que
telle que ![]() et
et ![]() .
.
![]() Si
Si ![]() et si
et si ![]() est solution de
est solution de ![]() et vérifie
et vérifie ![]() , alors
, alors ![]() , car
, car ![]() et la solution nulle vérifient le même problème de Cauchy. 🧡
et la solution nulle vérifient le même problème de Cauchy. 🧡
![]() Pour vérifier que deux solutions
Pour vérifier que deux solutions ![]() forment une base de
forment une base de ![]() , il suffit de prendre
, il suffit de prendre ![]() (le plus simple possible) et de prouver que
(le plus simple possible) et de prouver que ![]() est une base de
est une base de ![]() (il suffit de prouver que
(il suffit de prouver que ![]() )
)
et de dire que ![]() est une base de
est une base de ![]() comme image d’une base de
comme image d’une base de ![]() par l’isomorphisme
par l’isomorphisme ![]()
Si ![]() est une base de
est une base de ![]() , pour tout
, pour tout ![]()
![]() .
.
dem : il suffit de dire que pour tout ![]() est une base de
est une base de ![]() .
.
![]() Si
Si ![]() ,
,
![]() il existe un unique couple
il existe un unique couple ![]() de solutions de
de solutions de ![]() vérifiant
vérifiant
![]()
![]() .
.
![]()
![]() est une base de
est une base de ![]() , comme image de la base canonique de
, comme image de la base canonique de ![]() par l’isomorphisme
par l’isomorphisme ![]() .
.
![]() Si
Si ![]() et
et ![]() sont solutions de
sont solutions de ![]() , la fonction
, la fonction ![]() définie, pour tout
définie, pour tout ![]() , par
, par ![]() est solution de l’équation linéaire du premier ordre :
est solution de l’équation linéaire du premier ordre :
![]() . 🧡
. 🧡
6.3. Consignes de rédaction (cas de fonctions à valeurs réelles)
Si ![]() est une base de
est une base de ![]() et si
et si ![]() est une solution particulière de
est une solution particulière de ![]() conclure en disant au choix :
conclure en disant au choix :
![]() la solution générale de
la solution générale de ![]() sur
sur ![]() est définie par
est définie par
![]() ,
, ![]() où
où ![]() .
.
ou
![]() l’ensemble des solutions de
l’ensemble des solutions de ![]() sur
sur ![]() est l’ensemble des fonctions
est l’ensemble des fonctions
![]() ,
, ![]() où
où ![]() .
.
6.4. Raccordements de solutions d’une équation différentielle
Si ![]() et si l’on a su déterminer les solutions de
et si l’on a su déterminer les solutions de ![]() sur
sur ![]() et sur
et sur ![]() , on pose
, on pose
![]()
où ![]() est solution de
est solution de ![]() sur
sur ![]() et
et ![]() est solution de
est solution de ![]() sur
sur ![]() .
.
Puis
![]() a) on cherche s’il est possible (en choisissant éventuellement les constantes) de prolonger
a) on cherche s’il est possible (en choisissant éventuellement les constantes) de prolonger ![]() par continuité en
par continuité en ![]() , donc en démontrant que la limite à gauche de
, donc en démontrant que la limite à gauche de ![]() de la fonction
de la fonction ![]() est égale à la limite à droite de
est égale à la limite à droite de ![]() en
en ![]() .
.
Si c’est le cas,
![]() b) on cherche si la fonction
b) on cherche si la fonction ![]() est dérivable en
est dérivable en ![]()
… par limite du taux d’accroissement de ![]() en
en ![]()
… ou en cherchant si ![]() admet la même limite
admet la même limite ![]() à droite et à gauche en
à droite et à gauche en ![]() (dans ce cas, on rappelle que, par théorème,
(dans ce cas, on rappelle que, par théorème, ![]() est de classe
est de classe ![]() sur
sur ![]() et
et ![]() )
)
Si c’est le cas,
![]() c) on cherche si
c) on cherche si ![]() est deux fois dérivable en
est deux fois dérivable en ![]() (par limite du taux d’accroissement de
(par limite du taux d’accroissement de ![]() en
en ![]() ou grâce à la limite de
ou grâce à la limite de ![]() en c).
en c).
Si c’est le cas,
![]() d) on cherche si
d) on cherche si ![]() est encore solution de
est encore solution de ![]() en
en ![]() .
.
Dans ce cas, la (ou les) fonction(s) obtenue(s) est (sont) solution(s) de ![]() sur
sur ![]() .
.
On dit que l’on a raccordé les solutions en ![]() .
.
7. Équation linéaire du second ordre à coefficient constants
Hypothèses : soit à résoudre l’équation ![]()
où ![]() et
et ![]() est une fonction continue sur
est une fonction continue sur ![]() à valeurs dans
à valeurs dans ![]() . On note
. On note ![]() .
.
7.1. Résolution de ![]() où
où ![]() .
.
On note ![]() .
.
L’ ensemble des solutions ![]() de l’équation homogène est un espace vectoriel de dimension 2 et on note
de l’équation homogène est un espace vectoriel de dimension 2 et on note ![]() une base de
une base de ![]() .
.
Si l’équation caractéristique ![]()
![]() a deux racines distinctes
a deux racines distinctes ![]() et
et ![]() dans
dans ![]() :
:
… ![]()
![]() .
.
![]() a une racine double
a une racine double ![]() :
:
… ![]()
![]() .
.
![]() a deux racines complexes conjuguées :
a deux racines complexes conjuguées : ![]() et
et ![]() , où
, où ![]() dans le cas où
dans le cas où ![]() :
:
… ![]()
![]() .
.
![]() et pour aller plus vite dans le cas
et pour aller plus vite dans le cas ![]() avec
avec ![]() :
:
… ![]()
![]() .
.
![]() et pour aller plus vite dans le cas
et pour aller plus vite dans le cas ![]() avec
avec ![]() :
:
… ![]()
![]() .
.
ou
… ![]()
![]() .
.
Hypothèses : soit à résoudre l’équation ![]()
où ![]() et
et ![]() est une fonction continue sur
est une fonction continue sur ![]() à valeurs dans
à valeurs dans ![]() . On note
. On note ![]() .
.
7.2. Recherche d’une solution particulière de ![]() où
où ![]() .
.
![]() M1. Utilisation du principe de superposition des solutions.
M1. Utilisation du principe de superposition des solutions.
Si 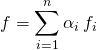 et si
et si ![]() ,
, ![]() est une solution particulière de
est une solution particulière de ![]() ,
,
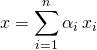 est solution de
est solution de ![]() .
.
![]() M2. Utilisation de la fonction conjuguée.
M2. Utilisation de la fonction conjuguée.
Si ![]() et si
et si ![]() ,
, ![]() est solution de
est solution de ![]() la fonction
la fonction ![]() ,
, ![]() est solution de
est solution de ![]() .
.
![]() M3. Second membre
M3. Second membre ![]() où
où ![]() est racine double de l’équation caractéristique
est racine double de l’équation caractéristique ![]() .
.
![]() On cherche une solution particulière
On cherche une solution particulière ![]() .
.
Après calculs, on obtient l’équation : ![]() .
.
![]() Cette méthode peut aussi être utilisée lorsque le second membre est de la forme
Cette méthode peut aussi être utilisée lorsque le second membre est de la forme ![]() , où
, où ![]() est racine simple de l’équation caractéris- tique
est racine simple de l’équation caractéris- tique ![]() . On obtient l’équation :
. On obtient l’équation : ![]()
et on se ramène donc à une équation linéaire scalaire du premier ordre (en posant ![]() ).
).
![]() M4. Second membre
M4. Second membre ![]() de la forme
de la forme ![]() , où
, où ![]() est une fonction polynôme et
est une fonction polynôme et ![]() .
.
On cherche une solution particulière sous la forme ![]() où
où ![]() avec
avec ![]() fonction polynôme de même degré que
fonction polynôme de même degré que ![]() et
et
![]() si
si ![]() n’est pas racine de
n’est pas racine de ![]() ,
, ![]()
![]() si
si ![]() est racine simple de
est racine simple de ![]() ,
, ![]()
![]() si
si ![]() est racine double de
est racine double de ![]() ,
, ![]()
(attention, M3 est plus simple dans ce dernier cas).
Dans cette méthode, lorsque le degré de ![]() est « élevé », il est conseillé de calculer les dérivées de
est « élevé », il est conseillé de calculer les dérivées de ![]() , puis de remplacer dans l’équation différentielle et d’introduire ensuite les coefficients de
, puis de remplacer dans l’équation différentielle et d’introduire ensuite les coefficients de ![]() .
.
![]() M4B. On peut aussi raisonner avec
M4B. On peut aussi raisonner avec ![]() et démontrer que
et démontrer que ![]() est solution de l’équation
est solution de l’équation ![]() ssi
ssi
![]() ,
, ![]()
![]()
et de trouver ensuite une solution particulière de cette équation.
![]() M5. Second membre
M5. Second membre ![]() , lorsque
, lorsque ![]() .
.
M5.1. On cherche une solution particulière sous la forme :
![]()
![]() si
si ![]() n’est pas racine du polynôme caractéristique
n’est pas racine du polynôme caractéristique ![]() .
.
![]()
![]() si
si ![]() est racine simple du polynôme caractéristique
est racine simple du polynôme caractéristique ![]() .
.
M5.2. On utilise les formules d’Euler, on cherche une solution particulière ![]() de
de ![]() ;
;
on utilise M2 pour dire que ![]() est solution particulière de
est solution particulière de ![]()
et on termine par utilisation du principe de superposition des solutions (cf M1).
En particulier, ![]() est une solution particulière de
est une solution particulière de ![]()
et ![]() est une solution particulière de
est une solution particulière de ![]() .
.
8. Quelques autres méthodes de résolutions d’équations différentielles scalaires du second ordre
8.1. Par changement de fonction inconnue
On note ![]() l’ancienne fonction,
l’ancienne fonction, ![]() la nouvelle fonction et
la nouvelle fonction et ![]() la variable. On exprime
la variable. On exprime ![]() et éventuellement
et éventuellement ![]() en fonction de
en fonction de ![]() et éventuellement
et éventuellement ![]() .
.
On remplace dans l’équation différentielle donnée. On doit obtenir une équation différentielle en ![]() de même ordre que celle dont on est parti.
de même ordre que celle dont on est parti.
On résout l’équation obtenue. Ne pas oublier à la fin de donner les solutions ![]() en utilisant la relation entre
en utilisant la relation entre ![]() et
et ![]() .
.
8.2. Méthode de Lagrange pour les équations différentielles
On suppose que l’on doit résoudre ![]() quand
quand
a) les fonctions ![]() et
et ![]() sont continues sur l’intervalle
sont continues sur l’intervalle ![]() et
et ![]() ne s’annule pas sur l’intervalle
ne s’annule pas sur l’intervalle ![]() .
.
b) on connaît une solution particulière ![]() de
de ![]() ne s’annulant pas sur
ne s’annulant pas sur ![]() .
.
On note ![]() .
.
![]() est deux fois dérivable sur
est deux fois dérivable sur ![]() ssi
ssi ![]() est deux fois dérivable sur
est deux fois dérivable sur ![]() .
.
En écrivant que ![]() est solution sur
est solution sur ![]() de
de ![]() et en utilisant le fait que
et en utilisant le fait que ![]() est solution de
est solution de ![]() , on obtient (calculs à faire) :
, on obtient (calculs à faire) :
![]() est solution sur
est solution sur ![]() de
de ![]() ssi
ssi ![]()
![]()
![]()
En posant ![]() , la fonction
, la fonction ![]() est solution sur
est solution sur ![]() de l’équation linéaire scalaire d’ordre 1 :
de l’équation linéaire scalaire d’ordre 1 :
![]()
![]()
On résout cette équation puis il reste à résoudre ![]() .
.
Important : Il vaut mieux conserver (sauf si ![]() est très simple) l’expression littérale
est très simple) l’expression littérale ![]() et on arrive à l’équation sans second membre, normalisée sous la forme,
et on arrive à l’équation sans second membre, normalisée sous la forme, ![]() .
.
Il suffit ensuite de trouver une primitive de ![]() de
de ![]() pour en déduire que
pour en déduire que ![]() est une primitive de
est une primitive de ![]() .
.
8.3. Par utilisation d’une série entière
On rédige ainsi :
On cherche une suite ![]() telle que la série entière de terme général
telle que la série entière de terme général ![]() ait un rayon de convergence
ait un rayon de convergence ![]() et telle que la fonction
et telle que la fonction ![]() définie pour tout
définie pour tout ![]() , par
, par 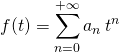 soit solution sur
soit solution sur ![]() de l’équation différentielle
de l’équation différentielle ![]() .
.
Par propriété des sommes de série entière sur l’intervalle ouvert de convergence, pour tout ![]() ,
,
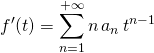 et
et  .
.
Puis
1. On écrit que ![]() est solution de
est solution de ![]() .
.
2. En utilisant l’unicité de l’écriture d’une série entière, on obtient une relation entre les coefficients ![]() .
.
3. On détermine ![]() .
.
4. On cherche le rayon de convergence ![]() .
.
5. Si possible, on calcule la somme de la série entière et éventuellement on termine la résolution de l’équation différentielle (par exemple, en utilisant la méthode de Lagrange dans le cas d’une équation linéaire du second ordre).
Cette méthode peut être utilisée lorsque les coefficients de l’équation sont des fonctions polynômes, le second membre étant une fonction polynôme ou une fonction développable en série entière.
8.4. Par changement de variable pour une équation linéaire du second ordre.
On note ![]() l’ancienne variable et
l’ancienne variable et ![]() la variable proposée par l’énoncé.
la variable proposée par l’énoncé.
![]() On suppose que
On suppose que ![]() est une bijection de classe
est une bijection de classe ![]() de l’intervalle
de l’intervalle ![]() sur l’intervalle
sur l’intervalle ![]() et que
et que ![]() .
.
![]() Alors la fonction
Alors la fonction ![]() est de classe
est de classe ![]() sur
sur ![]() .
.
![]() On écrit
On écrit ![]() soit
soit ![]() .
.
![]() La fonction
La fonction ![]() est de classe
est de classe ![]() sur
sur ![]() ssi la fonction
ssi la fonction ![]() est de classe
est de classe ![]() sur
sur ![]()
![]()
![]()
![]()
et ![]()
![]() .
.
![]() On remplace dans l’équation différentielle et on doit obtenir à la fin une équation différentielle de même ordre que celle dont on est parti, ne dépendant que de
On remplace dans l’équation différentielle et on doit obtenir à la fin une équation différentielle de même ordre que celle dont on est parti, ne dépendant que de ![]() .
.
![]() On la résout puis on détermine l’ensemble des solutions
On la résout puis on détermine l’ensemble des solutions ![]() , en utilisant le changement de variable donné.
, en utilisant le changement de variable donné.
8.5. Cas des équations d’Euler :  où
où 
![]() M1. par changement de variable :
M1. par changement de variable :
On résout l’équation sur ![]() ou
ou ![]() et on utilise le changement de variable :
et on utilise le changement de variable :
![]() ou
ou ![]() (
(![]() si l’on résout sur
si l’on résout sur ![]() et
et ![]() sinon).
sinon).
La fonction ![]() est une bijection de classe
est une bijection de classe ![]() telle que
telle que ![]() (
(![]() pour
pour ![]() et
et ![]() pour
pour ![]() ) est une bijection de classe
) est une bijection de classe ![]() .
.
On note ![]() ; on en déduit que
; on en déduit que ![]() est de classe
est de classe ![]() sur
sur ![]() , (resp
, (resp ![]() ) ssi
) ssi ![]() est de classe
est de classe ![]() sur
sur ![]() .
.
On obtient l’équation à coefficients constants :
![]()
![]()
![]() M2. On peut aussi chercher les solutions de l’équation homogène sur
M2. On peut aussi chercher les solutions de l’équation homogène sur ![]() ou
ou ![]() sous la forme
sous la forme ![]() .
.
On démontre que ![]() est solution ssi
est solution ssi ![]() .
.
Dans le cas où il y a deux solutions distinctes, on vérifie que l’on obtient une base de l’espace vectoriel des solutions ![]() .
.
8.6. En cherchant une solution particulière sous la forme d’une fonction polynôme
On commence par déterminer le degré du polynôme ![]() : en notant
: en notant ![]() , on calcule le terme de plus haut degré dans l’équation, ce qui permet d’obtenir une équation, donnant en général la valeur de
, on calcule le terme de plus haut degré dans l’équation, ce qui permet d’obtenir une équation, donnant en général la valeur de ![]() .
.
Il ne reste plus qu’à noter 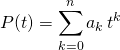 .
.
En remplaçant dans l’équation différentielle, on détermine les coefficients ![]() par résolution d’un système linéaire.
par résolution d’un système linéaire.
8.7. Méthode de la variation des constantes
On suppose que l’on connaît deux solutions ![]() et
et ![]() formant une base de l’espace vectoriel des solutions de
formant une base de l’espace vectoriel des solutions de ![]()
La méthode de variation des constantes consiste à trouver deux fonctions ![]() et
et ![]() de classe
de classe ![]() sur
sur ![]() telles que
telles que ![]() soit solution de
soit solution de
![]()
avec la condition ![]() .
.
On rappelle que les fonctions vérifient le système :
![]()
On résout le système en ![]() ,
, ![]() . Puis on détermine
. Puis on détermine ![]() et
et ![]() : comme on cherche une solution particulière, on peut choisir les constantes d’intégration de
: comme on cherche une solution particulière, on peut choisir les constantes d’intégration de ![]() et
et ![]() .
.
Exercice
Soit ![]() .
.
Résoudre l’équation ![]() où la fonction
où la fonction ![]() est continue sur l’intervalle
est continue sur l’intervalle ![]() en utilisant la méthode de variation des constantes.
en utilisant la méthode de variation des constantes.
Exercices sur les Équations différentielles linéaires en maths spé
Plan
1. Systèmes différentiels (100 mn)
2. Résolution d’équations linéaires du premier ordre (60 mn)
3. Résolution d’équations linéaires du second ordre (110mn)
4. Problèmes théoriques avec des équation du premier ordre (40 mn)
5. Problèmes théoriques avec des équations du second ordre. (180 mn)
1. Systèmes différentiels
Exercice 1
Résoudre sur ![]() l’équation
l’équation ![]() :
: ![]() avec
avec ![]()
Exercice 2
Résoudre le système ![]() avec
avec 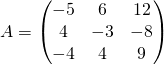 .
.
Exercice 3
Solutions réelles de ![]() avec
avec 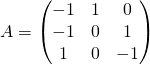 .
.
Exercice 4
Solutions réelles de ![]() et
et ![]()
2. Résolution d’équations du premier ordre
Exercice 1 Mines Ponts PC
Résoudre l’équation différentielle ![]()
Exercice 2 Centrale PSI
Soit ![]() l’équation différentielle :
l’équation différentielle : ![]() .
.
Question 1
Déterminer une relation de récurrence satisfaite par les coefficients d’une série entière ![]() dont la somme satisfait
dont la somme satisfait ![]() au voisinage de 0.
au voisinage de 0.
Question 2
Montrer que ![]() pour
pour ![]() ; minorer alors le rayon de convergence de
; minorer alors le rayon de convergence de ![]() .
.
Question 3
Exprimer à l’aide des fonctions élémentaires la solution trouvée dans la question 1.
3. Résolution d’équations d’ordre supérieur ou égal à 2
Exercice 1. CCP PC 2018
On considère l’équation différentielle ![]() :
: ![]() .
.
Question 1
Montrer que ![]() vérifie
vérifie ![]() ssi il existe
ssi il existe ![]() tel que
tel que ![]() .
.
Question 2
Résoudre l’équation ![]() .
.
Exercice 2 MinesPOnts PC
L’équation différentielle ![]() possède-t-elle des solutions bornées sur
possède-t-elle des solutions bornées sur ![]() ?
?
Exercice 3 CCP PC 2018
Résoudre sur ![]() l’équation différentielle
l’équation différentielle ![]() .
.
Exercice 4
Résoudre ![]() en cherchant une solution polynomiale.
en cherchant une solution polynomiale.
Exercice 5
Résoudre, sur tout intervalle ne contenant pas ![]() , l’équation différentielle
, l’équation différentielle ![]() en cherchant une solution de la forme
en cherchant une solution de la forme ![]() .
.
Exercice 6 Mines Ponts MP 2018
On considère l’équation différentielle ![]() .
.
Question 1
Déterminer les solutions développables en série entière.
Question 2
Quelle est la dimension de l’espace des solutions sur ![]() ?
?
Exercice 7
Résoudre sur ![]() , l’équation
, l’équation ![]() .
.
Indication : quelle est la dérivée de ![]() ?
?
4. Problèmes théoriques pour les équations d’ordre 1
Exercice 1
Soit ![]() une fonction continue de
une fonction continue de ![]() dans
dans ![]() et périodique de période 1. Montrer qu’il existe un unique réel
et périodique de période 1. Montrer qu’il existe un unique réel ![]() tel que pour toute solution non nulle
tel que pour toute solution non nulle ![]() de
de ![]() l’application
l’application ![]() soit périodique.
soit périodique.
Exercice 2
Question 1
Soit ![]() une fonction de
une fonction de ![]() dans
dans ![]() continue telle que
continue telle que ![]() . Montrer que toute solution de
. Montrer que toute solution de ![]() admet
admet ![]() pour limite en
pour limite en ![]() .
.
Question 2
Soient ![]() et
et ![]() une fonction continue de
une fonction continue de ![]() dans
dans ![]() telle que
telle que ![]() , montrer que
, montrer que ![]() .
.
5. Problèmes théoriques pour les équations d’ordre 2
Exercice 1 Mines Ponts MP 2018
Question 1 : lemme de Gronwall
Soit ![]() de classe
de classe ![]() ,
, ![]() continue et
continue et ![]() tels que pour tout
tels que pour tout ![]() ,
, ![]()
Question 2
On suppose ![]() impaire et
impaire et ![]() paire. Montrer que la fonction
paire. Montrer que la fonction ![]() solution de
solution de ![]() avec les conditions initiales
avec les conditions initiales ![]() et
et ![]() est paire.
est paire.
Montrer de même que la fonction ![]() solution de
solution de ![]() avec les conditions initiales
avec les conditions initiales ![]() et
et ![]() est impaire.
est impaire.
En déduire qu’il existe une base de l’espace des solutions de ![]() constituée d’une fonction paire et d’une fonction impaire.
constituée d’une fonction paire et d’une fonction impaire.
Question 3
On note ![]() l’ ensemble des solutions de
l’ ensemble des solutions de ![]() . On suppose que
. On suppose que ![]() admet une base
admet une base ![]() avec
avec ![]() paire et
paire et ![]() impaire.
impaire.
Montrer que ![]() est impaire et
est impaire et ![]() est paire.
est paire.
Exercice 2 Centrale 2015
Soit ![]() intégrable sur
intégrable sur ![]() .
.
Question 1
A-t-on toujours ![]() ?
?
Question 2
Soit ![]() vérifiant sur
vérifiant sur ![]() :
: ![]() .
.
Soit ![]() ,
, ![]() . Montrer que
. Montrer que ![]() est de classe
est de classe ![]() sur
sur ![]() puis que
puis que ![]() .
.
Question 3
Montrer qu’il existe ![]() tel que pour tout
tel que pour tout ![]() ,
, ![]() .
.
Question 4
Montrer que toutes les solutions sur ![]() de
de ![]() sont bornées.
sont bornées.
Exercice 3 TPE
Soit l’équation différentielle ![]() , où
, où ![]() est continue et intégrable sur
est continue et intégrable sur ![]() .
.
question 1
Montrer que si ![]() et
et ![]() sont solutions de
sont solutions de ![]() ,
, ![]() est constante.
est constante.
Question 2
Montrer que si ![]() est une solution de
est une solution de ![]() bornée sur
bornée sur ![]() ,
, ![]() admet une limite finie quand
admet une limite finie quand ![]() tend vers
tend vers ![]() , puis montrer que cette limite est nulle.
, puis montrer que cette limite est nulle.
Question 3
Montrer que ![]() admet une solution non bornée.
admet une solution non bornée.
Exercice 4
MinesPonts MP 2018 (PC 2014)
Soient ![]() continues et
continues et ![]() l’équation différentielle
l’équation différentielle ![]() .
.
Calculer pour deux solutions ![]() de
de ![]() la quantité
la quantité ![]()
Annales sur les équations différentielles linéaires en maths spé
Des annales de maths spé en mathématiques sont disponibles via la rubrique Annales.
Divers cours en ligne de maths pour les maths spé sont consultables totalement gratuitement. Que ce soit pour une légère remise à niveau ou pour combler un tout petit oubli, les cours en ligne sont toujours utiles. Découvrez quelques autres cours de maths au programme :

