Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Espaces Euclidiens pour les MP, PC, PSI et PT
Résumé de cours Exercices Annales
Résumé de cours et méthodes – Espaces Euclidiens
Plan
On suppose que ![]() est un espace euclidien.
est un espace euclidien.
1. Rappel des propriétés du produit scalaire dans un espace vectoriel euclidien ![]() .
.
2. Utilisation du produit vectoriel.
3. Caractérisation des isométries et des matrices orthogonales.
4. Matrices orthogonales d’ordre 2.
5. Matrices orthogonales d’ordre 3.
6. Endomorphismes symétriques.
7. Endomorphismes symétriques positifs (exercices).
1. Rappel des propriétés du produit scalaire dans un espace vectoriel euclidien  .
.
![]() M1. Utilisation d’une base orthonormale
M1. Utilisation d’une base orthonormale ![]() ,
,
![]()
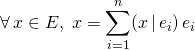 .
.
![]()
![]() ,
,
![]() et
et 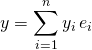 , alors
, alors 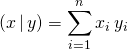 et
et 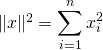 .
.
![]() Si l’on note
Si l’on note ![]() et
et ![]() les matrices colonnes de
les matrices colonnes de ![]() et
et ![]() dans la base
dans la base ![]() ,
, ![]() .
.
![]() M2. Si
M2. Si ![]() est une base orthonormale de l’espace euclidien
est une base orthonormale de l’espace euclidien ![]() et si
et si ![]() où
où ![]() ,
, ![]() (à redémontrer).
(à redémontrer).
![]() M3. Si
M3. Si ![]() est un produit scalaire sur l’espace vectoriel euclidien
est un produit scalaire sur l’espace vectoriel euclidien ![]() de base
de base ![]() , on peut définir la matrice
, on peut définir la matrice ![]() où
où ![]() ,
,
(on dit que ![]() est la matrice du produit scalaire
est la matrice du produit scalaire ![]() dans la base
dans la base ![]() ).
).
En notant ![]() et
et ![]() ,
,
![]() .
.
![]() M4. Si
M4. Si ![]() est une forme linéaire sur l’espace euclidien
est une forme linéaire sur l’espace euclidien ![]() , il existe un unique vecteur
, il existe un unique vecteur ![]() tel que
tel que ![]() .
.
Exercice :
Soit ![]() et
et ![]() une forme linéaire sur
une forme linéaire sur ![]() . Il existe une unique matrice
. Il existe une unique matrice ![]() telle que
telle que ![]() .
.
2. Utilisation du produit vectoriel
![]() P1
P1 ![]() est une application bilinéaire définie sur
est une application bilinéaire définie sur ![]() à valeurs dans
à valeurs dans ![]() vérifiant :
vérifiant :
![]()
![]() .
.
![]()
![]() si, et seulement si, la famille
si, et seulement si, la famille ![]() est liée.
est liée.
![]()
![]() .
.
![]() la famille
la famille ![]() est libre ssi
est libre ssi ![]() est une base directe de
est une base directe de ![]()
![]() P2 Identité de Lagrange :
P2 Identité de Lagrange : ![]()
![]() .
.
![]() P3 Si
P3 Si ![]() et
et ![]() sont deux vecteurs non nuls :
sont deux vecteurs non nuls : ![]() , où
, où ![]() est la mesure de l’angle de vecteurs
est la mesure de l’angle de vecteurs ![]() et
et ![]()
![]() vérifie
vérifie ![]() .
.
![]() P4 interprétation du produit mixte lorsque
P4 interprétation du produit mixte lorsque ![]() et
et ![]() forment une famille libre :
forment une famille libre :
![]() est égal au volume du parallélépipède construit sur les vecteurs
est égal au volume du parallélépipède construit sur les vecteurs ![]() et
et ![]() .
.
![]() est égal à 6 fois le volume du tétraèdre construit sur les vecteurs
est égal à 6 fois le volume du tétraèdre construit sur les vecteurs ![]() et
et ![]() .
.
![]() P5 Si
P5 Si ![]() est une base orthonormale directe de l’espace vectoriel euclidien orienté de dimension 3 :
est une base orthonormale directe de l’espace vectoriel euclidien orienté de dimension 3 :
![]()
![]() ,
, ![]() et
et ![]() .
.
![]() si
si ![]() et
et ![]() ,
,
![]() est égal à
est égal à ![]()
![]() P6 double produit vectoriel :
P6 double produit vectoriel :
Pour tous vecteurs ![]() et
et ![]() de
de ![]() ,
,
![]()
et ![]() .
.
Pour retenir la formule : vecteur du milieu multiplié par le produit scalaire des deux autres moins le produit du vecteur restant dans la parenthèse multiplié par le produit scalaire des deux autres.
3. Caractérisation des isométries et des matrices orthogonales
![]() Si
Si ![]() est un espace vectoriel euclidien de dimension
est un espace vectoriel euclidien de dimension ![]() et si
et si ![]() , il y a équivalence entre :
, il y a équivalence entre :
1. ![]() est une isométrie (ou un automorphisme orthogonal),
est une isométrie (ou un automorphisme orthogonal),
2. ![]()
![]() ,
,
3. ![]() ,
,
4. pour toute base orthonormale ![]() de
de ![]()
![]() est une base orthonormale de
est une base orthonormale de ![]() ,
,
5. il existe une base orthonormale ![]() de
de ![]() telle que
telle que ![]() soit une base orthonormale de
soit une base orthonormale de ![]() ,
,
6. la matrice de ![]() dans une base orthonormale est une matrice orthogonale.
dans une base orthonormale est une matrice orthogonale.
![]() On note
On note ![]() l’ensemble des isométries de
l’ensemble des isométries de ![]() ,
, ![]() est un sous-groupe de
est un sous-groupe de ![]() appelé groupe orthogonal de
appelé groupe orthogonal de ![]() .
.
![]() Si
Si ![]() est une isométrie,
est une isométrie, ![]() .
.
![]() On note
On note ![]() l’ensemble des rotations de
l’ensemble des rotations de ![]() (isométries de
(isométries de ![]() de déterminant égal à 1),
de déterminant égal à 1), ![]() est un sous-groupe de
est un sous-groupe de ![]() appelé groupe spécial orthogonal de
appelé groupe spécial orthogonal de ![]() .
.
![]() n’implique pas que
n’implique pas que ![]() est une isométrie.
est une isométrie.
![]() Si
Si ![]() et si
et si ![]() est le système de ses vecteurs colonnes, il y a équivalence entre :
est le système de ses vecteurs colonnes, il y a équivalence entre :
1. ![]() est une matrice orthogonale,
est une matrice orthogonale,
2. ![]() ,
,
3. ![]() ,
,
4. ![]() ,
,
5. ![]() est une base orthonormale de l’espace vectoriel euclidien
est une base orthonormale de l’espace vectoriel euclidien ![]() pour la structure euclidienne canonique,
pour la structure euclidienne canonique,
6. ![]() ,
,
7. ![]() est la matrice d’une isométrie de
est la matrice d’une isométrie de ![]() , espace euclidien de dimension
, espace euclidien de dimension ![]() , dans une base orthonormale.
, dans une base orthonormale.
![]() On note
On note ![]() l’ensemble des matrices orthogonales d’ordre
l’ensemble des matrices orthogonales d’ordre ![]() .
.
![]() est un sous-groupe de
est un sous-groupe de ![]() appelé groupe orthogonal d’ordre
appelé groupe orthogonal d’ordre ![]() .
.
![]() Si
Si ![]() ,
, ![]() .
.
![]()
![]() est un sous-groupe de
est un sous-groupe de ![]() noté
noté ![]() et appelé groupe spécial orthogonal d’ordre
et appelé groupe spécial orthogonal d’ordre ![]() .
.
![]() n’implique pas que
n’implique pas que ![]() est une matrice orthogonale.
est une matrice orthogonale.
![]() À savoir redémontrer :
À savoir redémontrer :
![]() 1. Si
1. Si ![]() est un espace euclidien et
est un espace euclidien et ![]() ,
, ![]() .
.
![]() 2. Si
2. Si ![]() ,
, ![]() .
.
![]() 3. Si
3. Si ![]() ,
, ![]() .
.
![]() 4.
4. ![]() est une partie compacte de
est une partie compacte de ![]() .
.
![]() Réduction d’une isométrie :
Réduction d’une isométrie :
Soient ![]() un espace euclidien et
un espace euclidien et ![]() une isométrie.
une isométrie.
Il existe une base orthonormale dans laquelle la matrice de ![]() est diagonale par blocs, les blocs étant de la forme
est diagonale par blocs, les blocs étant de la forme ![]()
![]() et
et ![]() où
où ![]() .
.
![]() Réduction d’une matrice orthogonale :
Réduction d’une matrice orthogonale :
Toute matrice orthogonale est orthogonalement semblable à une matrice diagonale par blocs, les blocs étant de la forme ![]() ,
, ![]() et
et ![]() où
où ![]() .
.
COURS DE MATHS A DOMICILE
Les meilleurs profs de maths pour
réussir sa scolarité
En ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
4. Matrices orthogonales d’ordre 2
P1 : Toute matrice de ![]() s’écrit
s’écrit
![]()
![]() si son déterminant est égal à
si son déterminant est égal à ![]() .
.
![]()
![]() si son déterminant est égal à
si son déterminant est égal à ![]() .
.
P2 : ![]()
![]() est un groupe commutatif.
est un groupe commutatif.
Pour tout ![]() ,
,
![]()
![]() et
et ![]() .
.
![]()
![]() .
.
P3 : Soit ![]() un plan euclidien orienté et
un plan euclidien orienté et ![]() , il existe un unique réel
, il existe un unique réel ![]() de
de ![]() tel que la matrice de
tel que la matrice de ![]() dans toute base orthonormale directe de
dans toute base orthonormale directe de ![]() s’écrive
s’écrive ![]() .
.
On dit que ![]() est une rotation d’angle de mesure
est une rotation d’angle de mesure ![]() .
.
P4 : Si ![]() est une rotation du plan euclidien orienté
est une rotation du plan euclidien orienté ![]() , on détermine une mesure de l’angle
, on détermine une mesure de l’angle ![]() de la rotation
de la rotation ![]() en introduisant un vecteur unitaire
en introduisant un vecteur unitaire ![]() et en résolvant
et en résolvant
![]() et
et ![]()
(![]() est le produit mixte de
est le produit mixte de ![]() et
et ![]() soit le déterminant de
soit le déterminant de ![]() dans une base orthonormale directe).
dans une base orthonormale directe).
P5 : Si ![]() est une isométrie du plan euclidien
est une isométrie du plan euclidien ![]() de déterminant égal à
de déterminant égal à ![]() , il existe un réel
, il existe un réel ![]() tel que la matrice de
tel que la matrice de ![]() dans une base orthonormale soit
dans une base orthonormale soit ![]() .
. ![]() est alors la réflexion, i.e. la symétrie orthogonale par rapport à
est alors la réflexion, i.e. la symétrie orthogonale par rapport à ![]() où
où ![]() est un vecteur directeur de la droite
est un vecteur directeur de la droite ![]()
5. Matrices orthogonales d’ordre 3
5.1. Réduction en base orthonormale d’une isométrie
![]() P1 : Si
P1 : Si ![]() est une isométrie d’un espace euclidien
est une isométrie d’un espace euclidien ![]() de dimension 3, il existe une base orthonormale
de dimension 3, il existe une base orthonormale ![]() de
de ![]() et un réel
et un réel ![]() tels que la matrice de
tels que la matrice de ![]() dans la base
dans la base ![]() s’écrive :
s’écrive :
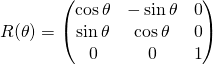
ou 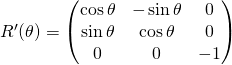 .
.
![]() P2 : Si
P2 : Si ![]() , il existe une matrice
, il existe une matrice ![]() orthogonale d’ordre 3 et un réel
orthogonale d’ordre 3 et un réel ![]() tels que
tels que
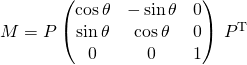
ou 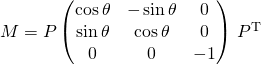 .
.
Remarque : on peut supposer que la base ![]() du premier résultat est orthonormale directe (si
du premier résultat est orthonormale directe (si ![]() n’est pas orthonormale directe,
n’est pas orthonormale directe, ![]() est directe et la matrice de
est directe et la matrice de ![]() dans
dans ![]() est égale à la matrice de
est égale à la matrice de ![]() dans la base
dans la base ![]() .)
.)
On peut donc aussi supposer que ![]() est une matrice orthogonale directe dans le résultat 2).
est une matrice orthogonale directe dans le résultat 2).
Les résultats résumés ci-dessous sont développés dans les différents paragraphes qui suivent :
![]() 1er cas : matrice
1er cas : matrice ![]()
![]() 1er sous-cas :
1er sous-cas : ![]() ,
,
![]() ,
, ![]() .
.
![]() 2ème sous-cas :
2ème sous-cas : ![]() où
où ![]() ,
,
![]() est une symétrie orthogonale par rapport à
est une symétrie orthogonale par rapport à ![]() (cf §5.2.).
(cf §5.2.).
![]() est symétrique de déterminant égal à 1.
est symétrique de déterminant égal à 1.
On peut aussi dire que ![]() est une rotation d’axe dirigé par
est une rotation d’axe dirigé par ![]() et d’angle
et d’angle ![]() .
.
![]() 3ème sous-cas :
3ème sous-cas : ![]() et
et ![]() est une base directe,
est une base directe,
![]() est une rotation d’axe dirigé par
est une rotation d’axe dirigé par ![]() et d’angle
et d’angle ![]() (cf § 5.3.).
(cf § 5.3.).
![]() 2ème cas matrice
2ème cas matrice ![]()
![]() 1er sous-cas :
1er sous-cas : ![]()
![]() est une réflexion par rapport à
est une réflexion par rapport à ![]() (cf §5.2.).
(cf §5.2.).
![]() est symétrique de déterminant égal à
est symétrique de déterminant égal à ![]() .
.
![]() 2ème sous-cas :
2ème sous-cas : ![]() où
où ![]()
![]() ,
, ![]() .
.
![]() 3ème sous-cas :
3ème sous-cas : ![]() et
et ![]() est une base directe
est une base directe
h.p : ![]() est une anti-rotation (cf § 5.4.).
est une anti-rotation (cf § 5.4.).
5.2. Matrices orthogonales et symétriques
![]() M1. Interprétation d’une matrice orthogonale d’ordre 3 et symétrique.
M1. Interprétation d’une matrice orthogonale d’ordre 3 et symétrique.
Si ![]() et si
et si ![]() ,
, ![]() est la matrice d’une symétrie orthogonale notée
est la matrice d’une symétrie orthogonale notée ![]() .
.
Dans le cas où ![]() ,
,
![]() si
si ![]() ,
, ![]() est une réflexion c’est-à-dire une symétrie telle que les sous espaces vectoriels
est une réflexion c’est-à-dire une symétrie telle que les sous espaces vectoriels ![]() et
et ![]() sont des supplémentaires orthogonaux et
sont des supplémentaires orthogonaux et ![]() .
.
La résolution de l’équation ![]() donne l’équation d’un plan
donne l’équation d’un plan ![]() et on détermine un vecteur
et on détermine un vecteur ![]() orthogonal à ce plan
orthogonal à ce plan ![]() .
.
![]() est la réflexion par rapport au plan
est la réflexion par rapport au plan ![]() .
.
![]() si
si ![]() ,
, ![]() est un retournement ou demi-tour (une symétrie telle que
est un retournement ou demi-tour (une symétrie telle que ![]() et
et ![]() sont des sous espaces supplémentaires orthogonaux et
sont des sous espaces supplémentaires orthogonaux et ![]() ).
).
En résolvant ![]() , on obtient l’équation d’un plan
, on obtient l’équation d’un plan ![]() , on détermine un vecteur
, on détermine un vecteur ![]() orthogonal à ce plan
orthogonal à ce plan ![]() .
.
![]() est le demi-tour par rapport à la droite
est le demi-tour par rapport à la droite ![]() .
.
Remarque :
![]() est la réflexion par rapport au plan
est la réflexion par rapport au plan ![]() ssi
ssi ![]() est le retournement par rapport à la droite
est le retournement par rapport à la droite ![]() .
.
![]() M2. On se place ici dans un espace euclidien de dimension
M2. On se place ici dans un espace euclidien de dimension ![]()
Écriture matricielle d’une symétrie orthogonale (c’est-à-dire une symétrie telle que les sous-espaces vectoriels ![]() et
et ![]() sont des supplémentaires orthogonaux. On suppose ici que
sont des supplémentaires orthogonaux. On suppose ici que ![]() .
.
![]() M2.1. Traduction de la symétrie orthogonale
M2.1. Traduction de la symétrie orthogonale ![]() par rapport à la droite
par rapport à la droite ![]() où
où ![]() .
.
La projection orthogonale ![]() sur
sur ![]() est définie par
est définie par ![]() , la symétrie
, la symétrie ![]() vérifie
vérifie ![]() , soit
, soit ![]() .
.
Si ![]() est la matrice de
est la matrice de ![]() dans une base orthonormale
dans une base orthonormale ![]() , on peut démontrer que la matrice de
, on peut démontrer que la matrice de ![]() dans la base
dans la base ![]() est
est ![]() .
.
![]() M2.2. Traduction de la réflexion
M2.2. Traduction de la réflexion ![]() par rapport à l’hyperplan
par rapport à l’hyperplan ![]() où
où ![]() est un vecteur unitaire :
est un vecteur unitaire :
La projection orthogonale ![]() sur
sur ![]() est définie par
est définie par ![]() ,
,
la projection orthogonale ![]() sur
sur ![]() est définie par
est définie par ![]() .
.
La symétrie par rapport à ![]() est définie par
est définie par ![]()
![]() , soit
, soit ![]() .
.
Lorsque ![]() est la matrice de
est la matrice de ![]() dans une base orthonormale
dans une base orthonormale ![]() , la matrice de la réflexion
, la matrice de la réflexion ![]() dans la base
dans la base ![]() est égale à
est égale à![]() (à démontrer).
(à démontrer).
On pourra s’aider du dessin suivant pour la réflexion par rapport à ![]() .
.
5.3. Matrices de rotation
Dans ce paragraphe, on considère que ![]() est un espace euclidien orienté de dimension 3.
est un espace euclidien orienté de dimension 3.
![]() M1. Si
M1. Si ![]() est une base orthonormale directe de
est une base orthonormale directe de ![]() , la matrice de la rotation
, la matrice de la rotation ![]() d’axe dirigé par le vecteur
d’axe dirigé par le vecteur ![]() et d’angle de mesure
et d’angle de mesure ![]() dans la base
dans la base ![]() est
est 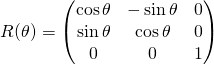 .
.
De plus, si ![]()
![]() . (sauf MP)
. (sauf MP)
![]() M2. Soit
M2. Soit ![]() la matrice d’une rotation
la matrice d’une rotation ![]()
![]() 1- Si
1- Si ![]() est une mesure de l’angle de la rotation :
est une mesure de l’angle de la rotation : ![]() .
.
![]() 2- On détermine un vecteur unitaire
2- On détermine un vecteur unitaire ![]() de l’axe de la rotation en résolvant
de l’axe de la rotation en résolvant ![]() (soit
(soit ![]() ).
).
![]() 3- On détermine le signe de
3- On détermine le signe de ![]() en prenant
en prenant ![]() et en utilisant
et en utilisant ![]() a même signe que le produit mixte
a même signe que le produit mixte ![]() .
.
en effet ![]() .
.
exercice
Soit 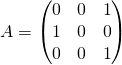 . Caractériser l’endomorphisme
. Caractériser l’endomorphisme ![]() canoniquement associé.
canoniquement associé.
![]() M3. Pour écrire la matrice de la rotation
M3. Pour écrire la matrice de la rotation ![]() d’axe dirigée par le vecteur unitaire
d’axe dirigée par le vecteur unitaire ![]() et d’angle
et d’angle ![]() , on introduit un vecteur
, on introduit un vecteur ![]() unitaire tel que
unitaire tel que ![]() . On détermine
. On détermine ![]() tel que
tel que ![]() soit une base orthonormale directe. Dans cette base, la matrice
soit une base orthonormale directe. Dans cette base, la matrice ![]() de
de ![]() est la matrice écrite dans M1, puis en introduisant
est la matrice écrite dans M1, puis en introduisant ![]() la matrice de passage de la base orthonormale directe de l’énoncé à la base
la matrice de passage de la base orthonormale directe de l’énoncé à la base ![]() ,
, ![]() par la formule de changement de bases.
par la formule de changement de bases.
(h.p. : ![]() ).
).
Exercice :
Ecrire la matrice de la rotation de ![]() d’axe dirigé par
d’axe dirigé par ![]() et d’angle de mesure
et d’angle de mesure ![]() dans la base canonique de
dans la base canonique de ![]() .
.
5.4. Matrices d’anti-rotation (h.p.)
Dans ce paragraphe, on considère que ![]() est un espace euclidien orienté de dimension 3.
est un espace euclidien orienté de dimension 3.
Soit une base orthonormale directe ![]() .
.
On suppose que ![]() est une isométrie dont la matrice dans
est une isométrie dont la matrice dans ![]() est
est 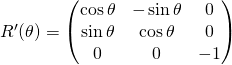 .
.
avec ![]() .
.
![]() est égale aux deux produits :
est égale aux deux produits :
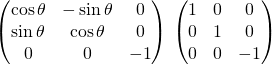 .
.
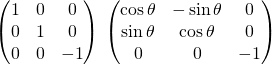 .
.
alors ![]() où
où ![]() est la rotation d’axe dirigé par
est la rotation d’axe dirigé par ![]() et d’angle
et d’angle ![]() et
et ![]() est la réflexion par rapport au plan
est la réflexion par rapport au plan ![]() .
.
6. Endomorphismes symétriques
6.1. Résultats généraux
D : Un endomorphisme ![]() de l’espace euclidien
de l’espace euclidien ![]() est symétrique ssi
est symétrique ssi ![]() .
.
P1 : L’ensemble des endomorphismes symétriques de l’espace euclidien ![]() est un sous-espace vectoriel de
est un sous-espace vectoriel de ![]() noté
noté ![]() .
.
P2 : Soit ![]() est un espace euclidien et
est un espace euclidien et ![]() .
.
Il y a équivalence entre :
![]()
![]() est un endomorphisme symétrique de
est un endomorphisme symétrique de ![]() .
.
![]() pour toute base orthonormale
pour toute base orthonormale ![]() de
de ![]() la matrice de
la matrice de ![]() dans la base
dans la base ![]() est une matrice symétrique,
est une matrice symétrique,
![]() il existe une base orthonormale
il existe une base orthonormale ![]() de
de ![]() dans laquelle la matrice de
dans laquelle la matrice de ![]() est une matrice symétrique.
est une matrice symétrique.
P3 : Si ![]() est un espace euclidien de dimension
est un espace euclidien de dimension ![]() ,
, ![]() .
.
P4 : Si ![]() est un endomorphisme symétrique de
est un endomorphisme symétrique de ![]() ,
, ![]() et
et ![]() sont des supplémentaires orthogonaux. 🧡
sont des supplémentaires orthogonaux. 🧡
Pour maximiser vos chances de réussite aux concours post-prépa, les cours en ligne de Maths en PSI, les cours en ligne de Maths en PC et les cours en ligne de Maths en MP tout comme les cours en ligne de Maths en PT sont de très bons supports qui vous permettent de vérifier si vous connaissez bien les notions essentielles de chaque cours.
6.2. Réduction
![]() LE théorème (dit aussi théorème spectral) :
LE théorème (dit aussi théorème spectral) :
Si ![]() est un endomorphisme symétrique de l’espace vectoriel euclidien
est un endomorphisme symétrique de l’espace vectoriel euclidien ![]() de dimension
de dimension ![]() , il existe une base orthonormale de
, il existe une base orthonormale de ![]() formée de vecteurs propres de
formée de vecteurs propres de ![]() .
.
![]() est somme directe des sous-espaces propres de
est somme directe des sous-espaces propres de ![]() qui sont deux à deux orthogonaux.
qui sont deux à deux orthogonaux.
![]() La traduction matricielle : soit
La traduction matricielle : soit ![]() , il existe une matrice
, il existe une matrice ![]() diagonale et une matrice
diagonale et une matrice ![]() orthogonale d’ordre
orthogonale d’ordre ![]() telles que
telles que ![]() .
.
Conséquences :
![]() Si l’on demande de diagonaliser un endomorphisme
Si l’on demande de diagonaliser un endomorphisme ![]() d’un espace vectoriel euclidien
d’un espace vectoriel euclidien ![]() , il faut commencer par se demander si
, il faut commencer par se demander si ![]() est un endomorphisme symétrique.
est un endomorphisme symétrique.
![]() Pour effectuer des raisonnements sur un endomorphisme symétrique
Pour effectuer des raisonnements sur un endomorphisme symétrique ![]() , il peut être intéressant d’introduire une base orthonormale
, il peut être intéressant d’introduire une base orthonormale ![]() de vecteurs propres de
de vecteurs propres de ![]() .
.
![]() Pour prouver des propriétés de
Pour prouver des propriétés de ![]() symétrique réelle, il est en général utile de simplifier les calculs en écrivant
symétrique réelle, il est en général utile de simplifier les calculs en écrivant ![]() où
où ![]() est diagonale et
est diagonale et ![]() orthogonale.
orthogonale.
![]() Méthode de réduction d’une matrice symétrique réelle
Méthode de réduction d’une matrice symétrique réelle ![]() (d’ordre
(d’ordre ![]() )
)
![]() a) Commencer par dire qu’elle est diagonalisable et qu’il existe une matrice
a) Commencer par dire qu’elle est diagonalisable et qu’il existe une matrice ![]() orthogonale telle que
orthogonale telle que ![]() soit diagonale.
soit diagonale.
![]() b) Déterminer
b) Déterminer ![]() (en général par calcul de
(en général par calcul de ![]() ).
).
![]() c) Déterminer une base orthonormale de vecteurs propres de
c) Déterminer une base orthonormale de vecteurs propres de ![]() , pour obtenir
, pour obtenir ![]() orthogonale.
orthogonale.
i) Si ![]() a
a ![]() valeurs propres distinctes, il suffit de déterminer une base de vecteurs propres et de normer chacun de ces vecteurs.
valeurs propres distinctes, il suffit de déterminer une base de vecteurs propres et de normer chacun de ces vecteurs.
ii) Si ![]() a au moins une valeur propre multiple, pour chacune des valeurs propres multiples
a au moins une valeur propre multiple, pour chacune des valeurs propres multiples ![]() , il sera nécessaire de déterminer une base orthonormale du sous-espace propre.
, il sera nécessaire de déterminer une base orthonormale du sous-espace propre.
On peut commencer par déterminer une base de ![]() puis on peut l’orthonormaliser par le principe d’orthonormalisation de Gram-Schmidt.
puis on peut l’orthonormaliser par le principe d’orthonormalisation de Gram-Schmidt.
Cas particulier : ![]() a une valeur propre double
a une valeur propre double ![]() et une valeur propre simple
et une valeur propre simple ![]() .
.
Soit ![]() l’endomorphisme canonique- ment associé à
l’endomorphisme canonique- ment associé à ![]() .
.
Dans ce cas, ![]() où
où ![]() et
et ![]() .
.
![]() En traduisant
En traduisant ![]() , on obtient une équation de plan de la forme
, on obtient une équation de plan de la forme ![]() .
.
![]()
![]() .
.
On en déduit ![]() tel que
tel que ![]() et
et ![]() .
.
![]() On introduit
On introduit ![]() tel que
tel que ![]() et
et ![]() , alors
, alors ![]() car
car ![]() .
.
![]() Soit
Soit ![]() non colinéaire à
non colinéaire à ![]() . Par le procédé d’orthonormalisation de Gram-Schmidt, on détermine une base orthonormale
. Par le procédé d’orthonormalisation de Gram-Schmidt, on détermine une base orthonormale ![]() de
de ![]() .
.
Alors ![]() est une base orthonormale de vecteurs propres de
est une base orthonormale de vecteurs propres de ![]() .
.
h.p. en utilisant le produit vectoriel, (c’est plus rapide) :
![]() On introduit
On introduit ![]() tel que
tel que ![]() et
et ![]() , alors
, alors ![]() car
car ![]() .
.
![]() Soit
Soit ![]() .
. ![]() est une base orthonormale. On vérifie que
est une base orthonormale. On vérifie que ![]() .
.
Alors ![]() est une base orthonormale de vecteurs propres de
est une base orthonormale de vecteurs propres de ![]() .
.
6.3. Projecteurs orthogonaux, symétries orthogonales
Résultats à savoir démontrer
Def : un projecteur ![]() est dit orthogonal lorsque
est dit orthogonal lorsque ![]() et
et ![]() sont orthogonaux.
sont orthogonaux.
R1 : Soit ![]() un espace euclidien et
un espace euclidien et ![]() un projecteur de
un projecteur de ![]() .
. ![]() est un projecteur orthogonal si, et seulement si,
est un projecteur orthogonal si, et seulement si, ![]() est un endomorphisme symétrique. ( au programme en MP)
est un endomorphisme symétrique. ( au programme en MP)
R2 : Soit ![]() un espace euclidien et
un espace euclidien et ![]() une symétrie de
une symétrie de ![]() différente de
différente de ![]() . Il y a équivalence entre :
. Il y a équivalence entre :
a) ![]() est une isométrie
est une isométrie
b) ![]() est un endomorphisme symétrique
est un endomorphisme symétrique
c) les sous espaces ![]() et
et ![]() sont des supplémentaires orthogonaux.
sont des supplémentaires orthogonaux.
On dit que ![]() est une symétrie orthogonale.
est une symétrie orthogonale.
7. Endomorphismes symétriques positifs (exercices)
7.1. Raisonnements sur les endomorphismes
Soit ![]() un espace euclidien.
un espace euclidien.
Un endomorphisme ![]() symétrique de
symétrique de ![]() est dit positif si
est dit positif si ![]() ,
, ![]() .
.
Un endomorphisme ![]() symétrique de
symétrique de ![]() est dit défini positif si
est dit défini positif si
![]() ,
, ![]() .
.
Exercice 1
Soit ![]() un endomorphisme symétrique de
un endomorphisme symétrique de ![]() . Montrer que :
. Montrer que :
![]() est positif ssi
est positif ssi ![]() ;
;
![]() est défini positif ssi
est défini positif ssi ![]() .
.
Exercice 2
Soit ![]() un endomorphisme symétrique positif. Il existe un endomorphisme symétrique
un endomorphisme symétrique positif. Il existe un endomorphisme symétrique ![]() positif tel que
positif tel que ![]() .
.
![]() est unique.
est unique.
7.2. Raisonnements sur les matrices
Soit ![]() .
.
![]() est dite positive ssi
est dite positive ssi ![]() .
.
![]() est dite définie positive ssi
est dite définie positive ssi ![]() .
.
On note ![]() l’ensemble des matrices symétriques réelles positives et
l’ensemble des matrices symétriques réelles positives et ![]() l’ensemble des matrices symétriques réelles définies positives.
l’ensemble des matrices symétriques réelles définies positives.
Exercice 3
Montrer que
![]()
et ![]() .
.
Exercice 4
a) Si ![]() , la matrice
, la matrice ![]() est une matrice symétrique positive.
est une matrice symétrique positive.
b) Si ![]() , la matrice
, la matrice ![]() est une matrice symétrique définie positive.
est une matrice symétrique définie positive.
Exercice 5
Si ![]() est une matrice symétrique positive, il existe
est une matrice symétrique positive, il existe ![]() symétrique positive telle que
symétrique positive telle que ![]() .
.
Exercice 6
Soit ![]() et
et ![]() l’endomorphisme canoniquement associé à
l’endomorphisme canoniquement associé à ![]() .
.
![]() est un endomorphisme symétrique positif (resp. défini positif) ssi
est un endomorphisme symétrique positif (resp. défini positif) ssi ![]() est une matrice symétrique positive (resp. définie positive).
est une matrice symétrique positive (resp. définie positive).
Les deux points de vue ont été développés de façon indépendante de façon à pouvoir être utilisés dans un devoir.
Exercices sur les espaces euclidiens en maths spé
Plan
1. Famille libre de matrices de rang 1 (25 mn)
2. Sur les projections orthogonales (60 mn)
3. Base orthonormale et distance à un s.e.v. (15 mn)
4. Caractérisation de sous-espaces orthogonaux en termes de distances. (30 mn)
5. Endomorphisme 1-lipschitzien d’un espace euclidien (30 mn)
6. Matrice telle que ![]() (40 mn).
(40 mn).
1. Famille libre de matrices de rang 1
Soient ![]() et
et ![]() .
.
Soient ![]() et
et ![]() deux familles libres de
deux familles libres de ![]() .
.
La famille ![]() est une famille libre de
est une famille libre de ![]() formée de matrices de rang 1. Vrai ou Faux ?
formée de matrices de rang 1. Vrai ou Faux ?
Question 2
Si ![]() est une base orthonormale de
est une base orthonormale de ![]() pour le produit scalaire usuel,
pour le produit scalaire usuel, ![]() est une base orthonormale de
est une base orthonormale de ![]() muni du produit scalaire usuel noté
muni du produit scalaire usuel noté ![]() .
.
2. Sur les projections orthogonales
Question 1
Soit ![]() un sous-espace vectoriel de dimension finie du préhilbertien
un sous-espace vectoriel de dimension finie du préhilbertien ![]() et
et ![]() la projection orthogonale sur
la projection orthogonale sur ![]() .
.
a) ![]()
b) Pour tout ![]()
c) ![]() vérifie
vérifie ![]()
Question 2
Soient ![]() et
et ![]() deux sous-espaces vectoriels de dimension finie.
deux sous-espaces vectoriels de dimension finie.
On suppose que ![]() .
.
a) Caractériser ![]() .
.
b) On suppose toujours ![]() .
.
![]()
Question 3
On se place dans un espace euclidien de dimension 3 de base orthonormale ![]() .
.
a) Les sous-espaces ![]() et
et ![]() sont des supplémentaires orthogonaux.
sont des supplémentaires orthogonaux.
b) Soit ![]() .
.
![]() est une projection orthogonale
est une projection orthogonale
Question 4
Soient ![]() et
et ![]() deux sous-espaces vectoriels de dimension finie du préhilbertien
deux sous-espaces vectoriels de dimension finie du préhilbertien ![]() .
.
On suppose que ![]()
![]() est une projection orthogonale.
est une projection orthogonale.
Question 5
Soient ![]() et
et ![]() deux sous-espaces vectoriels de dimension finie du préhilbertien
deux sous-espaces vectoriels de dimension finie du préhilbertien ![]() .
.
![]() ssi
ssi ![]() et
et ![]() sont stables par
sont stables par ![]() .
.
Question 6
On note ![]() l’ensemble des projections orthogonales définies sur l’espace euclidien
l’ensemble des projections orthogonales définies sur l’espace euclidien ![]() de dimension
de dimension ![]() .
.
![]() est une partie compacte de
est une partie compacte de ![]() .
.
3. Base orthonormale et distance à un plan.
On se place dans ![]() .
.
On considère le sous-espace vectoriel ![]() d’équations
d’équations ![]() et
et ![]() .
.
Question 1
![]() admet pour base
admet pour base ![]() avec
avec ![]() et
et ![]()
Question 2
Trouver une base orthonormale de ![]() .
.
Question 3
La distance de ![]() à
à ![]() est égale à
est égale à
a) ![]() b )
b ) ![]()
4. Caractérisation de supplémentaires orthogonaux en terme de distances.
Mines Ponts PC 2014.
Soient ![]() et
et ![]() deux sous-espaces vectoriels d’un espace euclidien
deux sous-espaces vectoriels d’un espace euclidien ![]() et on note
et on note ![]() la norme euclidienne associée.
la norme euclidienne associée.
Montrer que ![]() et
et ![]() sont des s.e.v. supplémentaires orthogonaux si, et seulement si, pour tout
sont des s.e.v. supplémentaires orthogonaux si, et seulement si, pour tout ![]() ,
, ![]() .
.
5. Endomorphisme 1-lipschitzien d’un espace euclidien
Mines Ponts MP
Soit ![]() un espace vectoriel euclidien et
un espace vectoriel euclidien et ![]() un endomorphisme de
un endomorphisme de ![]() tel que pour tout
tel que pour tout ![]() .
.
On définit ![]() tel que pour tout
tel que pour tout ![]() et
et ![]() dans
dans ![]() ,
, ![]() .
.
Question 1
a) Justifier l’existence de ![]() et montrer que
et montrer que ![]() est un endomorphisme de
est un endomorphisme de ![]() .
.
b) Pour tout ![]()
![]() .
.
Question 2
![]() .
.
Question 3
![]()
6. Matrice telle que 
CCP PSI 2006
Soit ![]() .
.
On suppose que ![]() .
.
On note ![]() (resp.
(resp. ![]() ) l’endomorphisme canoniquement associé à la matrice
) l’endomorphisme canoniquement associé à la matrice ![]() (resp.
(resp. ![]() ).
).
Question 1
Montrer que ![]()
En déduire que ![]() .
.
Question 2
![]() et
et ![]() ont les mêmes valeurs propres et les mêmes sous espaces propres.
ont les mêmes valeurs propres et les mêmes sous espaces propres.
Question 3
Soient ![]() et
et ![]() deux valeurs propres distinctes de
deux valeurs propres distinctes de ![]() . Les sous-espaces propres associés sont orthogonaux.
. Les sous-espaces propres associés sont orthogonaux.
Question 4
![]() .
.
Autres exercices sur les espaces euclidiens
Plan
1. Matrices blocs et matrices orthogonales (15mn)
2. Sur les coefficients d’une matrices orthogonale (35 mn)
3. Conservation de l’orthogonalité (25 mn)
4. Réflexions (40 mn)
5. Rotation en dimension 3 – exercice 1 (20 mn)
6. Rotation en dimension 3 – exercice 2 (25 mn) J’ai oublié de le supprimer. A ne pas faire, hp MP
7. Isométries de ![]() (30 mn)
(30 mn)
8. Endomorphismes antisymétriques et isométries (40 mn)
9. Matrices telles que ![]() (40 mn).
(40 mn).
1. Matrices blocs et matrices orthogonales
Soient ![]() ,
, ![]() ,
, ![]() ,
, ![]() et
et ![]() .
.
On suppose que ![]() et
et ![]() ou
ou ![]() .
.
Montrer que
![]() et
et ![]() .
.
2. Sur les coefficients d’une matrice orthogonale
Soit ![]() ,
, ![]() .
.
Question 1
Montrer que 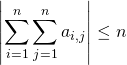 . Étudier le cas d’égalité.
. Étudier le cas d’égalité.
Question 2
a) 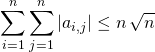 .
.
b) Cas d’égalité
Question 3
a) 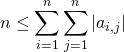 .
.
b) Cas d’égalité.
3. Conservation de l’orthogonalité
Question 1
Soit ![]() un endomorphisme non nul de l’espace vectoriel euclidien
un endomorphisme non nul de l’espace vectoriel euclidien ![]() .
.
![]() est une isométrie ssi deux vecteurs orthogonaux ont deux images par
est une isométrie ssi deux vecteurs orthogonaux ont deux images par ![]() orthogonales
orthogonales
Question 2
Si ![]() est un endomorphisme non nul de l’espace euclidien
est un endomorphisme non nul de l’espace euclidien ![]() tel que deux vecteurs orthogonaux ont deux images orthogonales, il existe
tel que deux vecteurs orthogonaux ont deux images orthogonales, il existe ![]() et une isométrie
et une isométrie ![]() tels que
tels que ![]() .
.
Question 3
Mines Ponts PC 2018
Déterminer l’ensemble des endomor- phismes ![]() non nuls de
non nuls de ![]() tels que pour tout sev
tels que pour tout sev ![]() de
de ![]() ,
, ![]() .
.
4. Réflexions
CCP MP 2017
Soit ![]() un espace euclidien de dimension
un espace euclidien de dimension ![]() .
.
Soit ![]() . On pose
. On pose ![]() .
.
On rappelle qu’une réflexion par rapport à l’hyperplan ![]() est la symétrie de
est la symétrie de ![]() sur
sur ![]() par rapport à
par rapport à ![]() .
.
Soit ![]() la réflexion par rapport à
la réflexion par rapport à ![]() et
et ![]() .
.
Question 1
![]() est une isométrie.
est une isométrie.
Question 2
![]() est une réflexion par rapport à
est une réflexion par rapport à
a) ![]() b)
b) ![]() c)
c) ![]() .
.
Question 3
![]() et
et ![]() commutent si, et seulement si,
commutent si, et seulement si, ![]() est vecteur propre de
est vecteur propre de ![]() .
.
Question 4 Première application de la question 3
Le centre de ![]() c’est à dire l’ensemble des
c’est à dire l’ensemble des ![]() tels que pour tout
tels que pour tout ![]() ,
, ![]() est égal à
est égal à ![]() .
.
Question 5 Deuxième application de la question 3
Soient ![]() et
et ![]() deux réflexions par rapport aux hyperplans
deux réflexions par rapport aux hyperplans ![]() et
et ![]() respectivement.
respectivement.
![]() et
et ![]() permutent ssi
permutent ssi ![]() ou
ou ![]() .
.
5- Rotation en dimension 3 – exercice 1
Soit ![]() une base orthonormale directe de
une base orthonormale directe de ![]() .
.
Démontrer qu’il existe une unique rotation ![]() telle que
telle que ![]() et si
et si ![]() ,
, ![]() .
.
Donner la matrice de ![]() dans la base
dans la base ![]() et en donner les éléments caractéris- tiques.
et en donner les éléments caractéris- tiques.
6. Isométries de 
On munit ![]() du produit scalaire canonique noté
du produit scalaire canonique noté ![]() .
.
Soit ![]() . On définit
. On définit ![]() et et
et et ![]() .
.
Question 1
Soit ![]() .
.
![]() et
et ![]() sont des isométries de
sont des isométries de ![]() .
.
Question 2
Si ![]() est une isométrie de
est une isométrie de ![]() , la matrice
, la matrice ![]() est-elle orthogonale ?
est-elle orthogonale ?
Question 3
Si ![]() est une isométrie de
est une isométrie de ![]() , la matrice
, la matrice ![]() est-elle orthogonale ?
est-elle orthogonale ?
7. Endomorphismes antisymétriques et isométries
Soient ![]() un espace euclidien et
un espace euclidien et ![]() un endomorphisme de
un endomorphisme de ![]() . On dit que
. On dit que ![]() est un endomorphisme antisiymétrique lorsque
est un endomorphisme antisiymétrique lorsque ![]() .
.
Question 1. Navale PSI
Si ![]() est un endomorphisme antisymétrique,
est un endomorphisme antisymétrique, ![]() .
.
Question 2
![]() un endomorphisme de
un endomorphisme de ![]() vérifie
vérifie ![]() ssi sa matrice dans une base orthonormale est antisymétrique.
ssi sa matrice dans une base orthonormale est antisymétrique.
Question 3
Si ![]() est un endomorphisme antisymétrique,
est un endomorphisme antisymétrique, ![]() .
.
Question 4
a) Si ![]() est un endomorphisme antisymétrique,
est un endomorphisme antisymétrique, ![]()
est défini et est une isométrie
b) L’endomorphisme ![]() ainsi défini est une rotation et n’admet pas
ainsi défini est une rotation et n’admet pas ![]() comme valeur propre.
comme valeur propre.
Question 5
Soit ![]() une isométrie n’admettant pas
une isométrie n’admettant pas ![]() pour valeur propre.
pour valeur propre.
Il existe un unique endomorphisme antisymétrique ![]() de
de ![]() tel que
tel que ![]() .
.
8. Matrices telles que 
MInes Ponts PSI 2015
Soient ![]() et
et ![]() deux matrices carrées d’ordre
deux matrices carrées d’ordre ![]() vérifiant
vérifiant ![]() .
.
Question 1
![]() .
.
Question 2
Soient ![]() et
et ![]() les endomorphismes canoniquement associés à
les endomorphismes canoniquement associés à ![]() et
et ![]() et
et ![]() .
.
![]() ,
, ![]() .
.
Question 3
Soit ![]() .
.
Il existe ![]() tel que
tel que ![]() soit une base de
soit une base de ![]() et
et ![]() soit une base de
soit une base de ![]() .
.
Question 4
Montrer qu’il existe ![]() , matrice orthogonale, telle que
, matrice orthogonale, telle que ![]() .
.
Annales sur les espaces euclidiens en maths spé
Retrouvez et entrainez-vous sur les annales de maths spé en mathématiques dans la rubrique Annales.
Profitez également de tous les autres cours en ligne de mathématiques et nos cours à domicile de maths au programme de Maths Spé, pour réviser régulièrement tout au long de l’année :

