Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Les Espaces Vectoriels MP, MPI, PC, PSI, PT
Résumé de cours Exercices et corrigés
Résumé de cours et méthodes – espaces vectoriels
1. Comment démontrer qu’un ensemble  est un
est un  -espace vectoriel ?
-espace vectoriel ?
![]() M1. On connaît un espace vectoriel
M1. On connaît un espace vectoriel ![]() tel que
tel que ![]() , il suffit de prouver que
, il suffit de prouver que ![]() est un sous-espace vectoriel de
est un sous-espace vectoriel de ![]() .
.
![]() M2. On ne peut trouver un tel espace vectoriel
M2. On ne peut trouver un tel espace vectoriel ![]() , il faut alors revenir à la définition d’un espace vectoriel et démontrer la structure de groupe commutatif pour l’addition et les 4 propriétés de la loi externe.
, il faut alors revenir à la définition d’un espace vectoriel et démontrer la structure de groupe commutatif pour l’addition et les 4 propriétés de la loi externe.
2. Comment utiliser le fait que  ?
?
![]() U1.
U1. ![]() est alors un sous-espace vectoriel : cela peut éviter beaucoup de calculs !
est alors un sous-espace vectoriel : cela peut éviter beaucoup de calculs !
![]() U2. Si l’on demande
U2. Si l’on demande ![]() , il suffit de chercher si
, il suffit de chercher si ![]() est une partie libre de
est une partie libre de ![]() .
.
![]() U3. Si l’on demande de prouver que
U3. Si l’on demande de prouver que ![]() est stable pour la multiplication (si
est stable pour la multiplication (si ![]() est une partie de
est une partie de ![]() , de
, de ![]() ou d’un ensemble de fonctions à valeurs dans
ou d’un ensemble de fonctions à valeurs dans ![]() ) ou pour la loi
) ou pour la loi ![]() (si
(si ![]() est une partie de
est une partie de ![]() ), il suffit de prouver que
), il suffit de prouver que
![]() et dans le cas de la loi
et dans le cas de la loi ![]()
![]() U4. Si l’on demande de prouver que
U4. Si l’on demande de prouver que ![]() est inclus dans le sous-espace vectoriel
est inclus dans le sous-espace vectoriel ![]() , il suffit de prouver que
, il suffit de prouver que ![]()
![]() U5. Si
U5. Si ![]() et si
et si ![]() , pour prouver que
, pour prouver que ![]() , il suffit de prouver que
, il suffit de prouver que ![]()
![]() .
.
3. Comment démontrer l’égalité de deux sous espaces vectoriels ?
![]() M1. Pour démontrer l’égalité des sous-espaces vectoriels
M1. Pour démontrer l’égalité des sous-espaces vectoriels ![]() et
et ![]() , on raisonne par double inclusion, en prouvant que
, on raisonne par double inclusion, en prouvant que ![]()
![]() M2. Si
M2. Si ![]() et
et ![]() sont de dimension finie et si l’on peut démontrer que
sont de dimension finie et si l’on peut démontrer que ![]() , il suffit de prouver une seule des deux inclusions.
, il suffit de prouver une seule des deux inclusions.
![]() M3. Lorsque
M3. Lorsque ![]() Vect
Vect![]() et
et ![]() est un sous-espace vectoriel, pour prouver que
est un sous-espace vectoriel, pour prouver que ![]() , il suffit de prouver que
, il suffit de prouver que ![]() et de dire que
et de dire que ![]() est le plus petit des sous-espaces vectoriels contenant
est le plus petit des sous-espaces vectoriels contenant ![]() .
.
PROF DE MATHS PARTICULIER
Des cours de qualité et enseignants aguerris
Préparer des concours ou s'exercer
Avis Google France ★★★★★ 4,9 sur 5
4. Comment démontrer qu’une famille est libre ?
![]() M1. Dans le cas d’une famille de deux vecteurs
M1. Dans le cas d’une famille de deux vecteurs ![]()
a) on démontre que ![]()
b) on démontre que la relation ![]() où
où ![]() est impossible.
est impossible.
![]() M2. Méthode générale pour démontrer que la famille
M2. Méthode générale pour démontrer que la famille ![]() est libre :
est libre :
on part de l’hypothèse: ![]() ,
, ![]() et on démontre que
et on démontre que ![]() .
.
![]() M3. On sait que
M3. On sait que ![]() est une famille libre et on veut prouver que
est une famille libre et on veut prouver que ![]() est encore une famille libre, on démontre que
est encore une famille libre, on démontre que ![]() n’est pas combinaison linéaire de
n’est pas combinaison linéaire de ![]()
Et quelques méthodes particulières :
![]() M4. On démontre que la famille
M4. On démontre que la famille ![]() est extraite d’une base connue.
est extraite d’une base connue.
![]() M5. On démontre que la famille
M5. On démontre que la famille ![]() est l’image d’une base par une application linéaire injective.
est l’image d’une base par une application linéaire injective.
![]() M6. Dans
M6. Dans ![]() , il suffit de prouver que l’on a une famille de polynômes de degrés 2 à 2 distincts.
, il suffit de prouver que l’on a une famille de polynômes de degrés 2 à 2 distincts.
![]() M7. Dans
M7. Dans ![]() , on peut regarder si la famille
, on peut regarder si la famille ![]() est une famille échelonnée, alors il s’agit d’une famille libre.
est une famille échelonnée, alors il s’agit d’une famille libre.
![]() M8. Pour démontrer que la famille infinie
M8. Pour démontrer que la famille infinie ![]() est libre, on démontre que toute sous-famille finie est libre.
est libre, on démontre que toute sous-famille finie est libre.
Dans le cas où ![]() , on démontre que pour tout
, on démontre que pour tout ![]() , la famille
, la famille ![]() est libre.
est libre.
Ce cours sur les espaces vectoriels est au programme de Maths de l’ensemble des filières de Maths Spé. Pour organiser un bon planning de révisions, prenez appui sur les nombreux cours en ligne de Maths en PT, les cours en ligne de Maths en MP, ou cours en ligne de PC en Maths, et cours en ligne de Maths en PSI, sans oublier nos profs particuliers de maths.
5. Comment démontrer qu’une famille est génératrice de  ?
?
Pour démontrer que ![]() est une famille génératrice de
est une famille génératrice de ![]() ,
,
![]() M1. Montrer que
M1. Montrer que
![]() Vect
Vect![]()
![]() M2. Montrer que pour tout
M2. Montrer que pour tout ![]() de
de ![]() , on peut trouver des scalaires
, on peut trouver des scalaires ![]() tels que
tels que
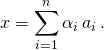
![]() M3. Si l’on connaît une base
M3. Si l’on connaît une base ![]() de
de ![]() , montrer que, pour tout
, montrer que, pour tout ![]() , on peut trouver
, on peut trouver ![]() de
de ![]() tel que
tel que 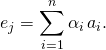 La famille
La famille ![]() engendre la base
engendre la base ![]() , c’est donc une famille génératrice de
, c’est donc une famille génératrice de ![]()
![]() M4. Pour démontrer que la famille infinie
M4. Pour démontrer que la famille infinie ![]() est génératrice de
est génératrice de ![]() , pour tout
, pour tout ![]() de
de ![]() , on démontre qu’il existe une famille presque nulle de scalaires
, on démontre qu’il existe une famille presque nulle de scalaires ![]() telle que
telle que ![]()
6 – Comment démontrer qu’une famille est une base de  ?
?
Soit ![]() . Penser à vérifier que les vecteurs de
. Penser à vérifier que les vecteurs de ![]() sont des éléments de
sont des éléments de ![]()
![]() M1. On connaît la dimension de
M1. On connaît la dimension de ![]() . On démontre
. On démontre
M1.1. que ![]() est une famille libre de
est une famille libre de ![]() et que
et que ![]()
ou M1.2. que ![]() est une famille génératrice de
est une famille génératrice de ![]() et que
et que ![]()
En général, M1.1. est plus simple que M1.2.
![]() M2. On ne connaît pas la dimension de
M2. On ne connaît pas la dimension de ![]() : on démontre que
: on démontre que ![]() est une famille génératrice et libre de
est une famille génératrice et libre de ![]()
Et quelques méthodes particulières:
![]() M3. Si l’on dispose de
M3. Si l’on dispose de ![]() polynômes de degrés 2 à 2 distincts de
polynômes de degrés 2 à 2 distincts de ![]() , ils forment une base de
, ils forment une base de
![]()
Si ![]() ,
, ![]() est un polynôme à coefficients dans
est un polynôme à coefficients dans ![]() de degré égal à
de degré égal à ![]() , la famille
, la famille ![]() est une base de
est une base de ![]() On dit que l’on a une famille de polynômes échelonnée en degrés.
On dit que l’on a une famille de polynômes échelonnée en degrés.
![]() M4. Si
M4. Si ![]() est un isomorphisme de
est un isomorphisme de ![]() sur
sur ![]() , l’image d’une base de
, l’image d’une base de ![]() par
par ![]() est une base de
est une base de ![]() .
.
![]() M5. Si
M5. Si ![]() et si pour tout
et si pour tout ![]() de
de ![]() ,
, ![]() est une base de
est une base de ![]() , la famille obtenue par juxtaposition des bases
, la famille obtenue par juxtaposition des bases ![]() est une base de
est une base de ![]() (dite adaptée à la décomposition en somme directe introduite).
(dite adaptée à la décomposition en somme directe introduite).
![]() M6. Si l’on sait que
M6. Si l’on sait que ![]() , on peut prouver que la matrice
, on peut prouver que la matrice ![]() de la famille de vecteurs
de la famille de vecteurs ![]() dans une base
dans une base ![]() de
de ![]() est inversible.
est inversible.
![]() M7. Si l’on sait que
M7. Si l’on sait que ![]() et si
et si ![]() est une base de
est une base de ![]() , on peut prouver que
, on peut prouver que ![]() .
.
![]() M8. Pour démontrer que la famille infinie
M8. Pour démontrer que la famille infinie ![]() est une base de
est une base de ![]() il faut prouver que c’est une partie libre et génératrice de
il faut prouver que c’est une partie libre et génératrice de ![]()
7. Comment prouver que  ?
?
S’assurer que ![]() et
et ![]() sont des sous-espaces vectoriels.
sont des sous-espaces vectoriels.
![]() M1. Cas général : on démontre que
M1. Cas général : on démontre que
a) ![]()
b) si ![]() et
et ![]() sont des sous-espaces vectoriels de
sont des sous-espaces vectoriels de ![]() , l’inclusion
, l’inclusion ![]() est évidente.
est évidente.
si ![]() et
et ![]() sont des sous-espaces vectoriels de
sont des sous-espaces vectoriels de ![]() et si
et si ![]() , il faut démontrer que
, il faut démontrer que ![]() .
.
c) pour tout ![]() de
de ![]() , on peut trouver
, on peut trouver ![]() et
et ![]() tels que
tels que ![]()
Pour cela :
M1.1. On a l’intuition de la décomposition : il suffit de vérifier que cette intuition est correcte.
M1.2. Sans intuition de la décomposition, on raisonne par analyse-synthèse.
analyse : En supposant que la décomposition ![]() existe, on détermine au moins l’un des éléments de cette décomposition en utilisant les propriétés de
existe, on détermine au moins l’un des éléments de cette décomposition en utilisant les propriétés de ![]() et
et ![]() , on en déduit le second élément en utilisant
, on en déduit le second élément en utilisant ![]()
synthèse : On introduit les vecteurs ![]() et
et ![]() obtenus par l’analyse, on vérifie que
obtenus par l’analyse, on vérifie que ![]() ,
, ![]() et
et ![]() .
.
![]() M2. On raisonne dans un espace vectoriel de dimension finie. Pour démontrer que les sous espaces vectoriels
M2. On raisonne dans un espace vectoriel de dimension finie. Pour démontrer que les sous espaces vectoriels ![]() et
et ![]() de
de ![]() sont supplémentaires dans
sont supplémentaires dans ![]() , il suffit d’utiliser l’une des deux méthodes suivantes :
, il suffit d’utiliser l’une des deux méthodes suivantes :
M2.1. On prouve que ![]() et que
et que ![]()
Cette méthode est bien adaptée à la démonstration de ![]() Im
Im ![]() Ker
Ker ![]() si
si ![]() lorsque
lorsque ![]() est un
est un ![]() -espace vectoriel de dimension finie puisque le théorème du rang assure que
-espace vectoriel de dimension finie puisque le théorème du rang assure que
dim Im ![]() + dim Ker
+ dim Ker ![]() = dim
= dim ![]()
M2.2. On prouve que ![]() et que
et que ![]()
![]() M3. Si
M3. Si ![]() est un
est un ![]() -espace vectoriel de dimension finie et si l’on a pu trouver une base
-espace vectoriel de dimension finie et si l’on a pu trouver une base ![]() de
de ![]() et une base
et une base ![]() de
de ![]() , il suffit de prouver que
, il suffit de prouver que
![]()
est une base de ![]() .
.
Ne vous arrêtez pas en si bon chemin, et travaillez les autres chapitres de Maths au programme de MP, MPI, PC et PSI avec les cours en ligne gratuits :
- réduction d’endomorphismes
- les matrices
- les espaces vectoriels normés
- les suites et séries de fonctions
- l’intégration sur un intervalle quelconque
Si vous souhaitez accéder à l’ensemble des méthodes et aux corrigés des exemples, n’hésitez pas à télécharger l’application PrepApp

