Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Les Espaces Vectoriels en MP, PC, MPI, PSI, PT
Résumé de cours Exercices et corrigés
Exercices et corrigés – espaces vectoriels
1. Famille libre
On note ![]() l’espace vectoriel des fonctions de
l’espace vectoriel des fonctions de ![]() dans
dans ![]() .
.
Si ![]() , on note
, on note ![]()
Montrer que la famille ![]() est libre.
est libre.
Corrigé de l’exercice :
Si ![]() , on note
, on note
![]() : la famille
: la famille ![]() est libre.
est libre.
![]() est vraie, car
est vraie, car ![]()
On suppose que ![]() est vraie.
est vraie.
Si l’on avait ![]() Vect
Vect![]() , il existerait des réels
, il existerait des réels ![]() tels que
tels que 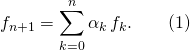
En dérivant deux fois la relation et en utilisant ![]() , on obtient :
, on obtient :
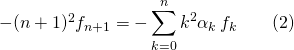
En formant ![]() , on obtient
, on obtient
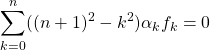 .
.
Par indépendance de la famille ![]() pour tout
pour tout ![]() ,
, ![]() donc
donc ![]() car
car ![]()
On en déduit que ![]() ce qui est absurde.
ce qui est absurde.
![]() n’est pas combinaison linéaire de la famille libre
n’est pas combinaison linéaire de la famille libre ![]() , donc
, donc ![]() est libre.
est libre.
On a prouvé ![]()
La propriété est démontrée par récurrence. On en déduit que la famille ![]() est libre.
est libre.
Quand le chapitre diagonalisation a été traité, la démonstration est plus simple.
On se place sur l’espace vectoriel ![]() des fonctions de classe
des fonctions de classe ![]() de
de ![]() dans
dans ![]() et on introduit l’endomorphisme
et on introduit l’endomorphisme ![]() de
de ![]() :
: ![]() .
.
Il suffit de remarquer que ![]() et
et ![]() .
.
On a donc introduit une famille de vecteurs propres de ![]() associés à des valeurs propres deux à deux distinctes. Elle est libre.
associés à des valeurs propres deux à deux distinctes. Elle est libre.
COURS DE MATHS
Nous avons recruté pour vous les meilleurs professeurs particuliers de maths
S'EXERCER ET APPRENDRE
Avis Google France ★★★★★ 4,8 sur 5
2. Endomorphisme et supplémentaires
Soit ![]() un espace vectoriel et
un espace vectoriel et ![]() un endomorphisme de
un endomorphisme de ![]() tel que
tel que ![]() et
et ![]() .
.
Question 1
Montrer que ![]() .
.
Question 2
![]()
Question 3
![]()
Corrigé de l’exercice :
1/ ![]() et
et ![]() sont des sous-espaces vectoriels de
sont des sous-espaces vectoriels de ![]() .
.
On raisonne par analyse-synthèse.
Analyse :
Soit ![]() . On suppose qu’il existe
. On suppose qu’il existe ![]() et
et ![]() tels que
tels que ![]() .
.
Alors ![]() et
et ![]() .
.
Donc ![]() .
.
Si la décomposition existe, elle est unique.
Synthèse :
On remarque que si ![]() ,
, ![]() donc
donc ![]() . (*)
. (*)
Si ![]() , on note
, on note ![]() et
et ![]() ;
; ![]()
![]() par (*)
par (*)
donc ![]()
et ![]() ,
,
donc ![]()
On a donc prouvé que ![]() .
.
La partie analyse a permis de prouver que la somme est directe.
Donc ![]() .
.
2/ Si l’on avait ![]() ,
,
pour tout ![]() , comme
, comme ![]() , on aurait
, on aurait ![]() , donc
, donc ![]() soit
soit ![]() ce qui contredit
ce qui contredit ![]() .
.
3/ ![]() Pour tout
Pour tout ![]() , il existe
, il existe ![]() tel que
tel que ![]() , alors
, alors ![]() , donc
, donc ![]() .
.
On a prouvé que ![]() .
.
![]() Si
Si ![]() ,
, ![]() , alors
, alors ![]() , donc
, donc ![]() .
.
On a prouvé que ![]() .
.
Par double inclusion, ![]() .
.
Parce qu’il n’est pas toujours facile de tout noter et tout comprendre directement pendant le cours dispensé en prépa, les cours en ligne de Maths en PC, ou les cours en ligne de Maths en PSI mais aussi les cours en ligne de Maths en MP, sont de bons moyens pour parfaire et compléter ses notes de cours et ses fiches de révisions.
3. Somme directe de  s.e.v.
s.e.v.
Exercice 1
Soit ![]() l’ensemble des fonctions de
l’ensemble des fonctions de ![]() dans
dans ![]() .
.
On note ![]() l’ensemble des fonctions constantes sur
l’ensemble des fonctions constantes sur ![]() ,
, ![]() l’ensemble des éléments de
l’ensemble des éléments de ![]() nuls sur
nuls sur ![]() et
et ![]() l’ensemble des éléments de
l’ensemble des éléments de ![]() nuls sur
nuls sur ![]()
Montrer que ![]()
Corrigé de l’exercice 1 :
On démontre facilement que ![]() ,
, ![]() et
et ![]() sont des sous-espaces vectoriels de
sont des sous-espaces vectoriels de ![]() .
.
On raisonne par analyse-synthèse.
Analyse : soit ![]() , on suppose que l’on peut écrire
, on suppose que l’on peut écrire ![]() avec
avec ![]()
![]() et
et ![]()
Il existe ![]() tel que
tel que ![]() et en prenant la valeur en 0,
et en prenant la valeur en 0, ![]()
Puis si ![]() ,
, ![]() car
car ![]() donc
donc ![]()
et si ![]()
![]() car
car ![]() donc
donc ![]()
On en déduit que si la décomposition existe, elle est unique.
Synthèse : Soit ![]()
On définit ![]() ,
,
![]()
et ![]()
Il est évident que ![]() ,
, ![]() et
et ![]() et que
et que ![]() (il suffit de distinguer les cas
(il suffit de distinguer les cas ![]() ,
, ![]() et
et ![]() ).
).
On a donc établi que ![]()
Exercice 2
Soient ![]() et
et ![]() deux projecteurs de
deux projecteurs de ![]() tels que
tels que ![]()
Montrer que ![]()
Corrigé de l’exercice 2 :
![]() ,
, ![]() et
et ![]() sont des sous-espaces vectoriels de
sont des sous-espaces vectoriels de ![]()
Analyse :
On suppose que ![]() avec
avec ![]()
![]() et
et ![]()
Comme ![]() et
et ![]() sont des projecteurs,
sont des projecteurs, ![]() et
et ![]()
![]()
![]() donc
donc ![]()
![]() donc
donc ![]()
Alors ![]()
Si la décomposition existe, elle est unique.
Synthèse :
Soit ![]() , on note
, on note ![]() ,
, ![]() et
et ![]()
![]()
![]() ,
,
![]() car
car ![]()
donc ![]()
![]()
![]()
![]() donc
donc ![]()
De plus ![]()
On avait justifié l’unicité de la décomposition dans la partie analyse.
On a donc prouvé que ![]()
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
4. Existence d’un endomorphisme
Exercice 1
Il existe une unique application linéaire ![]() sur
sur ![]() telle que si
telle que si ![]() est une matrice symétrique,
est une matrice symétrique, ![]() et si
et si ![]() est une matrice antisymétrique,
est une matrice antisymétrique, ![]()
Corrigé de l’exercice 1 :
En effet, ![]() où
où ![]() est le sous-espace vectoriel des matrices antisymétriques et
est le sous-espace vectoriel des matrices antisymétriques et ![]() est le sous-espace vectoriel des matrices symétriques.
est le sous-espace vectoriel des matrices symétriques.
L’application ![]()
![]() est linéaire
est linéaire
et l’application ![]()
![]() est linéaire.
est linéaire.
Par le théorème de recollement des applications linéaires, il existe donc un unique endomorphisme ![]() de
de ![]() tel que
tel que ![]() ,
, ![]() et
et ![]() ,
, ![]()
Exercice 2
On suppose que ![]() sont trois
sont trois ![]() -e.v. de dimension finie strictement positive.
-e.v. de dimension finie strictement positive.
Soit ![]() et
et ![]() .
.
Le but de l’exercice est de trouver une CNS pour que ![]() .
.
Question 1.
S’il existe ![]() tel que
tel que ![]() ,
, ![]() .
.
Question 2
On note ![]() ,
, ![]() et
et ![]() .
.
Dans les questions a) à e) on suppose que ![]() .
.
a) Il existe une base ![]() de
de ![]() telle que
telle que ![]() soit une base de
soit une base de ![]() .
.
b) On note si ![]() .
.
![]() est une base de
est une base de ![]() .
.
c) Il existe une base ![]() de
de ![]()
d) On définit ![]() tel que
tel que ![]() et
et ![]() si
si ![]() .
.
Si ![]() ,
, ![]() .
.
e) Si ![]() et si
et si ![]() , il existe
, il existe ![]() tel que
tel que ![]() .
.
Corrigé de l’exercice :
1/ Si ![]() ,
, ![]() donc
donc ![]() .
.
On a prouvé que ![]() .
.
2/ a/ ![]() est un sous-espace vectoriel de dimension
est un sous-espace vectoriel de dimension ![]() , on peut donc introduire une base de la forme
, on peut donc introduire une base de la forme ![]() .
.
C’est une famille libre de ![]() . Par le théorème de la base incomplète, on peut introduire une base de
. Par le théorème de la base incomplète, on peut introduire une base de ![]() de la forme
de la forme ![]() .
.
b/ Pour tout ![]() , il existe
, il existe ![]() tel que
tel que ![]() .
.
On écrit 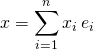 .
.
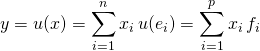 .
.
On a prouvé que ![]() est une famille génératrice de
est une famille génératrice de ![]() .
.
Elle est formée de ![]() vecteurs dans un espace vectoriel de dimension
vecteurs dans un espace vectoriel de dimension ![]() .
.
Donc ![]() est une base de
est une base de ![]()
c/ Comme ![]() ,
, ![]() est une famille libre de
est une famille libre de ![]() que l’on peut compléter en une base
que l’on peut compléter en une base ![]() de
de ![]() par le théorème de la base incomplète.
par le théorème de la base incomplète.
d/ L’application ![]() est bien définie par le théorème de caractérisation d’une application linéaire.
est bien définie par le théorème de caractérisation d’une application linéaire.
![]() ,
, ![]()
![]() ,
, ![]() .
.
Les applications linéaires ![]() et
et ![]() sont égales sur une base, donc
sont égales sur une base, donc ![]() .
.
e/ ![]() Si
Si ![]() ,
, ![]() est injective, l’image d’une base
est injective, l’image d’une base ![]() de
de ![]() par
par ![]() est une famille libre.
est une famille libre.
Donc en notant si ![]() ,
, ![]() est une famille libre de
est une famille libre de ![]() . On continue comme dans les questions d) et e).
. On continue comme dans les questions d) et e).
![]() Si
Si ![]() ,
, ![]() .
.
Comme ![]() , alors
, alors ![]() , donc
, donc ![]() et toute application linéaire
et toute application linéaire ![]() de
de ![]() dans
dans ![]() convient.
convient.
Conclusion : on a prouvé que ![]() ssi il existe
ssi il existe ![]() tel que
tel que ![]() .
.
5. Noyaux itérés
Question 1 Un résultat classique
a)Si ![]() où
où ![]() , il existe
, il existe ![]() tel que
tel que ![]() et si
et si ![]() ,
,
![]() .
.
b) L’entier ![]() étant défini dans la question a), montrer que si
étant défini dans la question a), montrer que si ![]() ,
, ![]() .
.
Question 2
Montrer que la suite ![]() est monotone pour l’inclusion et qu’elle est stationnaire à partir du même rang
est monotone pour l’inclusion et qu’elle est stationnaire à partir du même rang ![]() .
.
Question 3
Montrer que ![]() et que la restriction de
et que la restriction de ![]() à
à ![]() est un automorphisme de
est un automorphisme de ![]() .
.
Question 4 (plus difficile)
On note ![]() .
.
Montrer que ![]() .
.
Indication : introduire si ![]() , un supplémentaire
, un supplémentaire ![]() de
de ![]() dans
dans ![]() et montrer que
et montrer que ![]()
Corrigé de l’exercice :
1/ a/ Si ![]() ,
, ![]() donc
donc ![]() , alors
, alors ![]() , ce qui prouve que
, ce qui prouve que ![]() .
.
On a démontré que la suite ![]() est une suite croissante.
est une suite croissante.
![]() .
.
Il est impossible d’avoir : ![]()
![]() ,
,
car on aurait, puisque toutes les dimensions sont entières, ![]() , ce qui est absurde dans un espace vectoriel de dimension
, ce qui est absurde dans un espace vectoriel de dimension ![]()
On peut donc introduire ![]() le plus petit entier inférieur ou égal à
le plus petit entier inférieur ou égal à ![]() tel que
tel que ![]() , donc
, donc ![]()
et si ![]() ,
, ![]() .
.
b/ On peut alors établir par récurrence que si ![]() ,
, ![]()
La propriété est vraie pour ![]()
On suppose qu’elle est vraie au rang ![]() où
où ![]() est un entier supérieur ou égal à
est un entier supérieur ou égal à ![]()
Si ![]()
![]() ,
,![]() soit
soit ![]()
![]() soit
soit ![]()
Comme ![]() ,
, ![]() car
car ![]() , donc
, donc ![]()
L’inclusion contraire est évidente puisque la suite est croissante pour l’inclusion et ![]()
Par double inclusion, on a prouvé que ![]()
La propriété est vraie par récurrence sur ![]()
2/ Pour tout ![]() , si
, si ![]() , il existe
, il existe ![]() tel que
tel que ![]() avec
avec ![]() , donc
, donc ![]() , et alors
, et alors ![]() .
.
Donc la suite ![]() est une suite croissante.
est une suite croissante.
Si ![]() ,
,
![]()
![]()
![]()
donc ![]()
![]() .
.
Par la première question,
![]() si
si ![]() ,
, ![]() et alors
et alors ![]() .
.
![]() si
si ![]() ,
, ![]() , donc
, donc ![]() , on en déduit que si
, on en déduit que si ![]() ,
, ![]() .
.
On a montré que la suite ![]() est décroissante pour l’inclusion et est stationnaire à partir du même rang
est décroissante pour l’inclusion et est stationnaire à partir du même rang ![]() .
.
3/ Si ![]() , il existe
, il existe ![]() tel que
tel que ![]() et
et ![]() , donc
, donc ![]() ,
,
![]() , alors
, alors
![]() , donc
, donc ![]()
L’inclusion contraire étant toujours vraie, ![]() .
.
Comme de plus ![]() ,
,
on obtient ![]() .
.
Si ![]() ,
, ![]() et
et ![]() , donc, il existe
, donc, il existe ![]() tel que
tel que ![]() et
et ![]() ,
, ![]() ,
, ![]() .
.
L’endomorphisme ![]() du
du ![]() -espace vectoriel de dimension finie
-espace vectoriel de dimension finie ![]() est injectif. C’est donc un automorphisme.
est injectif. C’est donc un automorphisme.
La restriction de ![]() à
à ![]() est un automorphisme de
est un automorphisme de ![]() .
.
4/ On suppose que ![]() ,
, ![]() et les sous-espaces sont distincts.
et les sous-espaces sont distincts.
On introduit ![]() tel que
tel que ![]() . (*)
. (*)
![]() On démontre que
On démontre que ![]() .
.
![]() Si
Si ![]() , il existe
, il existe ![]() tel que
tel que ![]() , alors il existe
, alors il existe ![]() et
et ![]() tels que
tels que ![]() , donc
, donc ![]() avec
avec ![]() et
et ![]() ,
,
donc ![]() .
.
![]()
![]() et
et ![]() donc
donc ![]() .
.
On a montré que ![]() .
.
![]() On remarque que si
On remarque que si ![]() est un endomorphisme de
est un endomorphisme de ![]() , espace vectoriel de dimension finie, pour tout sev
, espace vectoriel de dimension finie, pour tout sev ![]() de
de ![]() différent de
différent de
![]() , l’image d’une base de
, l’image d’une base de ![]() est une partie génératrice de
est une partie génératrice de ![]() , donc
, donc ![]() , ce résultat reste vrai si
, ce résultat reste vrai si ![]() .
.
![]() On en déduit que
On en déduit que ![]()
donc ![]()
puis ![]()
ce qui donne ![]()
On termine avec ![]() par (*), soit
par (*), soit ![]() .
.
On a établi que :
![]() .
.
6. Hyperplan
Exercice 1
Question 1
Montrer que ![]() est un hyperplan de
est un hyperplan de ![]() et en déterminer une infinité de supplémentaires.
et en déterminer une infinité de supplémentaires.
Question 2
Déterminer une base de ![]()
Corrigé de l’exercice 1 :
1/ Soit ![]()
![]() ,
, ![]() est une forme linéaire (démonstration simple) non nulle (car
est une forme linéaire (démonstration simple) non nulle (car ![]() ).
).
Comme ![]()
![]() est un hyperplan de
est un hyperplan de ![]()
Pour tout ![]() ,
, ![]() , donc
, donc ![]() est un supplémentaire de
est un supplémentaire de ![]()
2/ ![]()
![]() il existe
il existe ![]() [X] tel que
[X] tel que ![]()
![]() il existe une suite
il existe une suite ![]() de scalaires nuls à partir d’un certain rang telle que
de scalaires nuls à partir d’un certain rang telle que 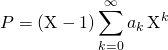
soit 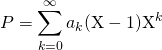 . On a prouvé que la famille
. On a prouvé que la famille ![]() est une famille génératrice de
est une famille génératrice de ![]() .
.
C’est une famille libre car formée de polynômes de degrés deux à deux distincts, donc c’est une base de ![]()
L’année de Maths Spé, est l’année des concours, par conséquent, tous les étudiants de Maths Spé, doivent s’assurer de leur niveau de connaissances avant de se lancer dans les grands entrainements sur les annales. N’hésitez pas à faire appel à un prof de maths à domicile pour bien progresser et viser les meilleurs concours. Ainsi, pour s’assurer de leurs connaissances, voici quelques cours qu’il est important de revoir :
- réduction d’endomorphismes
- les matrices
- les espaces vectoriels normés
- les suites et séries de fonctions
- l’intégration sur un intervalle quelconque
Pour avoir les corrigés de tous les exercices et accéder à tous les exercices et annales corrigés, n’hésitez pas à télécharger l’application mobile PrepApp.

