Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Intégration sur un intervalle quelconque en Maths Spé
Résumé de cours Exercices et corrigés
Exercices et corrigés sur Intégration sur un intervalle quelconque
1. Convergence d’intégrales
Exercice 1
Montrer que ![]() est intégrable sur
est intégrable sur ![]()
Corrigé de l’exercice 1 :
On utilise
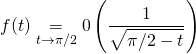 .
.La fonction
Exercice 2
Étude de l’intégrabilité selon le réel ![]() de
de ![]() sur
sur ![]() .
.
Corrigé de l’exercice 2 :
![]() est continue sur
est continue sur ![]() . Au voisinage de
. Au voisinage de ![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]() si
si ![]() ,
, ![]()
donc ![]() est du signe de
est du signe de ![]() au voisinage de
au voisinage de ![]() et comme
et comme ![]() n’est pas intégrable sur
n’est pas intégrable sur ![]() ,
, ![]() n’est pas intégrable sur
n’est pas intégrable sur ![]() .
.
![]() si
si ![]() ,
, ![]() donc par comparaison par équivalence,
donc par comparaison par équivalence, ![]() est intégrable sur
est intégrable sur ![]() , donc
, donc ![]() est intégrable sur
est intégrable sur ![]() .
.
Exercice 3
Montrer que ![]() est intégrable sur
est intégrable sur ![]() ssi
ssi ![]()
Corrigé de l’exercice 3 :
![]() est continue sur
est continue sur ![]() .
.
![]() Si
Si ![]() , soit
, soit ![]() ,
, ![]() car
car ![]() donc
donc ![]() . La fonction
. La fonction ![]() est intégrable sur
est intégrable sur ![]() , donc, par domination,
, donc, par domination, ![]() est intégrable sur
est intégrable sur ![]() .
.
![]() Si
Si ![]() , pour
, pour ![]() et
et ![]() ; par minoration par une fonction non intégrable sur
; par minoration par une fonction non intégrable sur ![]() ,
, ![]() n’est pas intégrable sur
n’est pas intégrable sur ![]() .
.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
2. D’autres convergences et aussi des calculs d’intégrales
Exercice 4
Convergence de ![]() .
.
Corrigé de l’exercice 4 :
![]() La fonction
La fonction ![]() :
: ![]() et
et ![]() est continue sur
est continue sur ![]() .
.
Si ![]() , si
, si ![]() .
.
Donc pour tout ![]() , alors
, alors ![]() est définie.
est définie.
La fonction ![]() est continue sur
est continue sur ![]() .
.
![]() En utilisant le développement limité de
En utilisant le développement limité de ![]() à l′ordre 2 au voisinage de
à l′ordre 2 au voisinage de ![]() (
(![]() tend vers
tend vers ![]() en
en ![]() ),
),
![]()
On a donc écrit ![]() avec
avec ![]()
![]() .
.
On sait (exercice classique) que l’intégrale ![]() converge.
converge.
Comme ![]() ,
, ![]() est intégrable sur
est intégrable sur ![]() , alors
, alors ![]() l’est aussi, donc l’intégrale
l’est aussi, donc l’intégrale ![]() converge.
converge.
On en déduit par différence de deux intégrales convergentes que l’intégrale ![]() converge.
converge.
Donc l’intégrale ![]() converge.
converge.
Exercice 5
Convergence et calcul de ![]() .
.
Corrigé de l’exercice 5 :
![]() Soit
Soit ![]() ,
, ![]() est continue sur
est continue sur ![]() .
.
![]()
![]() ,
, ![]() est intégrable sur
est intégrable sur ![]() , donc
, donc ![]() est intégrable sur
est intégrable sur ![]() par comparaison par équivalence de fonctions à valeurs négatives ou nulles.
par comparaison par équivalence de fonctions à valeurs négatives ou nulles.
![]()
![]() , comme
, comme ![]() admet 0 pour limite en 1, on prolonge
admet 0 pour limite en 1, on prolonge ![]() par continuité en 1 en posant
par continuité en 1 en posant ![]() et
et ![]() est intégrable sur
est intégrable sur ![]() comme fonction continue.
comme fonction continue.
On a prouvé que ![]() est intégrable sur
est intégrable sur ![]() .
.
![]() La fonction
La fonction
![]() ,
, ![]()
est une bijection strictement décroissante et de classe ![]() et la fonction
et la fonction ![]() est intégrable sur
est intégrable sur ![]() . Par le théorème de changement de variable,
. Par le théorème de changement de variable,
![]()
![]()
![]()
en utilisant ![]()
et ![]() est une primitive de
est une primitive de ![]() ,
,
donc ![]() est une primitive sur
est une primitive sur ![]() de
de ![]()
et ![]() est une primitive sur
est une primitive sur ![]() de
de ![]()
![]()
![]()
donc ![]()
car ![]() .
.
Exercice 6
Convergence et valeur de ![]() .
.
Corrigé de l’exercice 6 :
La fonction ![]() est continue, positive et paire.
est continue, positive et paire.
![]() , donc par comparaison par équivalence à une fonction intégrable sur
, donc par comparaison par équivalence à une fonction intégrable sur ![]() ,
, ![]() l’est aussi.
l’est aussi.
Par parité, ![]() est intégrable sur
est intégrable sur ![]() .
.
![]()
donc ![]() .
.
On doit donc calculer ![]() .
.
La fonction ![]() définit une bijection de
définit une bijection de ![]() sur
sur ![]() de classe
de classe ![]() strictement croissante et la fonction
strictement croissante et la fonction
continue ![]() est intégrable sur
est intégrable sur ![]() .
.
On remarque que
![]()
On applique le théorème de changement de variable,
![]() .
.
donc ![Rendered by QuickLaTeX.com \displaystyle \int_{- \infty}^{+\infty} \frac {\textrm{ch} (t) } {\textrm{ch} (2t) }\, \textrm{d} \, t = \left [ \frac { \textrm {Arctan} \left (\sqrt {2} \; u \right )} {\sqrt{2}} \right] _ { - \infty} ^{+ \infty}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-e564c1bc9e7185b8f9ae609d006e4b6f_l3.png)
![]() .
.
Enrichissez vos fiches de révisions avec les cours en ligne de Maths en MP, les cours en ligne de Maths en PSI mais aussi les cours en ligne de Maths de PC.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
3. Comparaison d’une intégrale avec une série
Exercice 7
Si ![]() est continue par morceaux sur
est continue par morceaux sur ![]() décroissante et à valeurs positives ou nulles, lorsque
décroissante et à valeurs positives ou nulles, lorsque ![]() est intégrable sur
est intégrable sur ![]() encadrer à l’aide de deux intégrales
encadrer à l’aide de deux intégrales 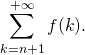
Corrigé de l’exercice 7 :
En intégrant sur
Donc si
puis en sommant si
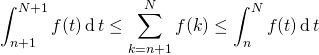 .
.On peut passer à la limite lorsque
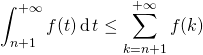
Lorsque ![]() , une division par
, une division par ![]() de l’encadrement précédent permet de dire que le reste
de l’encadrement précédent permet de dire que le reste ![]() est équivalent à
est équivalent à ![]() .
.
C’est le cas par exemple pour ![]() pour
pour ![]() .
.
Exercice 8 MinesPonts PSI 2017.
Soit ![]() une fonction de classe
une fonction de classe ![]() de
de ![]() dans
dans ![]() .
.
Question 1
Montrer que pour tout ![]()
![]()
![]() .
.
Question 2
On suppose que ![]() est intégrable sur
est intégrable sur ![]() .
.
Montrer que la série ![]() converge si, et seulement si, la série de terme général
converge si, et seulement si, la série de terme général ![]() converge.
converge.
Question 3
Montrer que la série ![]() et l’intégrale
et l’intégrale ![]() sont de même nature.
sont de même nature.
Conclure.
Corrigé de l’exercice 8 :
Question 1 :
Par intégration par parties en utilisant les fonctions ![]() et
et ![]() qui sont de classe
qui sont de classe ![]() sur
sur ![]() ,
,
![]()
![]()
soit ![]()
![]() .
.
Question 2 :
La série de terme général ![]() vérifie
vérifie ![]() donc est absolument convergente car pour tout
donc est absolument convergente car pour tout ![]() , les sommes partielles de la série à termes positifs
, les sommes partielles de la série à termes positifs ![]() sont majorées par
sont majorées par ![]() .
.
En écrivant que ![]() , on en déduit que
, on en déduit que ![]() converge ssi
converge ssi ![]() converge.
converge.
Question 3 :
donc
On peut donc utiliser la question a).
On en déduit que
On note
Comme l’intégrale diverge, la série est divergente.
4. Fonctions définies par une intégrale
Exercice 9 Mines Ponts 2017 MP
Soit ![]() .
.
Question 1
Justifier l’existence de ![]() pour tout réel
pour tout réel ![]() , trouver sa limite en
, trouver sa limite en ![]() , sa dérivée, un équivalent en
, sa dérivée, un équivalent en ![]() .
.
Question 2
Montrer que ![]() est intégrable sur
est intégrable sur ![]() et calculer son intégrale.
et calculer son intégrale.
Corrigé de l’exercice 9 :
Question 1 :
La fonction ![]() est continue sur
est continue sur ![]() et vérifie
et vérifie ![]() ,
,
donc ![]() est intégrable sur
est intégrable sur ![]() , et alors
, et alors ![]() est intégrable sur
est intégrable sur ![]() pour tout réel
pour tout réel ![]() .
.
En écrivant ![]() , on obtient :
, on obtient : ![]() est de classe
est de classe ![]() sur
sur ![]() et
et ![]() .
.
En utilisant cette relation, ![]() admet
admet ![]() pour limite en
pour limite en ![]() .
.
On écrit si ![]() ,
, ![]()
Les fonctions ![]() et
et ![]() sont de classe
sont de classe ![]() sur
sur ![]() ,
, ![]() admet
admet ![]() pour limite en
pour limite en ![]() et
et ![]() pour limite en
pour limite en ![]() , par le théorème d’intégration par parties,
, par le théorème d’intégration par parties,
![]() .
.
![]()
Si ![]() ,
,
![]()
![]()
![]()
donc ![]()
puis ![]()
et ![]() .
.
Question 2 :
La fonction ![]() est continue et équivalente en
est continue et équivalente en ![]() à une fonction intégrable car
à une fonction intégrable car ![]() .
.
Par intégration par parties, les fonctions ![]() et
et ![]() étant de classe
étant de classe ![]() , la fonction
, la fonction ![]() est intégrable sur
est intégrable sur ![]() ,
, ![]() et
et ![]() , en utilisant l’ équivalent de
, en utilisant l’ équivalent de ![]() obtenu en b),
obtenu en b),
![]()
![]() .
.
Soyez sûrs de vous et de vos connaissances en Maths avec les cours en ligne et les exercices corrigés des chapitres de maths au programme de Maths Spé :
- les séries entières
- le dénombrement
- les intégrales à paramètre
- les variables aléatoires
- les probabilités
Pour avoir les corrigés de tous ces exercices et accéder à tous les exercices et annales corrigés, n’hésitez pas à télécharger l’application mobile PrepApp.

