Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Exercices Matrices en Maths Spé
Résumé de cours Exercices et corrigés
Ces exercices sur les matrices en prepa maths spé reprennent certaines notions déjà vues en maths sup. Ces exercices sont classiques et pour certains incontournables pour la réussite sur la partie algèbre linéaire aux concours. Pour travailler de manière plus ciblée, n’hésitez pas à demander une mise en contact pour un cours de maths à domicile avec un des professeurs de la plateforme Groupe Réussite.
Matrices en MP, PC, MPI, PSI et PT (inverse d’une matrice, noyau & image)
1. Calcul d’une matrice  en prepa maths spé
en prepa maths spé
Exercice 1
Soit 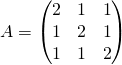 .
.
Exprimer ![]() en fonction de
en fonction de ![]() et
et ![]() .
.
En déduire la valeur de ![]() si
si ![]()
Corrigé de l’exercice 1 :
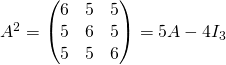
Soit ![]()
![]()
Par le théorème de division euclidienne, il existe ![]() et deux réels
et deux réels ![]() et
et ![]() tels que
tels que
![]() .
.
En prenant la valeur en 1 et en 4, on obtient :
![]() et
et ![]()
![]() et
et ![]()
Donc ![]()
![]() .
.
Exercice 2
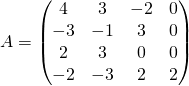
Vérifier que si ![]()
![]()
En déduire la valeur de ![]() si
si ![]() .
.
Corrigé de l’exercice 2 :
Vous avez vérifié par calcul que ![]() et remarqué que
et remarqué que
![]() .
.
Il existe ![]() tel que
tel que ![]() où
où ![]() est de degré inférieur ou égal à 2.
est de degré inférieur ou égal à 2.
Il existe ![]() tel que
tel que ![]() .
.
On écrit que ![]() est divisible par
est divisible par ![]()
![]()
![]()
![]()
et ![]()
On obtient un système de trois équations à trois inconnues permettant de déterminer ![]() ,
, ![]() ,
, ![]() :
:
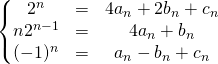
![]()
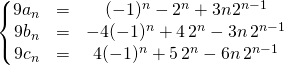
Puis ![]()
Exercice 3
Si 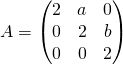 , calculer
, calculer ![]() pour
pour ![]()
Corrigé de l’exercice 3 :
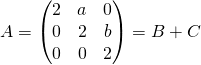
avec ![]() et
et 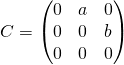 ,
,
![]() ,
, 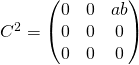
et ![]() .
.
Par le binôme de Newton :
![]() ,
,
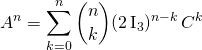
![]()
![]()
![]()
(on vous laisse finir le calcul).
PROF DE MATHS PARTICULIER
Des cours de qualité et enseignants aguerris
Préparer des concours ou s'exercer
Avis Google France ★★★★★ 4,9 sur 5
2. Calcul de l’inverse d’une matrice maths spé
Exercice 1
Calculer l’inverse de la matrice
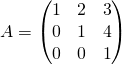
en introduisant une matrice nilpotente.
Corrigé de l’exercice 1 :
![]() où
où
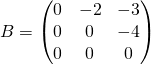 .
.
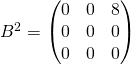 et
et ![]()
Comme ![]() ,
, ![]() .
.
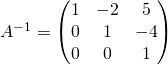 .
.
Exercice 2
On rappelle que si 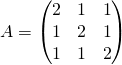 ,
,
![]() .
.
Montrer que ![]() est inversible et calculer
est inversible et calculer ![]() .
.
Corrigé sur l’exercice 2 :
![]() donc
donc
![]() .
.
![]() est inversible et
est inversible et
![]()
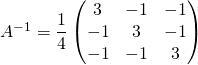 .
.
Exercice 3
Montrer que 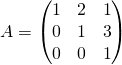
est une matrice inversible et calculer son inverse en l’interprétant comme une matrice de changement de bases.
Corrigé de l’exercice 3 :
![]() est inversible puisque
est inversible puisque ![]()
Si ![]() est la matrice de passage de la base
est la matrice de passage de la base ![]() à la base
à la base ![]()
![]() ,
, ![]() et
et ![]() ,
,
donc ![]() ,
, ![]() et
et ![]()
![]() est la matrice de passage de la base
est la matrice de passage de la base ![]() à la base
à la base ![]() donc
donc
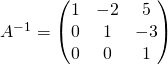 .
.
3. Noyau et image de  défini par sa matrice en MP, MPI, PC, PSI, PT
défini par sa matrice en MP, MPI, PC, PSI, PT
Exercice 1
Déterminer simultanément le rang de ![]() , une base de
, une base de ![]() et de
et de ![]() si la matrice de
si la matrice de ![]() dans les bases
dans les bases ![]() de
de ![]() et
et ![]() de
de ![]() est égale à
est égale à 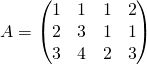 .
.
Corrigé de l’exercice 1 :
Soit ![]() de matrice
de matrice ![]() dans les bases
dans les bases ![]() de
de ![]() et
et ![]() de
de ![]() .
.
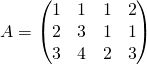 .
.
On effectue les opérations
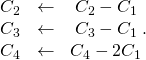
pour obtenir :
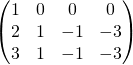
puis avec
puis ![]() ,
,
on obtient :
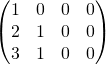
On a donc obtenu avec les opérations ci-dessus :
![]()
![]()
![]()
![]()
![]() .
.
où ![]()
![]() .
.
Les vecteurs ![]() et
et ![]() forment une famille libre de
forment une famille libre de ![]() espace vectoriel de dimension 2 , ils forment donc une base de
espace vectoriel de dimension 2 , ils forment donc une base de ![]() .
.
Les vecteurs ![]() ,
, ![]() sont dans Ker
sont dans Ker ![]() et ne sont pas colinéaires.
et ne sont pas colinéaires.
Ils forment donc une base de Ker ![]() puisque, par le théorème du rang,
puisque, par le théorème du rang,
![]()
Exercice 2
Déterminer une base de Ker ![]() si la matrice de
si la matrice de ![]() dans les bases
dans les bases ![]() de
de ![]() et
et ![]() de
de ![]() est égale à
est égale à 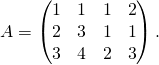
Corrigé de l’exercice 2 :
C’est la même matrice que dans l’exercice précédent mais on cherche seulement le noyau.
![]()
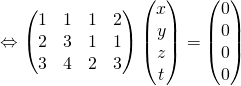
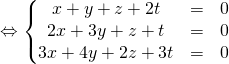
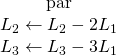
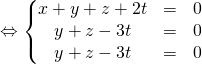
![]()
Donc
![]()
![]()
Soit ![]() et
et ![]() .
.
![]() .
.
![]() et
et ![]() ne sont pas colinéaires et
ne sont pas colinéaires et ![]() , donc
, donc ![]() est une base de Ker
est une base de Ker ![]() .
.
Exercice 3
Déterminer une base de Im ![]() si la matrice de
si la matrice de ![]() dans les bases
dans les bases ![]() de
de ![]() et
et ![]() de
de ![]() est égale à
est égale à 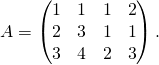
Corrigé de l’exercice 3 :
On utilise toujours la matrice des deux exercices précédents mais on ne cherche que l’image dans cet exercice.
En effectuant les opérations
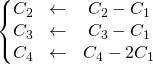 ,
,
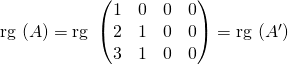 .
.
![]()
![]()
![]()
![]()
![]()
car les deux premières colonnes de ![]() forment une famille libre et les deux dernières colonnes sont nulles.
forment une famille libre et les deux dernières colonnes sont nulles.
Les vecteurs ![]() et
et ![]() , soit
, soit ![]() et
et ![]() , forment une base de Im
, forment une base de Im ![]() .
.
Les matrices sont un chapitre important en Maths Spé, un cours déjà vu en Maths Sup qui est davantage complexifié en Maths Spé. De nombreux cours de Maths Spé suivent cette même logique. C’est pourquoi des cours en ligne de Maths en MP, mais aussi des cours en ligne de Maths en PC et également des cours en ligne de Maths en PSI sont mis à disposition des étudiants pour les aider à réussir leur dernière année de prépa.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
4. Utilisation de la base canonique
Exercice 1
Déterminer l’ensemble des matrices ![]() telles que pour tout
telles que pour tout ![]() de
de ![]() ,
, ![]()
Corrigé de l’exercice 1 :
On raisonne par analyse-synthèse.
Analyse : on suppose que ![]() est telle que pour tout
est telle que pour tout ![]() de
de ![]() ,
, ![]()
Si ![]() , en refaisant les calculs du §4 des méthodes , on démontre que pour tout
, en refaisant les calculs du §4 des méthodes , on démontre que pour tout ![]() ,
,
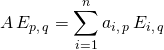
et 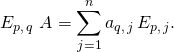
On sait que ![]() .
.
Si ![]() en comparant les coefficients de
en comparant les coefficients de ![]() , on obtient
, on obtient ![]() ,
,
et en comparant ceux de ![]() , on obtient
, on obtient ![]() .
.
On a donc démontré qu’il existe ![]() tel que
tel que ![]() .
.
Synthèse : S’il existe ![]() tel que
tel que ![]() , il est évident que pour tout
, il est évident que pour tout ![]() de
de ![]() ,
, ![]()
Conclusion : L’ensemble des matrices ![]() qui permutent avec tout
qui permutent avec tout ![]() de
de ![]() est égal à Vect
est égal à Vect![]()
Exercice 2
Démontrer que pour toute application linéaire ![]() de
de ![]() dans
dans ![]() il existe une unique matrice
il existe une unique matrice ![]() telle que
telle que
![]() ,
, ![]() .
.
Corrigé de l’exercice 2 :
On raisonne par analyse-synthèse.
Soit ![]() une application linéaire
une application linéaire ![]() de
de ![]() dans
dans ![]()
Analyse : On suppose qu’il existe ![]() telle que
telle que
![]() ,
, ![]()
On note ![]() . En refaisant les calculs du § 4 des méthodes, on démontre que pour tout
. En refaisant les calculs du § 4 des méthodes, on démontre que pour tout ![]() ,
, 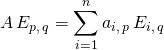
donc ![]()
Le problème a donc au plus une solution ![]() telle que
telle que
si ![]() ,
, ![]()
Synthèse :
On définit la matrice ![]() par
par ![]()
où ![]()
Grâce au calcul de la partie analyse,
![]() ,
, ![]()
On démontre facilement que l’application ![]() est linéaire.
est linéaire.
Les applications linéaires ![]() et
et ![]() sont égales sur la base canonique de
sont égales sur la base canonique de ![]() elles sont donc égales.
elles sont donc égales.
Conclusion : pour toute application linéaire ![]() de
de ![]() dans
dans ![]() , il existe une unique matrice
, il existe une unique matrice ![]() telle que
telle que
![]() ,
, ![]()
5. Détermination de suites
Déterminer les suites ![]() ,
, ![]() ,
, ![]() définies par les termes initiaux
définies par les termes initiaux ![]()
![]() et
et ![]() et les relations
et les relations
![]()
![]() ,
, ![]()
et ![]() .
.
Corrigé de l’exercice :
Si ![]() ,
, ![]() et
et ![]() , en posant
, en posant
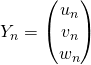 et
et 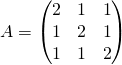 ,
,
![]() , donc
, donc ![]()
avec 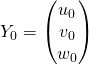 .
.
On a vu dans l’exercice 1 du ![]() que
que
![]() ,
,
donc ![]() .
.
En effectuant les calculs, on obtient pour tout ![]() ,
,
![]()
![]()
![]()
6. Matrices semblables
Exercice 1
Que pouvez vous dire d’une matrice semblable à ![]() ?
?
Corrigé de l’exercice 1 :
Si ![]() est semblable à
est semblable à ![]() , il existe
, il existe ![]() telle que
telle que
![]()
donc ![]() .
.
La réciproque est évidente, car toute matrice est semblable à elle-même.
Exercice 2
Soient ![]() et
et ![]() deux matrices carrées d’ordre
deux matrices carrées d’ordre ![]() telles que
telles que ![]() et
et ![]() . Si
. Si ![]() et
et ![]() ont même trace ?
ont même trace ?
Corrigé de l’exercice 2 :
L’affirmation est vraie, mais doit être justifiée.
L’endomorphisme ![]() canoniquement associé à
canoniquement associé à ![]() vérifie
vérifie ![]() , donc est un projecteur.
, donc est un projecteur.
En notant ![]() et en utilisant une base adaptée à la somme directe
et en utilisant une base adaptée à la somme directe ![]() , la matrice
, la matrice ![]() est semblable à
est semblable à ![]()
et ![]()
Comme ![]() vérifie les mêmes conditions que
vérifie les mêmes conditions que ![]() ,
, ![]() est aussi semblable à
est aussi semblable à ![]() et alors
et alors ![]() et
et ![]() sont semblables, puisque la relation « être semblable » est une relation d’équivalence sur l’ensemble
sont semblables, puisque la relation « être semblable » est une relation d’équivalence sur l’ensemble ![]()
Exercice 4
Si ![]() est carrée d’ordre 3, non nulle et vérifie
est carrée d’ordre 3, non nulle et vérifie ![]() , comment démontrer que
, comment démontrer que ![]() est semblable à
est semblable à 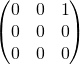 ?
?
Corrigé de l’exercice 3 :
On note ![]() et
et ![]() l’endomorphisme canoniquement associé à
l’endomorphisme canoniquement associé à ![]() ,
,
![]() vérifie
vérifie ![]() et
et ![]()
Pour tout ![]() , il existe
, il existe ![]() tel que
tel que ![]() , donc
, donc ![]() soit
soit ![]() , on a donc prouvé que
, on a donc prouvé que ![]() .
.
D’autre part ![]() car
car ![]() .
.
On en déduit que
![]()
et par le théorème du rang,
![]() ,
,
donc ![]() et
et ![]()
On cherche donc dans la suite une base ![]() de
de ![]() telle que
telle que
![]() et
et ![]() .
.
Soit ![]() une base de
une base de ![]() , il existe donc
, il existe donc ![]() tel que
tel que ![]() , puis
, puis ![]()
![]() est un vecteur non nul de Ker
est un vecteur non nul de Ker ![]() , espace vectoriel de dimension 2, il existe donc une base
, espace vectoriel de dimension 2, il existe donc une base ![]() de Ker
de Ker ![]()
![]() , alors
, alors ![]() est une base de
est une base de ![]() dans laquelle la matrice de
dans laquelle la matrice de ![]() est la matrice
est la matrice 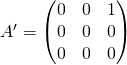
![]() et
et ![]() sont semblables.
sont semblables.
Les concours de Maths Spé sont réputés pour leur difficulté, notamment car, il est fondamental pour tous les étudiants de connaître parfaitement l’ensemble des cours au programme de Maths Spé. Alors, pour s’assurer d’avoir un bon niveau, voici quelques chapitres à réviser :
- les espaces vectoriels normés
- les suites et séries de fonctions
- l’intégration sur un intervalle quelconque
- les séries entières
- le dénombrement
Pour avoir les corrigés de tous ces exercices et accéder à tous les exercices et annales corrigés, n’hésitez pas à télécharger l’application mobile PrepApp.

