Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Réduction des endomorphismes MP, MPI, PC, PSI et PT
Résumé de cours Exercices et corrigés
Exercices et corrigés – Réduction des endomorphismes
1. Des exemples pratiques de diagonalisation
Exercice 1
Soit 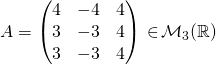 .
.
Est-elle diagonalisable ? Si oui, la diagonaliser.
Corrigé de l’exercice 1 :
![]() Si
Si ![]() ,
, 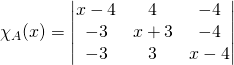
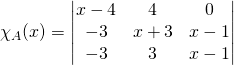
par ![]()
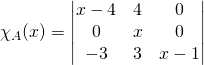
par ![]()
Si ![]()
![]() .
. ![]() est diagonalisable.
est diagonalisable.
![]()
![]()
![]()
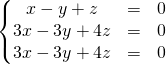
![]()
![]() avec
avec 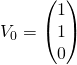 .
.
![]()
![]()
![]()
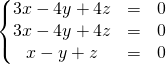
![]()
![]() avec
avec 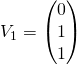 .
.
![]()
![]()
![]()
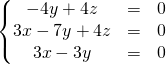
![]()
![]()
![]() avec
avec 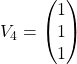 .
.
![]() On peut écrire :
On peut écrire : ![]() où
où
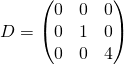 et
et 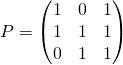 .
.
Exercice 2
Soit 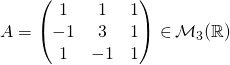 .
.
Est-elle diagonalisable ? Si oui, la diagonaliser.
Corrigé de l’exercice 2 :
![]() On calcule le polynôme caractéristique
On calcule le polynôme caractéristique
Si ![]() ,
, 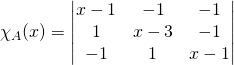
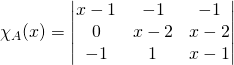
par ![]()
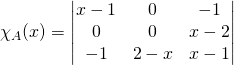
par ![]()
Si ![]()
![]() .
.
![]() est diagonalisable ssi
est diagonalisable ssi ![]() .
.
![]() On détermine le sous-espace propre associé à la valeur propre 2 :
On détermine le sous-espace propre associé à la valeur propre 2 :
![]()
![]()
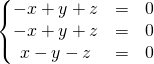
![]()
Il est de dimension 2, donc ![]() est diagonalisable.
est diagonalisable.
![]()
avec 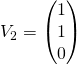 et
et 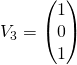 .
.
![]() On détermine le sous-espace propre associé à la valeur propre 1 :
On détermine le sous-espace propre associé à la valeur propre 1 :
![]()
![]()
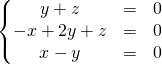
![]() .
.
![]() avec
avec 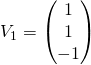
![]() On a déjà précisé que
On a déjà précisé que ![]() est diagonalisable.
est diagonalisable.
On peut écrire : ![]() où
où
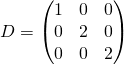 et
et 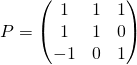 .
.
Exercice 3
Soit ![]() et
et ![]() avec
avec ![]() si
si ![]() et
et ![]() sinon.
sinon.
Réduire la matrice ![]() .
.
Corrigé de l’exercice 3 :
La matrice ![]() est carrée d’ordre
est carrée d’ordre ![]() , formée de 1 en dernière ligne et dernière colonne, les autres termes sont nuls.
, formée de 1 en dernière ligne et dernière colonne, les autres termes sont nuls.
On note ![]() l’endomorphisme canoniquement associé à A.
l’endomorphisme canoniquement associé à A.
![]()
![]() car les colonnes
car les colonnes ![]() et
et ![]() de
de ![]() forment une famille libre et pour tout
forment une famille libre et pour tout ![]() ,
, ![]() .
.
Donc 0 est valeur propre de ![]() et
et ![]() .
.
Si ![]() .
.
La famille libre (car échelonnée) ![]() de
de ![]() a un cardinal égal à
a un cardinal égal à ![]() . C’est une base de
. C’est une base de ![]() .
.
![]() On résout ensuite
On résout ensuite ![]() avec
avec ![]() et
et ![]() ,
, ![]() .
.
![]()
![]()
![]()
![]() et
et ![]()
![]()
![]() ,
, ![]() et
et ![]()
![]()
![]() ,
, ![]() et
et ![]() .
.
Il est donc nécessaire que
![]() sinon
sinon ![]()
et alors ![]() , donc
, donc ![]() ce qui est absurde.
ce qui est absurde.
Les deux dernières valeurs propres sont ![]() et
et ![]() .
.
Un vecteur propre de ![]() associé à la valeur propre
associé à la valeur propre ![]() est
est ![]() et à la valeur propre
et à la valeur propre ![]() est
est ![]() .
.
![]() Comme
Comme ![]()
![]() ,
,
![]() est diagonalisable et
est diagonalisable et ![]() avec
avec ![]() et
et
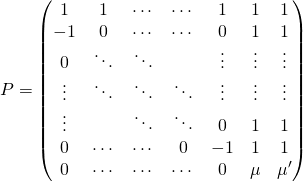 .
.
Anticipez les révisions à venir, qui vont être indispensables pour les concours post-prépa, en vous reportant aux cours en ligne de Maths en PSI, aux cours en ligne de Maths en MP et aux cours en ligne de Maths en PC, tous gratuits et accessibles depuis ordinateur, tablette et smartphone.
2. Des exemples pratiques de trigonalisation
Exercice 4
Trigonaliser 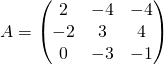 .
.
Corrigé de l’exercice 4 :
Soit ![]() la base canonique de
la base canonique de ![]() et
et ![]() l’endomorphisme canoniquement associé à
l’endomorphisme canoniquement associé à ![]() .
.
![]()
![]() ,
, ![]()
Si ![]() ,
, 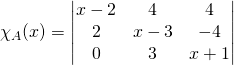
On le développe suivant la première colonne :
![]()
![]()
![]() .
.
Donc Sp![]() .
.
![]() On résout
On résout ![]()
![]()
![]()
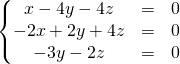
![]()
![]()
Le sous-espace propre associé à la valeur propre 1 est de dimension 1, donc ![]() nest pas diagonalisable et
nest pas diagonalisable et ![]() vérifie
vérifie ![]() .
.
![]() On résout
On résout ![]()
![]()
![]()
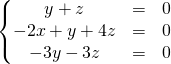
![]()
![]()
![]() vérifie
vérifie ![]()
![]() On complète la famille libre
On complète la famille libre ![]() de façon à obtenir une base de
de façon à obtenir une base de ![]() .
.
On pose ![]() ,
, ![]() est une base de
est une base de ![]() car la matrice
car la matrice ![]() de la famille
de la famille ![]() dans la base canonique
dans la base canonique 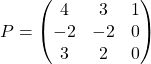 est inversible (son déterminant est égal à 2).
est inversible (son déterminant est égal à 2).
On décompose ![]() dans la base
dans la base ![]() en cherchant les réels
en cherchant les réels ![]() tels que
tels que ![]()
ce qui donne le système :
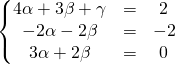
![]()
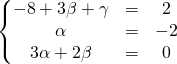
ce qui donne ![]() soit
soit ![]()
![]() La matrice de
La matrice de ![]() dans la base
dans la base ![]() est
est
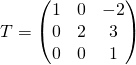 .
.
![]() avec
avec 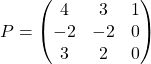 .
.
Les matrices ![]() et
et ![]() sont semblables.
sont semblables.
Exercice 5
Trigonaliser la matrice 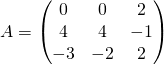 .
.
Corrigé de l’exercice 5 :
![]() Si
Si ![]() ,
, 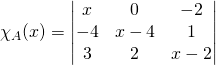
En développant suivant la première ligne,
![]() .
.
![]() On introduit la matrice
On introduit la matrice ![]()
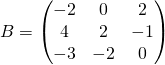 .
.
On calcule 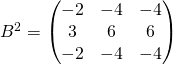 .
.
![]() et
et ![]() (cf. théorème de Cayley-Hamilton).
(cf. théorème de Cayley-Hamilton).
![]() Si
Si ![]() est l’endomorphisme canoniquement associé à
est l’endomorphisme canoniquement associé à ![]() et si
et si ![]() ,
, ![]() .
.
On démontre que ![]() est une base de
est une base de ![]() en introduisant la matrice
en introduisant la matrice ![]() de la famille
de la famille ![]() dans la base canonique :
dans la base canonique :
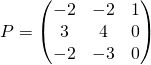 avec
avec ![]() .
.
La matrice ![]() de
de ![]() dans cette base
dans cette base ![]() est
est 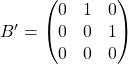
et ![]() où
où ![]() est définie ci-dessus.
est définie ci-dessus.
![]() donc
donc ![]() .
.
On a trigonalisé la matrice ![]() .
.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
3. Application des résultats sur la diagonalisation.
Exercice 6 (suite du 1)
On rappelle que 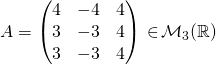 vérifie
vérifie ![]() avec
avec
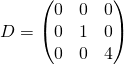 et
et 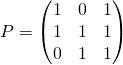 .
.
Question 1
Résoudre l’équation ![]() où
où ![]() .
.
Question 2
Trouver les sous-espaces ![]() -stables lorsque
-stables lorsque ![]() est l’endomorphisme canoniquement associé à
est l’endomorphisme canoniquement associé à ![]() .
.
Corrigé de l’exercice 6 :
1/ On note ![]() ,
, ![]() l’endomorphisme canoniquement associé à
l’endomorphisme canoniquement associé à ![]() .
.
Analyse :
On suppose que ![]() est telle que
est telle que ![]() . L’endomorphisme
. L’endomorphisme ![]() canoniquement associé à
canoniquement associé à ![]() vérifie
vérifie ![]() .
.
Alors ![]() .
.
Les sous espaces propres de ![]() sont
sont ![]() stables.
stables.
On écrit pour ![]() ,
, ![]()
Comme ![]() ,
, ![]() est combinaison linéaire de
est combinaison linéaire de ![]() , donc il existe
, donc il existe ![]() tel que
tel que ![]() .
.
Puis en écrivant que ![]() , on obtient
, on obtient ![]() .
.
Synthèse :
Soit ![]() et
et ![]() l’endomorphisme défini par
l’endomorphisme défini par
![]() ,
, ![]() et
et ![]() , alors
, alors ![]() car les applications linéaires
car les applications linéaires ![]() et
et ![]() sont égales sur la base de vecteurs propres.
sont égales sur la base de vecteurs propres.
En traduisant matriciellement ce résultat, l’équation ![]() admet 4 solutions
admet 4 solutions ![]() où
où 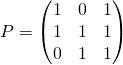 où
où ![]() .
.
2/ ![]() Il est évident que
Il est évident que ![]() et
et ![]() sont
sont ![]() -stables.
-stables.
![]() On sait que les droites
On sait que les droites ![]() -stables sont les droites engendrées par un vecteur propre de
-stables sont les droites engendrées par un vecteur propre de ![]() . Il y en a trois :
. Il y en a trois : ![]() ,
, ![]() ,
, ![]() .
.
![]() Soit
Soit ![]() un plan
un plan ![]() -stable. On peut introduire l’endomorphisme
-stable. On peut introduire l’endomorphisme ![]() induit par
induit par ![]() sur
sur ![]() . Son polynôme caractéristique divise le polynôme caractéristique de
. Son polynôme caractéristique divise le polynôme caractéristique de ![]() . Il est donc scindé à racines simples. Alors
. Il est donc scindé à racines simples. Alors ![]() est diagonalisable et
est diagonalisable et ![]() admet une base formée de deux vecteurs propres de
admet une base formée de deux vecteurs propres de ![]() donc de
donc de ![]() .
.
Réciproquement, si ![]() est un plan engendré par deux vecteurs propres non colinéaires de
est un plan engendré par deux vecteurs propres non colinéaires de ![]() , il est
, il est ![]() -stable.
-stable.
On note ![]() ,
, ![]() et
et ![]() , il y a trois plans
, il y a trois plans ![]() -stables :
-stables : ![]() ,
, ![]() et
et ![]() .
.
Exercice 7 (suite du 4)
Déterminer les sous-espaces vectoriels ![]() -stables lorsque
-stables lorsque ![]() est l’endomorphisme canoniquement associé à
est l’endomorphisme canoniquement associé à ![]() où
où 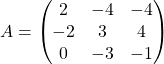 .
.
Corrigé de l’exercice 7 :
On note ![]() la base canonique de
la base canonique de ![]() .
.
On a démontré dans l’exercice 4 que ![]() et que les sous espaces propres sont de dimension 1.
et que les sous espaces propres sont de dimension 1.
![]() vérifie
vérifie ![]()
![]() vérifie
vérifie ![]() .
.
![]() Il est évident que
Il est évident que ![]() et
et ![]() sont
sont ![]() -stables.
-stables.
![]() On cherche les droites
On cherche les droites ![]() – stables, elles sont engendrées par un vecteur propre de
– stables, elles sont engendrées par un vecteur propre de ![]() .
.
Il y a deux droites ![]() -stables :
-stables : ![]() et
et ![]() .
.
![]() On cherche les plans
On cherche les plans ![]() -stables. Ils ont une équation de la forme
-stables. Ils ont une équation de la forme ![]() où
où ![]() est un vecteur propre de
est un vecteur propre de ![]() . (justification à donner voir la démonstration dans le paragraphe 6 du chapitre méthodes).
. (justification à donner voir la démonstration dans le paragraphe 6 du chapitre méthodes).
![]() et
et ![]() ont même polynôme caractéristique. Les valeurs propres de
ont même polynôme caractéristique. Les valeurs propres de ![]() sont 1 et 2.
sont 1 et 2.
![]()
![]()
![]()
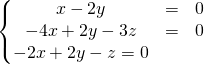
![]()
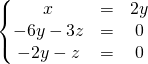
Un vecteur propre associé à la valeur propre 1 est 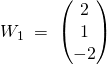
![]()
![]()
![]()
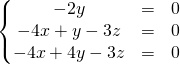
![]()
![]()
Un vecteur propre associé à la valeur propre 2 est 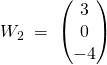
![]() On obtient deux plans
On obtient deux plans ![]() -stables d’équations :
-stables d’équations : ![]() et
et ![]() .
.
Le premier plan est engendré par les vecteurs ![]() et
et ![]() .
.
Le deuxième plan est engendré par les vecteurs ![]() et
et ![]() .
.
4. Diagonalisation ou trigonalisation de matrices non explicites
Exercice 8 (MinesPonts PSI 2016)
Trouver une CNS sur les complexes ![]() pour que
pour que ![]() soit diagonalisable avec
soit diagonalisable avec 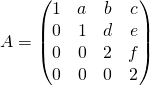 .
.
Corrigé de l’exercice 8 :
Comme![]() est triangulaire, il est évident que
est triangulaire, il est évident que ![]() .
.
![]() est diagonalisable ssi
est diagonalisable ssi ![]() est un polynôme annulateur de
est un polynôme annulateur de ![]() .
.
![]()
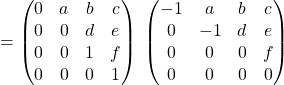
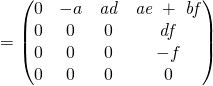
on obtient donc la CNS ![]() .
.
Exercice 9 TPE 2017 .
Soit ![]() . On considère une matrice
. On considère une matrice ![]() telle
telle ![]() ,
, ![]() et
et ![]() .
.
Question 1
Le nombre de valeurs propres distinctes de ![]() est égal
est égal
Question 2
![]() est diagonalisable.
est diagonalisable.
Corrigé de l’exercice 9 :
1/ 0 est valeur propre d’ordre au moins égal à ![]() .
.
Le polynôme caractéristique de ![]() est divisible par
est divisible par ![]() , il est scindé sur
, il est scindé sur ![]() et il existe
et il existe ![]() et
et ![]()
![]() tels que
tels que ![]()
La somme des valeurs propres est égale à ![]() et aussi à
et aussi à ![]() , donc
, donc ![]() .
.
Si l’on avait ![]() = 0, on aurait
= 0, on aurait ![]() par le théorème de Cayley Hamilton, on aurait
par le théorème de Cayley Hamilton, on aurait ![]() ce qui est exclu.
ce qui est exclu.
Les valeurs propres de ![]() sont 0 (d’ordre
sont 0 (d’ordre ![]() ),
), ![]() et
et ![]() où
où ![]() est un complexe non nul.
est un complexe non nul.
2/ Comme ![]() et
et ![]() , la somme des dimensions des sous-espaces propres de
, la somme des dimensions des sous-espaces propres de ![]() étant égale à
étant égale à ![]() ,
, ![]() est diagonalisable.
est diagonalisable.
5. Diagonalisation d’une matrice par blocs
Exercice 10
Question 1
Étudier la diagonalisation de ![]()
Question 2
Soit ![]() , montrer que
, montrer que ![]() est diagonalisable.
est diagonalisable.
Question 3
Soit ![]() telle que
telle que ![]() soit diagonalisable. Montrer que
soit diagonalisable. Montrer que ![]() est diagonalisable.
est diagonalisable.
Corrigé de l’exercice 10 :
1/ ![]() ;
; ![]() est scindé à racines simples, donc
est scindé à racines simples, donc ![]() est diagonalisable.
est diagonalisable.
![]() ,
,
![]() .
.
On peut donc écrire ![]() avec
avec ![]() ,
, ![]() et
et ![]() .
.
2/ ![]() étant diagonalisable, il existe
étant diagonalisable, il existe ![]() et
et ![]() diagonale telles que
diagonale telles que ![]() .
.
On note ![]() et
et ![]() .
.
Comme ![]() ,
,
![]() est inversible d’inverse
est inversible d’inverse ![]() .
.
![]()
![]()
![]() .
.
Puis on vérifie facilement que
![]() avec
avec ![]() et
et ![]() .
.
Donc ![]() avec
avec ![]() diagonale.
diagonale.
On a prouvé que ![]() est diagonalisable.
est diagonalisable.
3/ En utilisant les résultats du début de la deuxième question, ![]() est semblable à
est semblable à ![]() , donc
, donc ![]() est diagonalisable.
est diagonalisable.
Il existe un polynôme ![]() scindé à racines simples tel que
scindé à racines simples tel que ![]() .
.
Un calcul simple de matrices par blocs donne ![]() ,
, ![]() est diagonalisable.
est diagonalisable.
Puisque les cours de maths en Maths Spé nécessitent parfois d’être revus et complétés, les cours en ligne sont le parfait complément pour maximiser ses révisions et bien évidemment ses résultats. Quelques cours que vous pourriez réviser :
- les matrices
- les espaces vectoriels normés
- les suites et séries de fonctions
- l’intégration sur un intervalle quelconque
- les séries entières
Si vous souhaitez accéder à l’ensemble des exercices, annales et aux corrigés, n’hésitez pas à télécharger l’application PrepApp

