Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Les séries numériques MP, PC, PSI, PT
Résumé de cours Exercices et corrigés
Exercices et corrigés – séries numériques
1. Nature de quelques séries
Exercice 1 sur la nature des séries numériques
Nature de la série de terme général ![]()
Corrigé de l’exercice 1 :
On cherche la limite de ![]() pour cela on commence par étudier
pour cela on commence par étudier ![]()
![]()
On a une somme de termes qui divergent vers ![]() , on factorise par celui qui tend le plus vite vers
, on factorise par celui qui tend le plus vite vers ![]() :
:
![]() où
où ![]()
![]()
Par croissance comparée, ![]() et donc
et donc ![]() .
.
On a prouvé que ![]() , donc
, donc ![]() , par domination par une série de Riemann convergente,
, par domination par une série de Riemann convergente, ![]() converge.
converge.
Exercice 2 : somme d’une série numérique
Soient ![]() et
et ![]() deux réels strictement positifs et
deux réels strictement positifs et ![]() .
.
Nature de ![]() .
.
Corrigé de l’exercice 2 :
![]() Si
Si ![]() ,
, ![]() car
car
![]() où
où ![]() ,
,
donc ![]()
![]() Si
Si ![]() ,
, ![]()
par domination par une série géométrique convergente, ![]() converge et par équivalence de séries de réels positifs,
converge et par équivalence de séries de réels positifs, ![]() converge.
converge.
![]() Si
Si ![]() , alors
, alors ![]() , donc par minoration par une série de Riemann divergente,
, donc par minoration par une série de Riemann divergente, ![]() diverge et par équivalence de séries de réels positifs,
diverge et par équivalence de séries de réels positifs, ![]() diverge.
diverge.
![]() Si
Si ![]() ,
, ![]() car
car ![]() où
où ![]() (croissance comparée), donc
(croissance comparée), donc ![]() .
.
Par équivalence à une série géométrique positive, ![]() converge ssi
converge ssi ![]() .
.
En résumé , ![]() converge ssi
converge ssi
(![]() et
et ![]() )
)
ou (![]() et
et ![]() ).
).
Exercice 3 : étude d’une série numérique
Étudier la série de terme général ![]() avec
avec ![]() .
.
Corrigé de l’exercice 3 :
![]() Si
Si ![]() ,
, ![]() , donc
, donc ![]() diverge grossièrement.
diverge grossièrement.
![]() Si
Si ![]() ,
, ![]() , donc
, donc ![]() alors
alors ![]() diverge par minoration par une série divergente.
diverge par minoration par une série divergente.
![]() Si
Si ![]() , soit
, soit 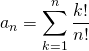 .
.
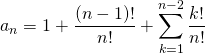
et 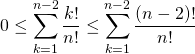
donc ![]() .
.
Par encadrement, la suite ![]() converge vers 1, alors
converge vers 1, alors
![]()
![]() .
.
Donc ![]() converge par équivalence à une série de Riemann convergente.
converge par équivalence à une série de Riemann convergente.
Exercice 4 : nature d’une série numérique
Nature de la série de terme général ![]() .
.
Corrigé de l’exercice 4 :
![]() .
.
En utilisant le développement limité de ![]() à l’ordre 2 en 0, il est important que le terme complémentaire soit un O, pour ne pas devoir écrire le DL à l’ordre 3 :
à l’ordre 2 en 0, il est important que le terme complémentaire soit un O, pour ne pas devoir écrire le DL à l’ordre 3 :
![]()
![]()
![]()
donc ![]()
et comme ![]() et
et ![]()
![]()
![]()
La série de terme général ![]() converge par le théorème spécial des séries alternées.
converge par le théorème spécial des séries alternées.
La série de terme général ![]() converge absolument par domination.
converge absolument par domination.
Donc par somme, ![]() converge.
converge.
D’autres cours en ligne de Maths en PC, des cours en ligne de MP en Maths et aussi des cours en ligne de Maths en PSI sont consultables gratuitement afin de permettre à tous les étudiants en Maths Spé de pouvoir progresser et/ou se remettre à niveau rapidement.
2. Comparaison suite-série
Soit une suite ![]() de réels strictement positifs. on définit la suite
de réels strictement positifs. on définit la suite ![]() par
par
![]() et si
et si ![]() .
.
Donner une CNS sur ![]() pour que la suite
pour que la suite ![]() converge.
converge.
Corrigé de l’exercice :
Par une récurrence simple, ![]() ,
,
donc ![]() .
.
La suite ![]() est strictement croissante.
est strictement croissante.
![]() Si la suite
Si la suite ![]() converge vers
converge vers ![]() , comme
, comme ![]() , on en déduit que
, on en déduit que ![]() .
.
La série de terme général ![]() converge, donc la série de terme général
converge, donc la série de terme général ![]() converge.
converge.
Puis ![]() , la série de terme général
, la série de terme général ![]() converge.
converge.
![]() Si
Si ![]() converge, en écrivant puisque
converge, en écrivant puisque ![]() et
et ![]() :
: ![]() , la série de terme général
, la série de terme général ![]() converge par domination, donc la suite
converge par domination, donc la suite ![]() converge.
converge.
Conclusion : la suite ![]() converge ssi
converge ssi ![]() converge.
converge.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
3. Comparaison d’une série numérique avec une intégrale
Soit ![]() et si
et si ![]() ,
, ![]() .
.
On note 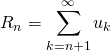 , montrer que
, montrer que ![]() .
.
Corrigé de l’exercice :
On note ![]() : [1 ,
: [1 , ![]() [
[ ![]() ,
, ![]() .
.
![]() est décroissante.
est décroissante.
Si ![]() , pour tout
, pour tout ![]() ,
, ![]() ,
,
en intégrant sur ![]() ,
, ![]()
alors si ![]() ,
, ![]()
Soit ![]() , si
, si ![]() , on somme pour
, on somme pour ![]() , on obtient :
, on obtient :
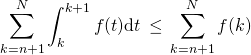
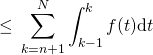
puis par la relation de Chasles,
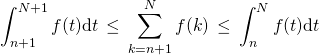
avec ![]()
![]()
(![]() ). Donc
). Donc
![]()
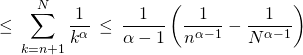
Lorsque ![]() tend vers
tend vers ![]() , on obtient
, on obtient
![]()
Donc par multiplication par ![]() :
:
![]()
Par encadrement, ![]()
donc ![]() .
.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
4 – Transformation d’ Abel
Question 1
Soient ![]() et
et ![]() deux suites telles que :
deux suites telles que :
![]() la suite
la suite ![]() est une suite de réels décroissante, convergente de limite nulle
est une suite de réels décroissante, convergente de limite nulle
![]() la suite
la suite ![]() est une suite de complexes telle que si l’on note, pour
est une suite de complexes telle que si l’on note, pour ![]() ,
, 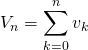 , la suite
, la suite ![]() est bornée.
est bornée.
a) On note si ![]() ,
, 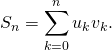
Montrer que ![]() vérifie :
vérifie :
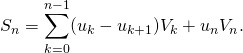
b) Montrer que ![]() converge.
converge.
Question 2
Utiliser la première question, pour montrer que si la suite ![]() est une suite de réels décroissante, convergente de limite nulle,
est une suite de réels décroissante, convergente de limite nulle, ![]() est convergente.
est convergente.
Question 3
a) Montrer que ![]() , la série de terme général
, la série de terme général ![]() converge.
converge.
b) Montrer que pour tout ![]() et
et ![]() , les séries de termes généraux
, les séries de termes généraux ![]() et
et ![]() convergent.
convergent.
c) Montrer que si ![]() et
et ![]() , la série de terme général
, la série de terme général ![]() ne converge pas absolument.
ne converge pas absolument.
(on pourra comparer ![]() et
et ![]() ).
).
Corrigé de l’exercice sur la transformation d’Abel :
a) On peut aussi raisonner par récurrence ou démontrer comme ici entièrement la formule.
Si ![]() ,
, 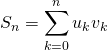
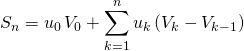 .
.
On a utilisé si ![]() et
et ![]() .
. 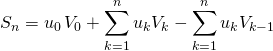 .
.
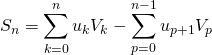
(avec ![]() ).
).
Soit 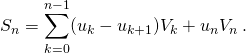
b) Soit ![]() tel que pour tout
tel que pour tout ![]() ,
, ![]() , donc
, donc ![]() (produit d’une suite bornée et d’une suite qui converge vers 0).
(produit d’une suite bornée et d’une suite qui converge vers 0).
Soit 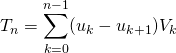 .
.
![]() est la somme partielle d’ordre
est la somme partielle d’ordre ![]() de la série de terme général
de la série de terme général ![]() avec
avec
![]()
![]() .
.
Comme la suite de terme général ![]() converge, la série de terme général
converge, la série de terme général ![]() converge, donc la série de terme général
converge, donc la série de terme général ![]() converge absolument, on en déduit que la suite
converge absolument, on en déduit que la suite ![]() converge.
converge.
On remarque que l’on retrouve une partie du théorème des séries alternées.3/
On note
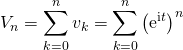 ; comme
; comme on obtient après quotient et simplification,
donc
La suite
où
N’attendez pas le dernier moment pour vos révisions, et revoyez les notions de maths les plus importantes au programme de Maths Spé avec nos cours de Maths en ligne :
Si vous souhaitez accéder à l’ensemble des exercices, annales et aux corrigés des exemples, n’hésitez pas à télécharger l’application PrepApp

