Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Familles sommables pour les MP
Résumé de cours Exercices Corrigés
Résumé de cours et méthodes – Familles sommables
1. Les familles de réels positifs indexées par un ensemble dénombrable
1.1. Définition d’une famille sommable de réels positifs ou nuls
def : La famille ![]() de réels positifs ou nuls, indexée par un ensemble
de réels positifs ou nuls, indexée par un ensemble ![]() dénombrable, est dite sommable si
dénombrable, est dite sommable si 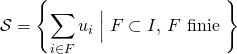
est majoré dans ce cas, la somme de la famille ![]() est
est ![]() .
.
Si la famille ![]() n’est pas sommable, on note
n’est pas sommable, on note ![]() .
.
Conséquence pratique :
Soit ![]() et
et ![]() une famille dénombrable de réels positifs ou nuls.
une famille dénombrable de réels positifs ou nuls.
Pour démontrer que la famille ![]() est sommable, il suffit de prouver qu’il existe un réel
est sommable, il suffit de prouver qu’il existe un réel ![]() tel que
tel que 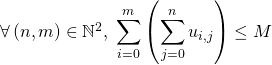 ,
,
car toute partie finie de ![]() est contenue dans une partie de la forme
est contenue dans une partie de la forme ![]() .
.
Exemple :
La famille ![]() est-elle sommable ?
est-elle sommable ?
1.2. Propriétés
P1 : Soient ![]() et
et ![]() deux familles dénombrables de réels positifs ou nuls.
deux familles dénombrables de réels positifs ou nuls.
Si pour tout ![]() et si la famille
et si la famille ![]() est sommable, la famille
est sommable, la famille ![]() est sommable et de plus
est sommable et de plus ![]() .
.
P2 : Soit ![]() une suite de réels positifs ou nuls, la famille
une suite de réels positifs ou nuls, la famille ![]() est sommable si, et seulement si, la série de terme général
est sommable si, et seulement si, la série de terme général ![]() est convergente. Dans ce cas,
est convergente. Dans ce cas, 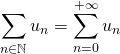 .
.
1.3. Théorème de sommation par paquets
Théorème de sommation par paquets :
Si ![]() est une partition de
est une partition de ![]() et
et ![]() une famille de réels positifs, alors la famille
une famille de réels positifs, alors la famille ![]() est sommable si, et seulement si,
est sommable si, et seulement si,
![]() pour tout entier
pour tout entier ![]() , la famille
, la famille ![]() est sommable.
est sommable.
![]() la série
la série 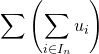 converge.
converge.
Dans ce cas, 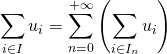 .
.
Exemples de choix de partition
![]() Pour
Pour ![]() , on peut choisir si
, on peut choisir si ![]()
![]() ,
, ![]() ,
,
ou ![]() .
.
![]() Pour
Pour ![]() , on peut choisir si
, on peut choisir si ![]() .
.
COURS DE MATHS A DOMICILE
Les meilleurs profs de maths pour
réussir sa scolarité
En ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
2. Cas des familles de complexes indexées par un ensemble dénombrable
2.1. Définition d’une famille sommable et de la somme
def : La famille ![]() de réels de signe quelconque ou de complexes, indexée par un ensemble
de réels de signe quelconque ou de complexes, indexée par un ensemble ![]() dénombrable, est dite sommable lorsque la famille de réels positifs ou nuls
dénombrable, est dite sommable lorsque la famille de réels positifs ou nuls ![]() est sommable.
est sommable.
Définition de la somme dans le cas d’une famille sommable :
![]() Dans le cas d’une famille sommable
Dans le cas d’une famille sommable ![]() de réels de signe quelconque, on définit pour tout
de réels de signe quelconque, on définit pour tout ![]() ,
, ![]() et
et ![]()
alors ![]() et
et ![]() .
.
On en déduit que ![]() .
.
Les familles ![]() et
et ![]() sont des familles sommables de réels positifs. On pose :
sont des familles sommables de réels positifs. On pose :
![]() .
.
![]() Dans le cas d’une famille sommable
Dans le cas d’une famille sommable ![]() de complexes, on note pour tout
de complexes, on note pour tout ![]() ,
, ![]() .
.
Les familles ![]() et
et ![]() sont des familles sommables de réels et on pose
sont des familles sommables de réels et on pose
![]() .
.
2.2. Propriétés des familles sommables
P1 : Soit ![]() une suite complexe, la famille
une suite complexe, la famille ![]() est sommable si, et seulement si, la série de terme général
est sommable si, et seulement si, la série de terme général ![]() est convergente.
est convergente.
Dans ce cas, 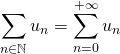 .
.
P2 : Soient ![]() et
et ![]() deux familles sommables de complexes et
deux familles sommables de complexes et ![]() et
et ![]() deux complexes.
deux complexes.
La famille ![]() est sommable et
est sommable et ![]() .
.
Théorème de sommation par paquets :
Si ![]() est une partition de
est une partition de ![]() et
et ![]() une famille sommable de complexes, alors,
une famille sommable de complexes, alors,
![]() pour tout entier
pour tout entier ![]() , la famille
, la famille ![]() est sommable.
est sommable.
![]() la série
la série 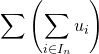 converge.
converge.
![]()
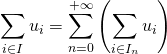 .
.
2.3. Application aux suites doubles.
Théorème de Fubini pour les suites doubles de réels positifs ou nuls :
La famille ![]() de réels positifs ou nuls est sommable
de réels positifs ou nuls est sommable
si, et seulement si,
a) pour tout ![]() , la série
, la série ![]() est convergente de somme notée
est convergente de somme notée ![]() ,
,
b) la série de terme général ![]() est convergente,
est convergente,
si, et seulement si,
a) pour tout ![]() , la série
, la série ![]() est convergente de somme notée
est convergente de somme notée ![]() ,
,
b) la série de terme général ![]() est convergente.
est convergente.
Dans ce cas :
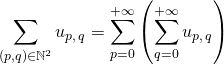 .
.
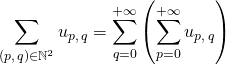 .
.
Les différents cours en ligne de MP en Maths, les cours en ligne de PC en Maths et les cours en ligne de PSI en Maths, permettent aux étudiants de ne pas rester bloqués sur leur cours. Les définitions, les exemples et les méthodes présentent dans les cours en ligne permettent de faciliter la compréhension du cours.
Théorème de Fubini pour les suites doubles de complexes :
Soit ![]() une suite double sommable de complexes. Alors :
une suite double sommable de complexes. Alors :
a) pour tout ![]() , la série
, la série ![]() est convergente de somme notée
est convergente de somme notée ![]() ,
,
b) la série de terme général ![]() est convergente,
est convergente,
et
a) pour tout ![]() , la série
, la série ![]() est convergente de somme notée
est convergente de somme notée ![]() ,
,
b) la série de terme général ![]() est convergente.
est convergente.
De plus,
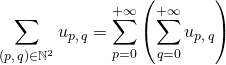
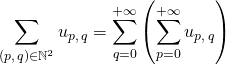 .
.
Remarque : Soit ![]() une suite double de réels positifs ou nuls, si
une suite double de réels positifs ou nuls, si 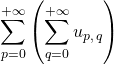 est défini, la famille double
est défini, la famille double ![]() est sommable et
est sommable et 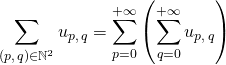
et 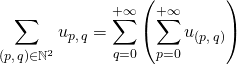 .
.
P3 : Soient ![]() et
et ![]() deux suites complexes. Pour que la famille double
deux suites complexes. Pour que la famille double ![]() soit sommable, il suffit que les séries de termes généraux
soit sommable, il suffit que les séries de termes généraux ![]() et
et ![]() soient absolument convergentes. Dans ce cas :
soient absolument convergentes. Dans ce cas :
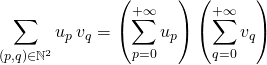 .
.
P4 : Produit de Cauchy
Soient ![]() et
et ![]() deux suites complexes. On suppose que les séries
deux suites complexes. On suppose que les séries ![]() et
et ![]() sont absolument convergentes.
sont absolument convergentes.
On note ![]() , la série produit de Cauchy de terme général
, la série produit de Cauchy de terme général ![]() est absolument convergente et
est absolument convergente et
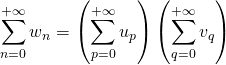 .
.
UN PROF DE MATHS POUR EXCELLER
La pratique et la compréhension
clés de la réussite
Cours de maths en ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
Exercices sur les familles sommables
1. Sommables ou pas
Exercice 1
La famille ![]() est-elle sommable ?
est-elle sommable ?
2. Une première famille double
Exercice 2 :
On note ![]() si
si ![]() et
et ![]() si
si ![]() .
.
1. La suite double ![]() est sommable ?
est sommable ?
2. Les réels 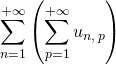 et
et 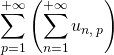 sont définis.
sont définis.
3. 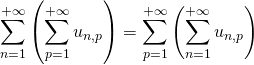
Corrigés sur les familles sommables :
Exercice 1 :
On note ![]() .
.
![]() est une partition de
est une partition de ![]() .
.![]()
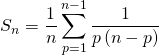 .
.
Par décomposition en éléments simples, 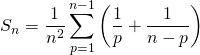 .
.
En posant ![]() ,
, 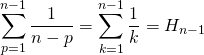
![]() .On a le résultat classique
.On a le résultat classique 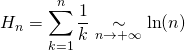 .
.
![]() ,
,
alors ![]() , donc
, donc ![]() converge.
converge.
En utilisant le théorème de sommation par paquets, la famille est sommable.
Même en fin d’année il est important de réviser les cours vus en début d’année, car lors des concours, la connaissance de tous les chapitres sera obligatoire pour arriver dans les meilleurs et être admis dans l’école de son choix. N’oubliez pas, par exemple, de réviser régulièrement les chapitres suivants que vous avez la possibilité de reviser lors de nos cours de maths :

