Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Fonctions de plusieurs variables en MP, PC, PSI et PT
Résumé de cours Exercices Corrigés
Résumé de cours et méthodes – Fonctions de plusieurs variables
1. Calcul de la dérivée suivant un vecteur
Hypothèses : ![]() est définie sur un ouvert
est définie sur un ouvert ![]() d’un espace vectoriel
d’un espace vectoriel ![]() de dimension finie à valeurs dans un
de dimension finie à valeurs dans un ![]() ev
ev ![]() de dimension finie.
de dimension finie.
![]() ,
, ![]() est un vecteur non nul de
est un vecteur non nul de ![]() .
.
On veut justifier l’existence de la dérivée de ![]() en
en ![]() selon
selon ![]()
![]() M1 : Démontrer que
M1 : Démontrer que ![]() admet une dérivée partielle suivant le vecteur
admet une dérivée partielle suivant le vecteur ![]() revient à prouver que la fonction
revient à prouver que la fonction ![]() est dérivable en
est dérivable en ![]() .
.
Dans ce cas, la dérivée de ![]() en
en ![]() suivant le vecteur
suivant le vecteur ![]() est définie par
est définie par
![]() .
.
![]() M1.B :
M1.B : ![]() et si
et si ![]() est la base canonique de
est la base canonique de ![]() , pour tout
, pour tout ![]() , la dérivée de
, la dérivée de ![]() en
en ![]() suivant
suivant ![]() est la
est la ![]() -ème dérivée partielle de
-ème dérivée partielle de ![]() en
en ![]() et notée
et notée ![]() ou
ou ![]() .
.
Il est indispensable d’utiliser la limite de ![]() pour calculer
pour calculer ![]() lorsque
lorsque ![]() est définie par des conditions du type
est définie par des conditions du type ![]() si
si ![]() et
et ![]() .
.
Lorsque ![]() , démontrer que
, démontrer que ![]() existe revient à démontrer que la
existe revient à démontrer que la ![]() -ème application partielle de
-ème application partielle de ![]() en
en ![]() soit
soit ![]() ,
,
![]() est dérivable en
est dérivable en ![]() .
.
![]() M2 : On sait que
M2 : On sait que ![]() est différentiable en
est différentiable en ![]() , alors
, alors ![]() .
.
![]() M3 :
M3 : ![]() et
et ![]() est de classe
est de classe ![]() en
en ![]() , si
, si ![]() ,
,
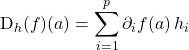 .
.
![]() peut avoir une dérivée suivant tout vecteur en un point sans être différentiable en
peut avoir une dérivée suivant tout vecteur en un point sans être différentiable en ![]() .
.
exemple : ![]() et
et ![]() . Étudier la dérivée de
. Étudier la dérivée de ![]() suivant un vecteur
suivant un vecteur ![]() en
en ![]() .
.
UN PROF DE MATHS POUR EXCELLER
La pratique et la compréhension
clés de la réussite
Cours de maths en ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
2. Problèmes de différentiabilité
2.1. En utilisant la définition
Hypothèse : ![]() est définie sur un ouvert
est définie sur un ouvert ![]() d’un
d’un ![]() espace vectoriel
espace vectoriel ![]() de dimension finie à valeurs dans un
de dimension finie à valeurs dans un ![]() ev
ev ![]() de dimension finie et
de dimension finie et ![]() .
.
![]() M1 En appliquant la définition :
M1 En appliquant la définition :
![]() est différentiable en
est différentiable en ![]() s’il existe une application linéaire
s’il existe une application linéaire ![]() de
de ![]() dans
dans ![]() et un voisinage
et un voisinage ![]() de
de ![]() tel que si
tel que si ![]() ,
, ![]() .
.
En particulier dans le cas où ![]() ,
,
![]() calculer pour tout
calculer pour tout ![]() ,
, ![]()
![]() introduire
introduire ![]() et former
et former
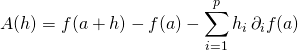
![]() vérifier que
vérifier que 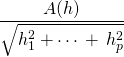 admet
admet ![]() pour limite lorsque
pour limite lorsque ![]() .
.
Conséquence : avec les notations précédentes, ![]() est unique et appelée différentielle de
est unique et appelée différentielle de ![]() en
en ![]() et notée
et notée ![]() .
.
On allège les notations en écrivant ![]()
exemple 1 :
Si ![]() et si
et si ![]() , montrer que
, montrer que ![]() est différentiable en tout
est différentiable en tout ![]() .
.
2.1. En utilisant les théorèmes
![]() M2. Appliquer les théorèmes pour démontrer que
M2. Appliquer les théorèmes pour démontrer que ![]() est différentiable en
est différentiable en ![]() :
:
![]() combinaison linéaire de fonctions de fonctions différentiables en
combinaison linéaire de fonctions de fonctions différentiables en ![]() ,
,
avec ![]()
![]() produit de deux fonctions différen- tiables en
produit de deux fonctions différen- tiables en ![]() à valeurs dans
à valeurs dans ![]() ,
,
![]()
![]() quotient de 2 fonctions différentia- bles en
quotient de 2 fonctions différentia- bles en ![]() et à valeurs dans
et à valeurs dans ![]() , le dénominateur ne s’annulant pas,
, le dénominateur ne s’annulant pas,
![]()
![]() .
.
![]() composée de fonctions différentia- bles :
composée de fonctions différentia- bles :
hyp : ![]() différentiable en
différentiable en ![]() ,
, ![]() et
et ![]() différentiable en
différentiable en ![]()
conclusion : ![]() est différentiable en
est différentiable en ![]() et
et ![]()
![]() restriction à un ouvert d’une application linéaire
restriction à un ouvert d’une application linéaire ![]()
pour tout ![]() ,
, ![]() .
.
![]() Cas où
Cas où ![]() ,
, ![]() étant différentiable en
étant différentiable en ![]() à valeurs dans
à valeurs dans ![]() et
et ![]() étant différentiable en
étant différentiable en ![]() à valeurs dans
à valeurs dans ![]() ,
, ![]() étant bilinéaire sur
étant bilinéaire sur ![]() .
.
![]()
![]()
Application si ![]() et si
et si ![]() ,
,
en introduisant l’application bilinéaire ![]() et les applications linéaires
et les applications linéaires ![]() ,
, ![]() est différentia- ble en
est différentia- ble en ![]() et
et
![]() .
.
![]() M2. En démontrant que la fonction est de classe
M2. En démontrant que la fonction est de classe ![]() sur
sur ![]() .
.
Les cours en ligne de Maths en MP, les cours en ligne de Maths en PC et les cours en ligne de PSI en Maths comme les cours en ligne de Maths en PT et les cours de maths à Paris sont des aides pour les étudiants de Maths Spé. Ils ne remplacent pas les cours dispensés en prépa, en revanche, ils permettent de les compléter pour améliorer vos connaissances et donc vos notes.
3. Fonctions de classe 
3.1. Démontrer que ![]() est de classe
est de classe ![]()
Hypothèse : ![]() est définie sur un ouvert
est définie sur un ouvert ![]() d’un
d’un ![]() -espace vectoriel
-espace vectoriel ![]() de dimension finie à valeurs dans un
de dimension finie à valeurs dans un ![]() -ev de dimension finie et
-ev de dimension finie et ![]() .
.
Pour démontrer que ![]() est de classe
est de classe ![]() sur l’ouvert
sur l’ouvert ![]()
![]() M1. démontrer que
M1. démontrer que ![]() est différentia- ble en tout point de
est différentia- ble en tout point de ![]() et que l’application
et que l’application ![]() est continue sur
est continue sur ![]() .
.
![]() M2. introduire une base
M2. introduire une base ![]() de
de ![]() (la base canonique si
(la base canonique si ![]() ) et démontrer que
) et démontrer que ![]() admet des dérivées partielles relativement à cette base continues sur
admet des dérivées partielles relativement à cette base continues sur ![]() .
.
![]() M3. utiliser les théorèmes sur les fonctions de classe
M3. utiliser les théorèmes sur les fonctions de classe ![]() :
:
![]() combinaison linéaire de fonctions de classe
combinaison linéaire de fonctions de classe ![]() ,
,
![]() produit de deux fonctions de classe
produit de deux fonctions de classe ![]() à valeurs dans
à valeurs dans ![]() ,
,
![]() quotient de 2 fonctions de classe
quotient de 2 fonctions de classe ![]() et à valeurs dans
et à valeurs dans ![]() , le dénominateur ne s’annulant pas,
, le dénominateur ne s’annulant pas,
![]() composée de fonctions différentia- bles :
composée de fonctions différentia- bles :
hyp : ![]() est de classe
est de classe ![]() sur l’ouvert
sur l’ouvert ![]() ,
, ![]() et
et ![]() est de classe
est de classe ![]() sur l’ouvert
sur l’ouvert ![]() .
.
conclusion : ![]() est de classe
est de classe ![]() sur
sur ![]() .
.
![]() restriction à un ouvert d’une applica- tion linéaire
restriction à un ouvert d’une applica- tion linéaire ![]()
![]() cas où
cas où ![]() ,
, ![]() et
et ![]() ,
, ![]() étant bilinéaire sur
étant bilinéaire sur ![]() .
.
3.2. Utiliser des fonctions de classe ![]()
![]() Th1. Si
Th1. Si ![]() est une application de classe
est une application de classe ![]() de
de ![]() dans
dans ![]() , si
, si ![]() est une application de classe
est une application de classe ![]() de
de ![]() dans
dans ![]() , si
, si ![]() et
et ![]()
![]()
![]() Th2. Si
Th2. Si ![]() est un ouvert connexe par arcs et si
est un ouvert connexe par arcs et si ![]() est une application de classe
est une application de classe ![]() définie sur
définie sur ![]() à valeurs dans
à valeurs dans ![]() ,
,
![]() est constante sur
est constante sur ![]() ssi sa différen- tielle est nulle sur
ssi sa différen- tielle est nulle sur ![]() .
.
COURS DE MATHS
Nous avons recruté pour vous les meilleurs professeurs particuliers de maths
S'EXERCER ET APPRENDRE
Avis Google France ★★★★★ 4,8 sur 5
4. Gradient – hors extremum
4.1. Définition
![]() si
si ![]() est différentiable en
est différentiable en ![]() , le gradient de
, le gradient de ![]() en
en ![]() est l’unique vecteur noté
est l’unique vecteur noté ![]() tel que pour tout
tel que pour tout ![]() ,
, ![]() .
.
![]() Lorsque
Lorsque ![]() ,
, ![]() .
.
![]() Dans une base orthonormale
Dans une base orthonormale ![]() de
de ![]() ,
, 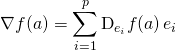 .
.
4.2. Détermination de l’orthogonal d’un sous-espace vectoriel
![]() M1. Dans le cas le plus simple :
M1. Dans le cas le plus simple : ![]() muni du produit scalaire canonique
muni du produit scalaire canonique
![]() Si
Si ![]() est l’hyperplan d’équation
est l’hyperplan d’équation ![]() dans la base canonique,
dans la base canonique, ![]() où
où ![]() .
.
![]() Soit
Soit ![]() et
et ![]() ,
, ![]() est l’hyperplan d’équation
est l’hyperplan d’équation ![]() dans la base canonique.
dans la base canonique.
![]() M2. Si
M2. Si ![]() ,
, ![]() étant une famille quelconque,
étant une famille quelconque,
![]() ssi
ssi ![]() .
.
![]() M3. Si
M3. Si ![]() est de dimension finie et si l’on connaît une base orthonormale de
est de dimension finie et si l’on connaît une base orthonormale de ![]() notée
notée ![]() ,
,
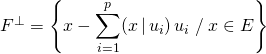 .
.
4.2. Interprétation
![]() Interprétation géométrique du gradient : si
Interprétation géométrique du gradient : si ![]() , l’ensemble
, l’ensemble ![]() admet un maximum obtenu pour
admet un maximum obtenu pour ![]() .
.
![]() Si
Si ![]() est une partie de
est une partie de ![]() et
et ![]() un point de
un point de ![]() , un vecteur
, un vecteur ![]() de
de ![]() est tangent à
est tangent à ![]() en
en ![]() s’il existe
s’il existe ![]() et un arc
et un arc ![]() défini sur
défini sur ![]() dérivable en
dérivable en ![]() à valeurs dans
à valeurs dans ![]() , tels que
, tels que![]() et
et ![]() .
.
![]() Si
Si ![]() est une fonction à valeurs réelles définie et différentiable sur un ouvert
est une fonction à valeurs réelles définie et différentiable sur un ouvert ![]() de l’espace euclidien
de l’espace euclidien ![]() , si
, si ![]() est une ligne de niveau de
est une ligne de niveau de ![]() (c’est à dire l’ensemble des
(c’est à dire l’ensemble des ![]() tels que
tels que ![]() ), alors les vecteurs tangents à
), alors les vecteurs tangents à ![]() au point
au point ![]() de
de ![]() sont orthogonaux au gradient de
sont orthogonaux au gradient de ![]() en
en ![]() .
.
![]()
![]() .
.
Plan affine tangent à une surface d’équation cartésienne ![]() en un point
en un point ![]() , lorsque
, lorsque ![]() est différentiable en
est différentiable en ![]() et
et ![]() , c’est le plan passant par
, c’est le plan passant par ![]() et orthogonal à
et orthogonal à ![]() .
.
![]()
![]() .
.
Plan affine tangent à une surface d’équation cartésienne ![]() en un point
en un point ![]() , lorsque
, lorsque ![]() est différentiable en
est différentiable en ![]() et
et ![]() , c’est le plan passant par
, c’est le plan passant par ![]() et orthogonal à
et orthogonal à ![]() .
.
Exercices sur les fonctions de plusieurs variables
1. Sont -elles de classe  ?
?
Exercice 1 : (Mines Ponts MP 2018)
On pose 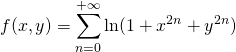 .
.
1. Déterminer le domaine de définition ![]() de
de ![]() .
.
2. ![]() est-elle de classe
est-elle de classe ![]() sur
sur ![]() ?
?
2. Fonctions à variables séparées
Exercice 2 :
1. Soit ![]() une fonction non identiquement nulle sur
une fonction non identiquement nulle sur ![]() telle que
telle que ![]() ,
, ![]() .
.
Montrer qu’il existe ![]() tel que
tel que ![]()
![]() .
.
On dit que ![]() est à variables séparées.
est à variables séparées.
2. Déterminer ![]() à variables séparées de classe
à variables séparées de classe ![]() telle que
telle que ![]() .
.
3. Déterminer ![]() de classe
de classe ![]() telle que
telle que ![]() vérifie
vérifie ![]()
![]()
![]() .
.
3. Extremums locaux
Exercice 3 :
Soit si ![]() ,
, ![]() .
.
Montrer que ![]() admet un minimum et un maximum global sur
admet un minimum et un maximum global sur ![]() et les calculer.
et les calculer.
Corrigés sur les fonctions de plusieurs variables :
Exercice 1 :
1. Soit ![]() .
.
![]() Si
Si ![]() et
et ![]() , alors
, alors ![]() avec
avec ![]() convergente comme somme de deux séries géométriques (pour
convergente comme somme de deux séries géométriques (pour ![]() et
et ![]() ), donc
), donc ![]() converge.
converge.
![]() Si
Si ![]() ou
ou ![]() ,
, ![]() , donc la suite
, donc la suite ![]() ne converge pas vers
ne converge pas vers ![]() et la série diverge grossièrement.
et la série diverge grossièrement.
En conclusion, ![]() est définie sur l’ouvert
est définie sur l’ouvert ![]() .
.
2. ![]() Existence des dérivées partielles
Existence des dérivées partielles
On fixe ![]() et on note si
et on note si ![]() et
et ![]() ,
, ![]()
![]() La série de terme général
La série de terme général ![]() converge simplement sur
converge simplement sur ![]() .
.
![]() Pour tout
Pour tout ![]() ,
, ![]() est de classe
est de classe ![]() sur
sur ![]() et
et ![]()
![]() Si
Si ![]() et si
et si ![]() ,
, ![]()
donc ![]()
et ![]() converge, donc
converge, donc ![]() converge normalement donc uniformément sur
converge normalement donc uniformément sur ![]() donc converge uniformément sur tout segment de
donc converge uniformément sur tout segment de ![]() .
.
Par le théorème de dérivation des sommes de séries de fonctions, ![]() est de classe
est de classe ![]() sur
sur ![]() et on peut dériver terme à terme.
et on peut dériver terme à terme.
On en déduit que ![]() est de classe
est de classe ![]() sur
sur ![]() lorsque
lorsque ![]() est fixé dans
est fixé dans ![]() et que si
et que si ![]()
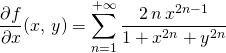 .
.
Par symétrie, si ![]() ,
,
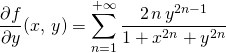 .
.
![]() Continuité de
Continuité de ![]() sur
sur ![]() .
.
On note si ![]() ,
, ![]()
![]() Pour tout
Pour tout ![]() ,
, ![]() est continue sur
est continue sur ![]() .
.
![]() Soit
Soit ![]() .
.
Pour tout ![]() ,
,![]()
donc ![]()
et ![]() converge, alors
converge, alors ![]() converge normalement sur
converge normalement sur ![]() .
.
Par le théorème de continuité des sommes de séries de fonctions, ![]() est continue sur
est continue sur ![]() .
.
Cette propriété étant vraie pour tout ![]() ,
, ![]() est continue sur
est continue sur ![]() .
.
Par symétrie, ![]() est aussi continue sur
est aussi continue sur ![]() .
.
Donc ![]() est de classe
est de classe ![]() sur
sur ![]() .
.
En Maths Spé, même si le niveau demeure élevé, certains chapitres sont plus complexes que d’autres. Il est donc important de passer un peu plus de temps sur les chapitres difficiles afin de ne pas traîner des lacunes tout au long de l’année de Maths Spé. N’hésitez pas à réviser par exemple, régulièrement ces quelques chapitres :

