Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Préhilbertiens pour les MP, PC, PSI et PT
Résumé de cours Exercices Corrigés
Résumé de cours et méthodes – Préhilbertiens
1. Pour démontrer que l’on a défini un produit scalaire
![]() M1. Si
M1. Si ![]() est un
est un ![]() -espace vectoriel,
-espace vectoriel,
![]() vérifier que
vérifier que ![]() est une forme bilinéaire symétrique en démontrant les deux propriétés :
est une forme bilinéaire symétrique en démontrant les deux propriétés :
… ![]() est linéaire
est linéaire
… et ![]() .
.
![]() puis montrer que
puis montrer que ![]() est positive non dégénérée en prouvant que :
est positive non dégénérée en prouvant que :
… ![]()
… ![]()
ce qui est plus simple en général que de prouver que : ![]() .
.
![]() M2. Lorsque
M2. Lorsque ![]() , on peut aussi
, on peut aussi
![]() écrire
écrire ![]() où
où ![]() et
et ![]() sont les matrices de
sont les matrices de ![]() et
et ![]() dans la base canonique
dans la base canonique ![]() et vérifier que
et vérifier que ![]() est une matrice symétrique réelle.
est une matrice symétrique réelle.
![]() et démontrer que
et démontrer que ![]() .
.
![]() M3. Pour montrer que
M3. Pour montrer que ![]() est une norme euclidienne, il faut montrer qu’il existe un produit scalaire
est une norme euclidienne, il faut montrer qu’il existe un produit scalaire ![]() défini sur
défini sur ![]() vérifiant
vérifiant ![]() .
.
On peut trouver l’expression de ![]() en utilisant l’une des deux identités de polarisation :
en utilisant l’une des deux identités de polarisation :
![]()
![]()
ou ![]()
![]() M4. Connaître les produits scalaires au programme.
M4. Connaître les produits scalaires au programme.
![]() Sur
Sur ![]() , le produit scalaire canonique
, le produit scalaire canonique
si ![]() et
et ![]() ,
, 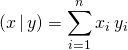 .
.
![]() Sur
Sur ![]() , le produit scalaire canonique :
, le produit scalaire canonique :
si ![]() et
et ![]()
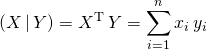 .
.
![]() Sur l’espace vectoriel
Sur l’espace vectoriel ![]() des fonctions continues sur
des fonctions continues sur ![]() à valeurs dans
à valeurs dans ![]() ,
, ![]() .
.
![]() Sur l’espace vectoriel
Sur l’espace vectoriel ![]() des fonctions continues et de carré intégrable sur l’intervalle
des fonctions continues et de carré intégrable sur l’intervalle ![]() à valeurs dans
à valeurs dans ![]() ,
, ![]() .
.
![]() et le résultat classique à savoir démontrer : Soit
et le résultat classique à savoir démontrer : Soit ![]() .
.
![]() définit un produit scalaire sur
définit un produit scalaire sur ![]() .
.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
2. Comment utiliser le fait que  est un préhilbertien réel ?
est un préhilbertien réel ?
![]() M1. Pour démontrer qu’un vecteur
M1. Pour démontrer qu’un vecteur ![]() de
de ![]() préhilbertien réel est nul, on peut
préhilbertien réel est nul, on peut
![]() démontrer que
démontrer que ![]()
![]() démontrer que
démontrer que ![]() , c’est-à-dire que
, c’est-à-dire que ![]() .
.
En particulier si l’on a prouvé que ![]() ,
,
alors ![]() , donc
, donc ![]() .
.
![]() M2. Si
M2. Si ![]() est un sous-espace vectoriel de dimension finie du préhilbertien réel
est un sous-espace vectoriel de dimension finie du préhilbertien réel ![]() ,
, ![]() .
.
![]() M3. Si
M3. Si ![]() est un préhilbertien réel, on peut utiliser l’inégalité de Cauchy-Schwarz :
est un préhilbertien réel, on peut utiliser l’inégalité de Cauchy-Schwarz :![]()
Il y a égalité si, et seulement si, la famille ![]() est liée.
est liée.
![]() M4. Inégalité de Bessel :
M4. Inégalité de Bessel :
Si ![]() est un préhilbertien réel et si
est un préhilbertien réel et si ![]() est une famille orthonormale de
est une famille orthonormale de ![]() ,
,
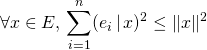 .
.
![]() M5. Cas des familles totales :
M5. Cas des familles totales :
rappel : la suite ![]() de vecteurs de
de vecteurs de ![]() est totale si l’espace vectoriel qu’elle engendre est une partie dense de
est totale si l’espace vectoriel qu’elle engendre est une partie dense de ![]() i.e.
i.e. ![]() .
.
P : Soit ![]() une suite orthonormale totale d’éléments de
une suite orthonormale totale d’éléments de ![]() .
.
On note ![]() la projection orthogonale sur l’espace
la projection orthogonale sur l’espace ![]() ,
,
![]()
soit 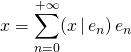 .
.
h.p : On peut démontrer la formule de Parseval :
Si ![]() est une suite orthonormale totale d’éléments de
est une suite orthonormale totale d’éléments de ![]() , alors
, alors 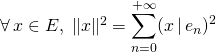 .
.
Dans la suite du paragraphe, ![]() est un espace euclidien.
est un espace euclidien.
![]() M6. Utilisation d’une base orthonormale
M6. Utilisation d’une base orthonormale ![]() ,
,
![]()
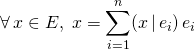 .
.
![]()
![]() ,
,
![]() et
et 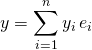 , alors
, alors 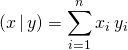 et
et 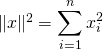 .
.
![]() Si l’on note
Si l’on note ![]() et
et ![]() les matrices colonnes de
les matrices colonnes de ![]() et
et ![]() dans la base
dans la base ![]() ,
, ![]() .
.
![]() M7. Si
M7. Si ![]() est une base orthonormale de l’espace euclidien
est une base orthonormale de l’espace euclidien ![]() et si
et si ![]() où
où ![]() ,
, ![]()
(à redémontrer).
![]() M8. Si
M8. Si ![]() est un produit scalaire sur l’espace vectoriel euclidien
est un produit scalaire sur l’espace vectoriel euclidien ![]() de base
de base ![]() , on peut définir la matrice
, on peut définir la matrice ![]() où
où ![]() ,
,
(on dit que ![]() est la matrice du produit scalaire
est la matrice du produit scalaire ![]() dans la base
dans la base ![]() ).
).
En notant ![]() et
et ![]() ,
,
![]() .
.
PROF DE MATHS PARTICULIER
Des cours de qualité et enseignants aguerris
Préparer des concours ou s'exercer
Avis Google France ★★★★★ 4,9 sur 5
3. Comment construire une famille orthonormale ?
Dans ce paragraphe, ![]() est un espace préhilbertien réel.
est un espace préhilbertien réel.
![]() M1. en utilisant le procédé d’orthonormalisation de Gram-Schmidt :
M1. en utilisant le procédé d’orthonormalisation de Gram-Schmidt :
![]() Introduire une famille libre
Introduire une famille libre ![]() de
de ![]() .
.
![]() Poser
Poser ![]() .
.
![]() Construire les vecteurs par récurrence : après avoir construit
Construire les vecteurs par récurrence : après avoir construit ![]() , on introduit la projection orthogonale
, on introduit la projection orthogonale ![]() sur
sur ![]() définie par
définie par 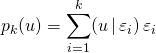 et on calcule
et on calcule ![]() puis on définit (*)
puis on définit (*) ![]() .
.
Il est aussi possible en cas d’oubli de la formule d’introduire, 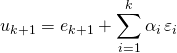
puis de chercher ![]() tels que
tels que ![]()
soit ![]() , ce qui permet de calculer les
, ce qui permet de calculer les ![]() et on termine par (*).
et on termine par (*).
Remarque : dans le cas où ![]() est de dimension finie et où
est de dimension finie et où ![]() est une base de
est une base de ![]() , on construit ainsi une base orthonormale
, on construit ainsi une base orthonormale ![]() de
de ![]() .
.
Rappel : La famille construite par le procédé d’orthonormalisation de Gram-Schmidt décrit ci-dessus est l’unique famille orthonormale vérifiant pour tout ![]() ,
, ![]() et
et
![]() .
.
![]() M2. Si
M2. Si ![]() et si
et si ![]() est de dimension finie, il suffit de construire une base orthonormale de
est de dimension finie, il suffit de construire une base orthonormale de ![]() et une base orthonormale de
et une base orthonormale de ![]() , pour obtenir une base orthonormale de
, pour obtenir une base orthonormale de ![]() par juxtaposition des bases.
par juxtaposition des bases.
![]() M3. (h.p.) Si
M3. (h.p.) Si ![]() est un espace euclidien orienté de dimension 3 et si
est un espace euclidien orienté de dimension 3 et si ![]() est une famille orthonormale,
est une famille orthonormale, ![]() est une base orthonormale directe de
est une base orthonormale directe de ![]() .
.
Pour avoir de bonnes notes et une bonne moyenne en Maths Spé, il faut connaître parfaitement son cours et également connaître les bonnes méthodes de travail à adopter. Avoir la bonne méthodologie pourra vous faire gagner beaucoup de temps et vous évitez des erreurs. Dans les cours en ligne de PT en Maths, mais aussi les cours en ligne de Maths en PC, les cours en ligne de Maths en PSI et les cours en ligne de Maths en MP mais de plus nos profs particuliers de maths comportent justement toutes les méthodes à connaître pour maximiser vos résultats.
4. Sous-espaces orthogonaux
4.1. Pour démontrer que deux sous-espaces sont orthogonaux
![]() M1. Pour démontrer que
M1. Pour démontrer que ![]() et
et ![]() sont orthogonaux, il suffit de prouver que
sont orthogonaux, il suffit de prouver que ![]() et
et ![]() ,
, ![]() .
.
![]() et
et ![]() sont orthogonaux ssi
sont orthogonaux ssi ![]() ssi
ssi ![]() .
.
![]() M2. Utilisation d’une famille génératrice.
M2. Utilisation d’une famille génératrice.
![]() Si
Si ![]() , pour montrer que
, pour montrer que ![]() et
et ![]() sont orthogonaux, il suffit de prouver que
sont orthogonaux, il suffit de prouver que ![]() .
.
![]() Si
Si ![]() et
et ![]() , pour montrer que
, pour montrer que ![]() et
et ![]() sont orthogonaux, il suffit de prouver que
sont orthogonaux, il suffit de prouver que ![]() ,
, ![]() .
.
![]() M3. Les sous-espaces propres d’un endomorphisme symétrique sont deux à deux orthogonaux.
M3. Les sous-espaces propres d’un endomorphisme symétrique sont deux à deux orthogonaux.
Si ![]() et
et ![]() sont des sous espaces orthogonaux,
sont des sous espaces orthogonaux, ![]() .
.
En effet, ![]() , alors
, alors ![]() , donc
, donc ![]() .
.
4.2. Détermination de l’orthogonal d’un sous-espace vectoriel
![]() M1. Dans le cas le plus simple :
M1. Dans le cas le plus simple : ![]() muni du produit scalaire canonique
muni du produit scalaire canonique
![]() Si
Si ![]() est l’hyperplan d’équation
est l’hyperplan d’équation ![]() dans la base canonique,
dans la base canonique, ![]() où
où ![]() .
.
![]() Soit
Soit ![]() et
et ![]() ,
, ![]() est l’hyperplan d’équation
est l’hyperplan d’équation ![]() dans la base canonique.
dans la base canonique.
![]() M2. Si
M2. Si ![]() ,
, ![]() étant une famille quelconque,
étant une famille quelconque,
![]() ssi
ssi ![]() .
.
![]() M3. Si
M3. Si ![]() est de dimension finie et si l’on connaît une base orthonormale de
est de dimension finie et si l’on connaît une base orthonormale de ![]() notée
notée ![]() ,
,
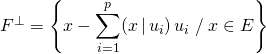 .
.
4.3. Supplémentaires orthogonaux
![]() M1. Si
M1. Si ![]() est de dimension finie ou non et si
est de dimension finie ou non et si ![]() est un sous-espace vectoriel de dimension finie de
est un sous-espace vectoriel de dimension finie de ![]() ,
, ![]() .
.
Si ![]() est de dimension infinie, il est possible lorsque
est de dimension infinie, il est possible lorsque ![]() n’est pas de dimension finie que
n’est pas de dimension finie que ![]() et
et ![]() ne soient pas des supplémentaires orthogonaux.
ne soient pas des supplémentaires orthogonaux.
![]() M2. Si
M2. Si ![]() est un préhilbertien, pour démontrer que les sous-espaces vectoriels
est un préhilbertien, pour démontrer que les sous-espaces vectoriels ![]() et
et ![]() sont des supplémentaires orthogonaux, il suffit de prouver que
sont des supplémentaires orthogonaux, il suffit de prouver que ![]() et que
et que ![]() et
et ![]()
Donc ![]() et
et ![]() .
.
![]() M3. Si
M3. Si ![]() est un espace euclidien, pour démontrer que
est un espace euclidien, pour démontrer que ![]() et
et ![]() sont des supplémentaires orthogonaux,
sont des supplémentaires orthogonaux,
![]() M3.1. la méthode la plus simple est souvent de prouver
M3.1. la méthode la plus simple est souvent de prouver ![]() et
et ![]() (a)
(a)
et de rappeler le raisonnement du 4.1. donnant : ![]() (b) donc
(b) donc ![]() , en utilisant (a) et (b).
, en utilisant (a) et (b).
![]() M3.2. Il est aussi possible de prouver que
M3.2. Il est aussi possible de prouver que ![]() et d’utiliser : dans tout espace euclidien,
et d’utiliser : dans tout espace euclidien, ![]() .
.
![]() M4. Si
M4. Si ![]() est un endomorphisme symétrique d’un espace euclidien,
est un endomorphisme symétrique d’un espace euclidien, ![]() et
et ![]() sont des supplémentaires orthogonaux.
sont des supplémentaires orthogonaux.
![]() M3.1. la méthode la plus simple est souvent de prouver
M3.1. la méthode la plus simple est souvent de prouver ![]() et
et ![]() (a)
(a)
et de rappeler le raisonnement du 4.1. donnant : ![]() (b) donc
(b) donc ![]() , en utilisant (a) et (b).
, en utilisant (a) et (b).
![]() M3.2. Il est aussi possible de prouver que
M3.2. Il est aussi possible de prouver que ![]() et d’utiliser : dans tout espace euclidien,
et d’utiliser : dans tout espace euclidien, ![]() .
.
![]() M4. Si
M4. Si ![]() est un endomorphisme symétrique d’un espace euclidien,
est un endomorphisme symétrique d’un espace euclidien, ![]() et
et ![]() sont des supplémentaires orthogonaux.
sont des supplémentaires orthogonaux.
Exercices sur les espaces préhilbertiens
1. Un problème de distance
Exercice 1 :
On note ![]() l’espace vectoriel des applications continues sur
l’espace vectoriel des applications continues sur ![]() et à valeurs réelles.
et à valeurs réelles.
1. Démontrer que l’on définit un produit scalaire sur ![]() en posant pour
en posant pour ![]() et
et ![]() dans
dans ![]() ,
, ![]() .
.
3. On note ![]() ,
, ![]() et
et ![]() . Déterminer une base orthonormale de
. Déterminer une base orthonormale de ![]() .
.
3. Déterminer le projeté orthogonal de la fonction ![]() sur le sous-espace
sur le sous-espace ![]() et en déduire la valeur du réel
et en déduire la valeur du réel ![]() .
.
2. Convergence faible et convergence
Exercice 2 :
Soit ![]() un espace préhilbertien réel. On dit qu’une suite
un espace préhilbertien réel. On dit qu’une suite ![]() de vecteurs de
de vecteurs de ![]() converge faiblement vers
converge faiblement vers ![]() si
si ![]() .
.
1. Si la suite ![]() converge vers
converge vers ![]() ,
, ![]() converge faiblement vers
converge faiblement vers ![]() .
.
2. On suppose que ![]() est de dimension finie. Si
est de dimension finie. Si ![]() converge faiblement vers
converge faiblement vers ![]() ,
, ![]() converge vers
converge vers ![]() .
.
3. La réciproque du résultat de la question 1 est fausse en dimension infinie.
3. Exercices sur les matrices de Gram
Exercice 3 :
Soit ![]() un préhilbertien réel.
un préhilbertien réel.
Étant donnés ![]() vecteurs de
vecteurs de ![]()
![]() , on définit la matrice de Gram :
, on définit la matrice de Gram :
![]() .
.
On note ![]() son déterminant.
son déterminant.
1. Si ![]() est une famille liée,
est une famille liée, ![]() .
.
2. On suppose que ![]() est libre et on note
est libre et on note ![]() .
.
Soit ![]() la matrice de la famille
la matrice de la famille ![]() dans une base orthonormale de
dans une base orthonormale de ![]() .
.
![]() et
et ![]() .
.
3. ![]() est invariant lorsque l’on ajoute à l’un des vecteurs une combinaison linéaire des autres vecteurs.
est invariant lorsque l’on ajoute à l’un des vecteurs une combinaison linéaire des autres vecteurs.
4. On suppose que ![]() est une famille libre.
est une famille libre.
Soit ![]() et
et ![]() .
.
![]() .
.
5. Soit ![]() une base orthonormale de l’espace euclidien
une base orthonormale de l’espace euclidien ![]() , et
, et ![]() .
.
![]()
Corrigés des exercices sur les préhilbertiens :
Exercice 1 :
1. ![]() Toute fonction continue sur un segment est intégrable sur ce segment, donc
Toute fonction continue sur un segment est intégrable sur ce segment, donc ![]() est défini sur
est défini sur ![]() .
.
![]() La symétrie provient de la commuta- tivité de la multiplication dans
La symétrie provient de la commuta- tivité de la multiplication dans ![]() .
.
![]() La linéarité par rapport à la première variable découle de la linéarité de l’intégrale sur le segment
La linéarité par rapport à la première variable découle de la linéarité de l’intégrale sur le segment ![]() .
.
![]() Si
Si ![]() ,
, ![]() .
.
Si ![]() ,
, ![]() est une fonction continue positive d’intégrale nulle, donc
est une fonction continue positive d’intégrale nulle, donc ![]() est nulle.
est nulle. ![]() l’est donc aussi. Ceci justifie le caractère défini positif.
l’est donc aussi. Ceci justifie le caractère défini positif.
On a prouvé que ![]() est un produit scalaire sur
est un produit scalaire sur ![]() .
.
2. On pourrait utiliser les formules de Schmidt. Cependant, il est immédiat que ![]() et il suffit de normer les vecteurs pour obtenir une base orthonormale.
et il suffit de normer les vecteurs pour obtenir une base orthonormale.
![]() et
et ![]() .
.
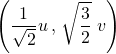 est une b.o.n. de
est une b.o.n. de ![]() .
.
3. ![]() En utilisant la base orthonormale de
En utilisant la base orthonormale de ![]() définie dans la question précédente
définie dans la question précédente 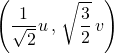 , si
, si ![]() est la projection orthogonale sur
est la projection orthogonale sur ![]() ,
,
![]() .
.
![]()
![]()
![]() .
.
![]()
![]() .
.
Donc ![]() .
.
![]() On remarque que :
On remarque que :
![]()
![]() .
.
D’après le cours, cette distance est atteinte pour ![]() et vaut donc
et vaut donc ![]() .
.
En écrivant que ![]() et en remarquant que
et en remarquant que ![]() et
et ![]() sont orthogonaux, le théorème de Pythagore donne :
sont orthogonaux, le théorème de Pythagore donne :
![]()
![Rendered by QuickLaTeX.com \Vert w\Vert ^2 =\displaystyle \left [ \frac {\textrm{e}^{2 t}} 2 \right ] _ 1 ^1 = \frac{\textrm{e}^2-\textrm{e}^{-2}}{2}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-74477479b29fd1326c2060845efcb201_l3.png) .
.
![]() .
.
![]() .
.
Un calcul au brouillon permet de simplifier cette expression et d’obtenir
![]()
![]() .
.
N’oubliez pas, avant les concours de bien revoir tous les chapitres de mathématiques au programme de Maths Spé, afin de vous assurer de n’avoir fait aucune impasse. Quelques chapitres essentiels à réviser avant les concours post-prépa :

