Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Probabilités en Maths Spé pour les MP, PC, PSI et PT
Résumé de cours Exercices Annales
Résumé de cours et méthodes – Probabilités
Plan
1. Définir une probabilité en SPE
2. Probabilité d’une réunion. (1h pour les 5 exercices)
3. Probabilité d’événements contenant l’expression « au moins » . (40 mn pour les 3 exercices)
4. Probabilité conditionnelle.(15 mn pour les 2 exercices)
5. Quelques méthodes de calcul de probabilité.(90 mn pour les 5 exercices).
6. Chaîne de Markov.
Pour les méthodes seules : 90 mn.
Toutes les probabilités obtenues doivent être éléments de ![]() .
.
Il faut s’apercevoir des erreurs flagrantes (probabilité strictement négative ou strictement supérieure à 1), reconnaître qu’il y a erreur, même si l’on ne sait pas la découvrir ou la corriger.
Les probabilités demandées seront données à ![]() en utilisant un « . » comme séparateur décimal.
en utilisant un « . » comme séparateur décimal.
1. Définir une probabilité en Maths spé
Rappel définition d’une tribu
Soit ![]() un ensemble et
un ensemble et ![]() une partie de
une partie de ![]() est une tribu sur
est une tribu sur ![]() lorsque
lorsque
![]()
![]()
![]()
![]()
![]() si
si ![]() .
.
![]() est appelé espace probabilisable.
est appelé espace probabilisable.
M1. Connaître la définition :
On suppose que ![]() est un espace probabilisable.
est un espace probabilisable. ![]() est une application de
est une application de ![]() dans
dans ![]() telle que
telle que
![]()
![]()
![]() Si
Si ![]() vérifie
vérifie ![]() , alors la série de terme général
, alors la série de terme général ![]() est convergente et
est convergente et 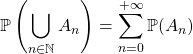 .
.
![]() est un espace probabilisé.
est un espace probabilisé.
M2. Si ![]() est un espace probabilisé,
est un espace probabilisé,
![]()
![]() .
.
![]() si
si ![]() .
.
![]() si
si ![]() , si
, si ![]() vérifie si
vérifie si ![]() ,
,
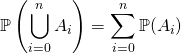 .
.
![]() si
si ![]() , si
, si ![]() ,
,
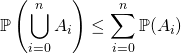 .
.
![]() si
si ![]() et
et ![]() ,
, ![]() .
.
![]() propriété de continuité croissante
propriété de continuité croissante
Si ![]() vérifie
vérifie ![]() ,
,
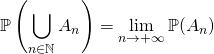 .
.
![]() propriété de continuité décroissante
propriété de continuité décroissante
Si ![]() vérifie
vérifie ![]() ,
,
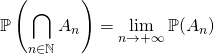 .
.
![]() si
si ![]() ,
, 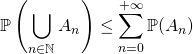
avec la convention 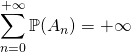 lorsque la série diverge.
lorsque la série diverge.
M3. Caractérisation d’une probabilité sur ![]() , lorsque
, lorsque ![]() est fini ou dénombrable.
est fini ou dénombrable.
Se donner une probabilité sur ![]() revient à se donner une application
revient à se donner une application ![]() telle que la famille
telle que la famille ![]() soit une famille sommable de somme égale à 1.
soit une famille sommable de somme égale à 1.
Dans ce cas, pour tout ![]()
![]() .
.
UN PROF DE MATHS POUR EXCELLER
La pratique et la compréhension
clés de la réussite
Cours de maths en ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
2. Probabilité d’une réunion
2.1. Cas d’événements deux à deux incompatibles.
Avant d’écrire 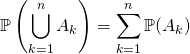 ,
,
vérifier que les événements ![]() sont deux à deux incompatibles.
sont deux à deux incompatibles.
Exercice 1 :
Soit une urne contenant une proportion ![]() de boules blanches et une proportion
de boules blanches et une proportion ![]() de boules noires avec
de boules noires avec ![]() .
.
A et B tirent alternativement chacun au plus ![]() boules avec remise et le joueur A commence. Le premier qui a tiré une boule blanche a gagné.
boules avec remise et le joueur A commence. Le premier qui a tiré une boule blanche a gagné.
Quelle est la probabilité que A gagne ? que B gagne ?
Exercice 2 :
Quelle est la probabilité d’avoir au plus un carreau en tirant 5 cartes d’un jeu de 32 cartes ?
2.2. Cas d’événements non incompatibles.
![]() Pour
Pour ![]() :
: ![]()
![]() Pour
Pour ![]() , en utilisant deux fois la formule précédente, on obtient :
, en utilisant deux fois la formule précédente, on obtient :
![]()
![]()
![]() .
.
Exercice 3
On place ![]() boules numérotées dans 4 tiroirs numérotés de 1 à 4.
boules numérotées dans 4 tiroirs numérotés de 1 à 4.
Calculer la probabilité que chacun des trois premiers tiroirs contienne au moins une boule.
Exercice 4
On place ![]() boules numérotées de
boules numérotées de ![]() à
à ![]() dans
dans ![]() tiroirs numérotés de
tiroirs numérotés de ![]() à
à ![]() , quelle est la probabilité qu’aucun tiroir ne soit vide ?
, quelle est la probabilité qu’aucun tiroir ne soit vide ?
2.3. Probabilité d’une réunion dénombrable.
Calcul de 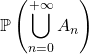 .
.
On ne sait résoudre ce problème que dans deux situations :
a) Les événements ![]() sont deux à deux incompatibles, alors
sont deux à deux incompatibles, alors 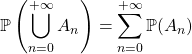 .
.
b) La suite ![]() est une suite croissante d’événements (
est une suite croissante d’événements (![]() ), alors
), alors 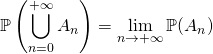 . (propriété de continuité croissante)
. (propriété de continuité croissante)
Exercice 5
Démontrer que si pour tout entier ![]() ,
, ![]() est un événement négligeable (de probabilité nulle), leur réunion est négligeable.
est un événement négligeable (de probabilité nulle), leur réunion est négligeable.
3. Probabilité d’événements contenant l’expression « au moins »
3.1. Calcul de  où
où  est l’événement « avoir au moins un élément vérifiant une propriété
est l’événement « avoir au moins un élément vérifiant une propriété  «
«
![]() M1 : on passe par le complémentaire
M1 : on passe par le complémentaire ![]() est l’événement « n’avoir aucun élément vérifiant
est l’événement « n’avoir aucun élément vérifiant ![]() « .
« .
![]() M2 : on peut aussi poser
M2 : on peut aussi poser 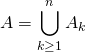 où
où ![]() est l’événement « avoir exactement
est l’événement « avoir exactement ![]() éléments vérifiant
éléments vérifiant ![]() » en cherchant le nombre maximum
» en cherchant le nombre maximum ![]() d’éléments vérifiant
d’éléments vérifiant ![]() que l’on peut obtenir ; les événements
que l’on peut obtenir ; les événements ![]() étant deux à deux disjoints,
étant deux à deux disjoints, 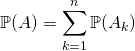 .
.
![]() M3 : on peut aussi se ramener au calcul de
M3 : on peut aussi se ramener au calcul de 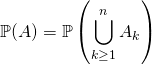 où les
où les ![]() ne sont pas deux à deux disjoints.
ne sont pas deux à deux disjoints.
Exercice 1
En tirant 6 cartes dans un jeu de 32 cartes, probabilité d’avoir au moins une paire de coeurs.
3.2. Calcul de  où
où  : « avoir au moins un élément vérifiant une propriété
: « avoir au moins un élément vérifiant une propriété  » et
» et  : « avoir
: « avoir  éléments vérifiant une propriété
éléments vérifiant une propriété  «
«
Si ![]() est l’univers, on utilise
est l’univers, on utilise ![]() , alors
, alors
![]() ,
,
les événements étant incompatibles, ![]() .
.
Donc ![]() .
.
Exercice 2
En tirant 5 cartes dans un jeu de 32 cartes, quelle est la probabilité d’avoir deux valets et au moins un as ?
3.3. Calcul de  où
où  : « avoir au moins un élément vérifiant une propriété
: « avoir au moins un élément vérifiant une propriété  » et
» et  : « avoir au moins un élément vérifiant une propriété
: « avoir au moins un élément vérifiant une propriété  «
«
On passe par le complémentaire ![]() .
.
En général ![]() et
et ![]() ne sont pas incompatibles.
ne sont pas incompatibles.
Exercice 3
En tirant 5 cartes dans un jeu de 32 cartes, quelle est la probabilité d’avoir au moins un as et au moins un cœur ?
4. Probabilité conditionnelle
4.1. Il faut distinguer les quantités  et
et 
a) Quand on calcule ![]() , on calcule la probabilité que
, on calcule la probabilité que ![]() et
et ![]() soient réalisés en même temps.
soient réalisés en même temps.
Dans ce cas, ![]() est un événement
est un événement
b) Quand on calcule ![]() , on calcule un quotient de probabilités :
, on calcule un quotient de probabilités : ![]() .
.
![]() n’est pas un événement.
n’est pas un événement.
On sait que ![]() est réalisé et on cherche la probabilité que
est réalisé et on cherche la probabilité que ![]() soit réalisé lorsque
soit réalisé lorsque ![]() l’est.
l’est.
Cela nécessite une lecture attentive de l’énoncé.
![]() Dans certains cas, il est évident que l’on demande une probabilité conditionnelle, car on demande la probabilité d’un événement sachant (ou lorsque) l’on a obtenu
Dans certains cas, il est évident que l’on demande une probabilité conditionnelle, car on demande la probabilité d’un événement sachant (ou lorsque) l’on a obtenu ![]() . On peut repérer cette situation en cherchant les mots « sachant », « si », « lorsque » dans l’énoncé.
. On peut repérer cette situation en cherchant les mots « sachant », « si », « lorsque » dans l’énoncé.
![]() Dans d’autres cas, on donne la réalisation de l’événement
Dans d’autres cas, on donne la réalisation de l’événement ![]() , dans une phrase du type « on a obtenu ? » et on demande ensuite de calculer la probabilité de
, dans une phrase du type « on a obtenu ? » et on demande ensuite de calculer la probabilité de ![]() , donc de calculer
, donc de calculer ![]() .
.
![]() Par contre, si l’on demande le calcul de
Par contre, si l’on demande le calcul de ![]() , il faut voir s’il vaut mieux calculer :
, il faut voir s’il vaut mieux calculer :
![]()
![]() : événements de « mêmes rangs » ou de « même époque ».
: événements de « mêmes rangs » ou de « même époque ».
![]()
![]() c’est-à-dire si la réalisation de
c’est-à-dire si la réalisation de ![]() permet de savoir comment réaliser
permet de savoir comment réaliser ![]() .
.
On rappelle que si ![]() vérifie
vérifie ![]() ,
, ![]() définit une probabilité sur
définit une probabilité sur ![]() .
.
4.2. Utilisation de la formule des probabilités composées
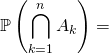
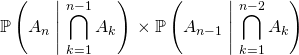
![]() .
.
Ne pas oublier de vérifier que ![]() , pour justifier l’existence des probabilités conditionnelles.
, pour justifier l’existence des probabilités conditionnelles.
On conditionne « en remontant le temps », c’est-à-dire par les événements antérieurs.
4.3. Probabilité d’une intersection dénombrable
On ne sait calculer 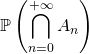 que lorsque
que lorsque ![]() : par propriété de continuité décroissante,
: par propriété de continuité décroissante,
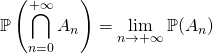 .
.
Exercice 1
Si l’on effectue des tirages avec remise dans une urne contenant une proportion ![]() de boules rouges, calculer la probabilité de toujours obtenir une boule bouge.
de boules rouges, calculer la probabilité de toujours obtenir une boule bouge.
Exercice 2
Soit ![]() une suite d’événements mutuellement indépendants.
une suite d’événements mutuellement indépendants.
On note 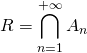 .
.
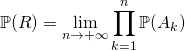 .
.
COURS DE MATHS
Nous avons recruté pour vous les meilleurs professeurs particuliers de maths
S'EXERCER ET APPRENDRE
Avis Google France ★★★★★ 4,8 sur 5
5. Quelques méthodes de calcul de probabilité
5.1. Utilisation de la formule des probabilités totales
![]() Rappel de la formule
Rappel de la formule
Soit ![]() un espace probabilisé.
un espace probabilisé.
![]() Si
Si ![]() est un système complet d’événements de probabilité non nulle, pour tout
est un système complet d’événements de probabilité non nulle, pour tout ![]() ,
, 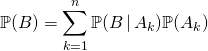 .
.
![]() Si
Si ![]() est un système complet (ou quasi-complet) d’événements, pour tout
est un système complet (ou quasi-complet) d’événements, pour tout ![]() ,
, 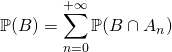
Ce que l’on peut écrire sous la forme
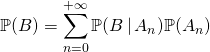 ,
,
…. si pour tout ![]() ,
, ![]()
…. en ajoutant la convention si ![]() ,
, ![]() .
.
![]() M1 Lorsque l’on fait des tirages qui peuvent avoir lieu dans des urnes différentes ou dans des conditions différentes qui sont définies par les résultats d’une première épreuve, il faut introduire un système complet d’événements correspondant aux différents choix des urnes ou des différents résultats de la première épreuve.
M1 Lorsque l’on fait des tirages qui peuvent avoir lieu dans des urnes différentes ou dans des conditions différentes qui sont définies par les résultats d’une première épreuve, il faut introduire un système complet d’événements correspondant aux différents choix des urnes ou des différents résultats de la première épreuve.
Exercice 1
On lance un dé équilibré. Lorsque l’on obtient la face ![]() , on tire dans une urne contenant les jetons numérotés de 1 à
, on tire dans une urne contenant les jetons numérotés de 1 à ![]() . Quelle est la probabilité d’obtenir un jeton numéroté 1 ?
. Quelle est la probabilité d’obtenir un jeton numéroté 1 ?
![]() M2 Lorsque les résultats de l’épreuve
M2 Lorsque les résultats de l’épreuve ![]() dépendent des résultats de l’épreuve
dépendent des résultats de l’épreuve ![]() , introduire un système complet d’événements correspondant à toutes les éventualités du rang
, introduire un système complet d’événements correspondant à toutes les éventualités du rang ![]() et utiliser la formule des probabilités totales.
et utiliser la formule des probabilités totales.
Exercice 2
On a deux urnes contenant respectivement une proposition ![]() et
et ![]() de boules blanches. Le premier tirage a lieu dans la première urne.
de boules blanches. Le premier tirage a lieu dans la première urne.
Puis si l’on obtient une boule blanche, le tirage suivant se fait dans l’urne 1 sinon il se fait dans l’urne 2.
Si ![]() est la probabilité d’obtenir une boule blanche au
est la probabilité d’obtenir une boule blanche au ![]() -ème tirage, trouver une relation de récurrence liant
-ème tirage, trouver une relation de récurrence liant ![]() et
et ![]() .
.
![]() M3 Lorsque les résultats de l’épreuve
M3 Lorsque les résultats de l’épreuve ![]() dépendent des résultats de toutes les épreuves précédentes, introduire un système complet d’événements correspondant à toutes les éventualités des premières épreuves permettant soit de terminer l’ensemble des épreuves soit de « remettre le compteur à zéro » et utiliser la formule des probabilités totales.
dépendent des résultats de toutes les épreuves précédentes, introduire un système complet d’événements correspondant à toutes les éventualités des premières épreuves permettant soit de terminer l’ensemble des épreuves soit de « remettre le compteur à zéro » et utiliser la formule des probabilités totales.
Si ![]() est un des événements du système complet précédent correspondant à
est un des événements du système complet précédent correspondant à ![]() épreuves, on sera donc amené à calculer des probabilités du type
épreuves, on sera donc amené à calculer des probabilités du type ![]() : il reste
: il reste ![]() épreuves à effectuer pour passer d’une situation résultant de la réalisation de
épreuves à effectuer pour passer d’une situation résultant de la réalisation de ![]() à une situation où l’on doit avoir
à une situation où l’on doit avoir ![]() .
.
Exercice 3
On joue à pile (probabilité ![]() ) ou face (probabilité
) ou face (probabilité ![]() ) en arrêtant dès que l’on obtient pour la première fois deux piles de suite.
) en arrêtant dès que l’on obtient pour la première fois deux piles de suite.
On note ![]() la probabilité de s’arrêter au
la probabilité de s’arrêter au ![]() -ème lancer.
-ème lancer.
Trouver une relation de récurrence exprimant ![]() en fonction des
en fonction des ![]() si
si ![]() .
.
On peut calculer la probabilité que le jeu s’arrête au bout d’un nombre fini d’épreuves sans avoir calculé ![]() .
.
![]() M4 Dans une suite infinie d’épreuves, lorsque l’on gagne en obtenant pour la première fois une suite donnée de résultats, pour calculer la probabilité de gagner, on peut introduire un système complet d’événements correspondant aux premières épreuves (on obtient la bonne figure, ou on revient après quelques épreuves « à une remise à zéro »).
M4 Dans une suite infinie d’épreuves, lorsque l’on gagne en obtenant pour la première fois une suite donnée de résultats, pour calculer la probabilité de gagner, on peut introduire un système complet d’événements correspondant aux premières épreuves (on obtient la bonne figure, ou on revient après quelques épreuves « à une remise à zéro »).
Exercice 4
Dans une suite d’épreuves indépendantes de pile (probabilité ![]() ) et face (probabilité
) et face (probabilité ![]() ), on gagne en obtenant la suite
), on gagne en obtenant la suite ![]() .
.
Quelle est la probabilité de gagner ?
5.2. Calcul de  où
où  est du type « il faut faire
est du type « il faut faire  épreuves pour obtenir un
épreuves pour obtenir un  -ème élément vérifiant
-ème élément vérifiant  « (avec
« (avec  et
et  ).
).
On écrit ![]() avec
avec
![]()
![]() : « lors de la
: « lors de la ![]() ème épreuve, on obtient un élément vérifiant
ème épreuve, on obtient un élément vérifiant ![]() »
»
![]()
![]() : « lors des
: « lors des ![]() premières épreuves, on a obtenu
premières épreuves, on a obtenu ![]() éléments vérifiant
éléments vérifiant ![]() et
et ![]() éléments ne vérifiant pas
éléments ne vérifiant pas ![]() « .
« .
puis on utilise ![]() .
.
Exercice 5
On lance une pièce donnant pile avec la probabilité ![]() jusqu’à obtenir le troisième pile.
jusqu’à obtenir le troisième pile.
Quelle est la probabilité de lancer la pièce ![]() fois (avec
fois (avec ![]() ) ?
) ?
5.3. Recherche de la probabilité de gain de  dans une suite de jeux
dans une suite de jeux
a) On note ![]() l’événement «
l’événement « ![]() gagne la partie avec le
gagne la partie avec le ![]() -ième jeu » .
-ième jeu » .
On cherche ![]() l’ensemble des numéros des jeux où
l’ensemble des numéros des jeux où ![]() peut gagner (attention
peut gagner (attention ![]() peut être infini si l’on a une suite infinie de jeux).
peut être infini si l’on a une suite infinie de jeux).
Si ![]() est l’événement «
est l’événement « ![]() gagne »,
gagne », ![]() et
et ![]()
b) Si l’unique adversaire de ![]() est
est ![]() , il est possible que la probabilité que
, il est possible que la probabilité que ![]() gagne ne soit pas égale à
gagne ne soit pas égale à ![]() : il existe des jeux où il n’y a pas de gagnant.
: il existe des jeux où il n’y a pas de gagnant.
En reprenant l’exemple du paragraphe 1.1., la probabilité qu’il y ait un gagnant est ![]() .
.
6. Chaîne de Markov
On considère une suite d’épreuves identiques, chaque épreuve pouvant donner ![]() résultats différents.
résultats différents.
On note les ![]() résultats à l’épreuve
résultats à l’épreuve ![]() sous la forme
sous la forme ![]() .
.
Méthode habituelle dans les sujets :
On suppose que, pour tout ![]() et pour tout
et pour tout ![]() , la probabilité
, la probabilité ![]() ne dépend pas de
ne dépend pas de ![]() et on la note
et on la note ![]() .
.
On introduit la matrice ![]()
On définit la matrice colonne ![]() de type
de type ![]() par
par ![]() .
.
Par la formule des probabilités totales, 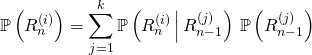 ce qui se traduit matriciellement par
ce qui se traduit matriciellement par ![]() .
.
On en déduit ![]() par la formule
par la formule ![]() ou
ou ![]() . Il suffit de savoir diagonaliser
. Il suffit de savoir diagonaliser ![]() pour trouver
pour trouver ![]() .
.
Quelques remarques utiles :
R1 : La somme des termes de chaque colonne de ![]() est égale à 1.
est égale à 1.
R2 : La matrice ![]() est dite stochastique : les coefficients de
est dite stochastique : les coefficients de ![]() sont positifs ou nuls et la somme des termes de chaque ligne de
sont positifs ou nuls et la somme des termes de chaque ligne de ![]() est égale à 1.
est égale à 1.
1 est valeur propre de ![]() (donc aussi de
(donc aussi de ![]() ), la matrice colonne dont tous les termes sont égaux à 1 est un vecteur propre de
), la matrice colonne dont tous les termes sont égaux à 1 est un vecteur propre de ![]() associé à la valeur propre 1.
associé à la valeur propre 1.
et deux résultats que l’on trouve dans de nombreux sujets :
Théorème3 : On peut démontrer que les valeurs propres de ![]() (donc de
(donc de ![]() ) sont de module inférieur ou égal à 1.
) sont de module inférieur ou égal à 1.
Théorème4 : Si les éléments de la matrice ![]() sont strictement positifs, 1 est la seule valeur propre de module 1 de
sont strictement positifs, 1 est la seule valeur propre de module 1 de ![]() et le sous-espace propre associé à la valeur propre 1 est de dimension 1.
et le sous-espace propre associé à la valeur propre 1 est de dimension 1.
Pour les exercices demandant de prouver que pour tout ![]() , la suite
, la suite ![]() converge :
converge :
a) Étudier la réduction de ![]() .
.
Lorsque ![]() est diagonalisable dans
est diagonalisable dans ![]() , il existe
, il existe ![]() telle que
telle que ![]() , où
, où ![]() .
.
b) ![]() . On suppose dans la suite que
. On suppose dans la suite que ![]() est tel que
est tel que ![]()
![]()
Dans ce cas,![]() (
(![]() fois 1 et
fois 1 et ![]() fois 0).
fois 0).
Par continuité de l’endomorphisme de ![]() ,
, ![]() ,
, ![]() .
.
La suite ![]() converge vers
converge vers ![]() .
.
c) Par continuité de l’application linéaire ![]() ,
, ![]() ,
,
![]() que l’on note
que l’on note ![]() .
.
d) ![]() , par continuité de l’endomorphisme de
, par continuité de l’endomorphisme de ![]() ,
, ![]() , on obtient :
, on obtient : ![]() .
.
e) Si ![]() ,
, 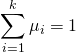 .
.
avec pour tout ![]()
car pour tout ![]() ,
,
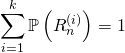 et
et ![]() .
.
f) Lorsque ![]() , le sous espace propre de
, le sous espace propre de ![]() associé à la valeur propre 1 est de dimension 1,
associé à la valeur propre 1 est de dimension 1, ![]() est le vecteur propre de
est le vecteur propre de ![]() associé à la valeur propre 1 et dont la somme des coefficients est égale à 1.
associé à la valeur propre 1 et dont la somme des coefficients est égale à 1.
Autre traduction :
Certains énoncés peuvent introduire la matrice ligne de type ![]() .
.
![]() .
.
Dans ce cas, on note ![]() avec
avec ![]() .
.
Alors, ![]() où
où ![]() est définie ci-dessus.
est définie ci-dessus.
La relation s’écrit ![]() .
.
Les cours en prépa se déroulent relativement rapidement et certaines notions importantes sont parfois abordées trop vite. Les cours en ligne de Maths en PSI, les cours en ligne de Maths en MP et les cours en ligne de Maths en PC ou aussi les cours en ligne de Maths en PT permettent ainsi aux étudiants de pouvoir compléter leur prise de notes.
Exercices sur les probabilités en maths spé
Plan
1. Ajout de boules après tirages (30 mn).
2. Balade sur un triangle (20 mn).
3. Des questions de parité (20 mn).
4. Un jeu de fléchette (20 mn).
5. Tirages de parties de ![]() (60 mn)
(60 mn)
6. ![]() boules pour
boules pour ![]() boîtes (30 mn)
boîtes (30 mn)
1. Ajout de boules après tirage
Soit une urne contenant initialement ![]() boules blanches et
boules blanches et ![]() boules rouges. On note
boules rouges. On note ![]() .
.
À la suite de chaque tirage, on remet dans l’urne la boule tirée ainsi que ![]() boules de la même couleur (
boules de la même couleur (![]() ).
).
Question 1
Quelle est la probabilité en ![]() tirages de n’obtenir que des blanches ?
tirages de n’obtenir que des blanches ?
Question 2
La probabilité d’obtenir une boule blanche au deuxième tirage si l’on a obtenu blanc au premier et troisième tirage est égale à
a) ![]() b)
b) ![]() c)
c) ![]() .
.
Question 3
La probabilité de tirer blanc au ![]() -ième tirage ne dépend pas de
-ième tirage ne dépend pas de ![]() .
.
2. Balade sur un triangle
CCP MP 2018
Une puce se déplace sur un triangle équilatéral ![]() .
.
Elle se situe initialement en ![]() .
.
Si elle est en ![]() à un instant
à un instant ![]() donné, elle se déplace sur un des deux autres sommets à l’instant
donné, elle se déplace sur un des deux autres sommets à l’instant ![]() de manière équiprobable.
de manière équiprobable.
Si elle est en ![]() à un instant
à un instant ![]() donné, elle se déplace sur un des deux autres sommets à l’instant
donné, elle se déplace sur un des deux autres sommets à l’instant ![]() de manière équiprobable.
de manière équiprobable.
Si elle est en ![]() à un instant, elle reste en
à un instant, elle reste en ![]() à l’instant suivant.
à l’instant suivant.
On note ![]() (resp
(resp ![]() ) « La puce est en
) « La puce est en ![]() (resp
(resp ![]() ) à l’instant
) à l’instant ![]() « .
« .
On note ![]() (resp
(resp ![]() ,
, ![]() )
) ![]() (resp
(resp ![]() ,
, ![]() ).
).
Question 1
a) Déterminer ![]() en fonction de
en fonction de ![]() .
.
b) Soit 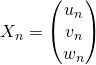 . Il existe une matrice
. Il existe une matrice ![]() telle que
telle que ![]() .
.
Question 2
Donner les expressions explicites de ![]() .
.
Question 3
Que se passe-t-il lorsque ![]() ? Expliquer.
? Expliquer.
3. Des questions de parité
TPE MP 2018
On dispose de ![]() pièces numérotées. La
pièces numérotées. La ![]() -ième pièce a une probabilité égale à
-ième pièce a une probabilité égale à ![]() de donner pile.
de donner pile.
Question 1
On note ![]() la probabilité d’avoir un nombre pair de « pile » après avoir lancé les
la probabilité d’avoir un nombre pair de « pile » après avoir lancé les ![]() premières pièces. Exprimer
premières pièces. Exprimer ![]() en fonction de
en fonction de ![]() et
et ![]() .
.
Question 2
Quelle est la probabilité d’avoir un nombre pair de « pile » en lançant toutes les pièces ?
4. Un jeu de fléchettes
A, B et C jouent aux fléchettes.
La probabilité que A (resp. B, resp. C) touche la cible est égale à ![]() (resp.
(resp. ![]() , resp
, resp ![]() ).
).
On choisit au hasard le premier joueur.
Question 1
Quelle est la probabilité que la cible soit atteinte ?
Question 2
Si la cible n’est pas atteinte, A rejoue. Quelle est la probabilité que A touche la cible ?
Question 3.
La cible a été touchée. Quelle est la probabilité que ce soit par A ?
5. Tirages de parties de 
Soient ![]() et
et ![]() un ensemble de cardinal
un ensemble de cardinal ![]() .
.
Partie 1
On se donne une partie ![]() de
de ![]() , de cardinal
, de cardinal ![]() où
où ![]() .
.
On tire au hasard une partie ![]() de
de ![]() .
.
On suppose que toutes les parties de ![]() ont la même probabilité d’être tirées.
ont la même probabilité d’être tirées.
Question 1
Calculer la probabilité de tirer la partie ![]() .
.
Question 2
Calculer la probabilité de l’événement ![]() : « la partie tirée contient
: « la partie tirée contient ![]() « .
« .
Question 3
On note ![]() l’événement « la partie tirée est incluse dans
l’événement « la partie tirée est incluse dans ![]() « . Les événements
« . Les événements ![]() et
et ![]() sont-ils indépendants ?
sont-ils indépendants ?
Question 4
Calculer la probabilité de tirer une partie disjointe de ![]() .
.
Deuxième partie
On tire maintenant avec remise deux parties de ![]() .
.
Question 1
Quelle est la probabilité qu’elles soient égales ?
Question 2
Quelle est la probabilité qu’elles soient disjointes ?
Question 3
Quelle est la probabilité que l’une des parties tirées soit incluse dans l’autre ?
Question 4
On se donne une partie ![]() de
de ![]() à
à ![]() éléments (
éléments (![]() ).
).
Quelle est la probabilité que l’intersection des deux parties tirées soit égale à ![]() ?
?
Question 5 (plus simple en utilisant des variables aléatoires)
Quelle est la probabilité que les parties tirées aient même cardinal ?
6.  boules pour
boules pour  boîtes
boîtes
Un sac contient ![]() boules noires et
boules noires et ![]() boules blanches, discernables (
boules blanches, discernables (![]() ).
).
On répartit au hasard ces boules dans ![]() boîtes, à raison de deux boules par boîte.
boîtes, à raison de deux boules par boîte.
Question 1
Calculer la probabilité ![]() pour que chaque boîte contienne une boule de chaque couleur.
pour que chaque boîte contienne une boule de chaque couleur.
Question 2
Calculer la probabilité ![]() pour que chaque boîte contienne deux boules de la même couleur.
pour que chaque boîte contienne deux boules de la même couleur.
Question 3
Montrer que pour tout ![]()
![]()
Question 4
Déterminer ![]() et
et ![]()
Autres exercices
Plan
1. Une tribu et une probabilité (15 mn)
2. Probabilité sur ![]() (20 mn)
(20 mn)
3. Un jeu de balle (30 mn).
4. Une inégalité (30 mn).
5. Remplir trois boîtes (45 mn).
6. Suite croissante de résultats (30 mn).
7. Lemme de Borel Cantelli (40 mn).
8. Probabilités et nombres premiers (40 mn).
9. Un jeu de pile ou face (60 mn).
10. Démonstration de la formule de Poincaré en utilisant des variables aléatoires. (30 mn).
1. Une tribu et une probabilité
Question 1
Soit ![]() un ensemble infini non dénombrable.
un ensemble infini non dénombrable.
On note ![]() l’ensemble des parties
l’ensemble des parties ![]() de
de ![]() telles que
telles que ![]() ou
ou ![]() est fini ou dénombrable.
est fini ou dénombrable.
![]() est une tribu sur
est une tribu sur ![]() .
.
Question 2
On définit la fonction ![]() sur
sur ![]() par si
par si ![]() ,
, ![]() si
si ![]() est fini ou dénombrable et
est fini ou dénombrable et ![]() si
si ![]() n’est pas fini ou dénombrable.
n’est pas fini ou dénombrable.
![]() est une probabilité sur
est une probabilité sur ![]() .
.
2. Une probabilité sur 
Question 1
Déterminer le réel ![]() qu’il existe une probabilité sur
qu’il existe une probabilité sur ![]() telle que si
telle que si ![]()
Question 2
Soit ![]() , on note
, on note ![]() l’événement : » l’entier tiré est un multiple de
l’événement : » l’entier tiré est un multiple de ![]() « . Calculer
« . Calculer ![]() .
.
Question 3
Calculer ![]() .
.
Question 4
On note ![]() l’événement » l’entier tiré est un nombre premier ».
l’événement » l’entier tiré est un nombre premier ».
![]()
3. Un jeu de balle
Trois enfants A, B et C jouent avec une balle.
Lorsque A a la balle, la probabilité pour qu’il l’envoie à B est 0.75 et la probabilité pour qu’il l’envoie à C est 0.25.
Lorsque B a la balle, la probabilité pour qu’ il l’envoie à A est 0.75 et la probabilité pour qu’il l’envoie à C est 0.25.
C envoie toujours la balle à B.
On désigne respectivement par ![]() ,
, ![]() et
et ![]() les probabilités pour qu’à l’issue du jeu
les probabilités pour qu’à l’issue du jeu ![]() ce soit A, resp B, resp. C qui ait la balle.
ce soit A, resp B, resp. C qui ait la balle.
Question 1
Montrer qu’il existe une matrice carrée d’ordre 3 notée ![]() telle que
telle que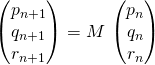 .
.
Question 2
Exprimer la matrice ![]() sous forme de produit de matrices simples.
sous forme de produit de matrices simples.
Question 3
Démontrer que les suites ![]() et
et ![]() convergent et en déterminer les limites.
convergent et en déterminer les limites.
On vérifiera que ces limites sont indépendantes de l’enfant qui avait la balle au début du jeu.
4. Une inégalité
CCP MP 2018
Soit ![]() un espace probabilisé.
un espace probabilisé.
Question 1
Si ![]() , l’inégalité
, l’inégalité ![]() est vérifiée.
est vérifiée.
Question 2
Soient ![]() deux éléments de
deux éléments de ![]() , incompatibles.
, incompatibles.
![]() .
.
Question 3
Soient ![]() deux éléments de
deux éléments de ![]() .
.
a) Montrer que
![]()
![]()
b) Montrer que ![]() .
.
Question 4
L’inégalité précédente est une égalité si, et seulement si,
![]()
![]() .
.
5. Remplir trois boîtes
Des boules indiscernables en nombre infini sont placées dans des boites numérotées de 1 à 3 à capacité illimitée.
On place les boules indépendamment les unes des autres.
On arrête quand les trois boîtes sont non vides.
Question 1
On note ![]() l’événement « on a placé
l’événement « on a placé ![]() boules lorsque pour la première fois deux boîtes des trois boîtes sont non vides ».
boules lorsque pour la première fois deux boîtes des trois boîtes sont non vides ».
Calculer ![]() .
.
Question 2
![]() est un système quasi-complet d’événements.
est un système quasi-complet d’événements.
Question 3
On note ![]() l’événement « on a placé
l’événement « on a placé ![]() boules lorsque pour la première fois les trois boîtes sont non vides ».
boules lorsque pour la première fois les trois boîtes sont non vides ».
Si ![]() ,
, ![]() ,
, ![]() est égal à
est égal à
a) ![]() b)
b)![]() c)
c)![]()
Question 4
La probabilité d’arrêter la répartition au bout d’un nombre fini d’épreuves est égale à 1
Question 5
Quelle est la probabilité d’arrêter avec deux boîtes ne contenant qu’une seule boule ?
6. Suite croissante de résultats
Question 1
Soit ![]() et
et ![]() deux entiers naturels non nuls. On note
deux entiers naturels non nuls. On note ![]()
![]() .
.
En utilisant ![]() définie sur
définie sur ![]() par
par ![]() où
où ![]() ,
,
déterminer ![]() .
.
Dans la suite, ![]() . On effectue des tirages avec remise dans un sac contenant
. On effectue des tirages avec remise dans un sac contenant ![]() jetons numérotés de
jetons numérotés de ![]() à
à ![]() .
.
Question 2.
Si ![]() , on note
, on note ![]() l’événement : « les
l’événement : « les ![]() numéros tirés sont rangés par ordre croissant (au sens large) ».
numéros tirés sont rangés par ordre croissant (au sens large) ».
Calculer ![]() .
.
On pose ![]() .
.
Question 3
En utilisant la série de terme général ![]() , déterminer la convergence de la suite
, déterminer la convergence de la suite ![]() et sa limite.
et sa limite.
Question 4
On arrête les tirages lorsque l’on obtient pour la première fois un numéro strictement inférieur aux numéros déjà tirés.
La probabilité d’obtenir d’arrêter au bout d’un nombre fini de tirages est strictement inférieure à 1.
Question 5
Quelle est la probabilité ![]() d’arrêter au
d’arrêter au ![]() -ième tirage ?
-ième tirage ?
7. Lemme de Borel-Cantelli
Soit ![]() une suite d’événements de l’espace probabilisé
une suite d’événements de l’espace probabilisé ![]() ,
,
Question 1
On note ![]() : « une infinité d’événements
: « une infinité d’événements ![]() sont réalisés ».
sont réalisés ».
Exprimer ![]() et justifier que
et justifier que ![]() est un événement.
est un événement.
Question 2
On suppose que ![]() est convergente.
est convergente. ![]() est un événement
est un événement
Question 3
On suppose que les événements ![]() sont indépendants et que
sont indépendants et que ![]() diverge.
diverge. ![]() est un événement
est un événement
Question 4 application :
Soit une épreuve ayant ![]() issues distinctes équiprobables.
issues distinctes équiprobables.
Soit ![]() et
et ![]() l’événement « au cours des
l’événement « au cours des ![]() premières épreuves, on obtient chacun des
premières épreuves, on obtient chacun des ![]() résultats
résultats ![]() fois « . On dit alors qu’il y a compensation exacte.
fois « . On dit alors qu’il y a compensation exacte.
a) Calculer ![]() .
.
b) En déduire un équivalent de ![]() .
.
c) Si ![]() , l’événement « il n’y a qu’un nombre fini de compensations exactes » est
, l’événement « il n’y a qu’un nombre fini de compensations exactes » est
8. Probabilités et nombres premiers
On note si 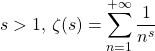 .
.
Question 1
Déterminer le réel ![]() tel qu’il existe une probabilité
tel qu’il existe une probabilité ![]() sur
sur ![]() telle que
telle que ![]() .
.
Question 2
Soit ![]() et
et ![]() l’ensemble des éléments de
l’ensemble des éléments de ![]() divisibles par
divisibles par ![]() . Calculer
. Calculer ![]() .
.
Question 3
On note ![]() l’ensemble des nombres premiers.
l’ensemble des nombres premiers.
Si ![]() on note
on note ![]() l’ensemble des éléments de
l’ensemble des éléments de ![]() divisibles par
divisibles par ![]() .
.
![]() est une famille d’événements mutuellement indépendants.
est une famille d’événements mutuellement indépendants.
Question 4
En déduire que 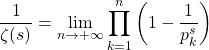 .
.
9. Un jeu de pile ou face
On effectue une série de lancers d’une pièce donnant pile avec une probabilité ![]() et face avec la probabilité
et face avec la probabilité ![]() .
.
Le joueur A gagne si « PFP » sort avant « FFP » auquel cas B gagne.
On note ![]() : « face sort au
: « face sort au ![]() -ième jeu » et
-ième jeu » et ![]() : « pile sort au
: « pile sort au ![]() -ième jeu »,
-ième jeu »,
![]() : « A gagne » et
: « A gagne » et ![]() : « B gagne ».
: « B gagne ».
Question 1
La probabilité de n’obtenir que des faces à partir du rang 2 est nulle
Question 2
Calculer ![]() en fonction de
en fonction de ![]() . En déduire
. En déduire ![]() .
.
Question 3
Calculer ![]() et
et ![]() . En déduire
. En déduire ![]() .
.
Question 4
« Il y a un gagnant » est un événement presque certain
10. Démonstration de la formule de Poincaré ou du crible
Soit ![]() un espace probabilisé.
un espace probabilisé.
Si ![]() est une partie de
est une partie de ![]() , on appelle fonction caractéristique de
, on appelle fonction caractéristique de ![]() la fonction
la fonction ![]() définie sur
définie sur ![]() à valeurs dans
à valeurs dans ![]() par
par
![]() si
si ![]() et
et ![]() si
si ![]() .
.
Question 1
![]() est une variable aléatoire sur
est une variable aléatoire sur ![]() ssi
ssi ![]() .
.
Question 2
Soient ![]() .
.
a) Déterminer ![]() ,
, ![]() .
.
b) ![]() .
.
Question 3
Soit ![]() .
.
En utilisant le développement de 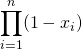 où
où ![]() et les fonctions caractéristiques des événements
et les fonctions caractéristiques des événements ![]() , démontrer la formule du crible ou Poincaré :
, démontrer la formule du crible ou Poincaré :
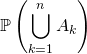
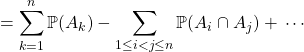
![]()
![]() .
.
Annales sur les probabilités en maths spé
Toutes les annales sont disponibles gratuitement dans la rubrique Annales.
L’intégralité des chapitres de mathématiques doit être parfaitement assimilée par les étudiants de Maths Spé, s’ils souhaitent pouvoir intégrer les meilleures écoles d’ingénieurs de France. Chaque révision de cours doit se dérouler sérieusement et avec rigueur. Si certaines difficultés refont surface, il suffit de prendre le temps de bien revoir les définitions et les méthodes de cours qu’il faut connaître par cœur, vous pouvez aussi completer cela avec des cours de maths particulier. Quelques chapitres indispensables à réviser :

