Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Révision pour les écrits en MP, PC, PSI et PT
Algèbre Analyse Probabilités
Algèbre – Révision pour les écrits pour les maths spé
Plan
Les démonstrations du cours qui pourraient être demandées ainsi que les résultats classiques très proches du cours à savoir justifier.
Le temps indiqué est le temps minimum, il dépend de ce que vous avez oublié.
Selon le cas, vous trouverez la démonstration ou le lieu où trouver le résultat dans PrepApp. Elles sont en général repérées par le nouveau symbole
1. Algèbre linéaire
2. Matrices : Vandermonde et déterminants par blocs.
3. Réduction un exercice ajouté en MP/PSI
4. Préhilbertiens
5. Euclidiens un exercice
1. Exercices sur les espaces vectoriels
S1. Si ![]() et
et ![]() ,
,
![]() ssi
ssi ![]() .
.
Question 1
a) Si ![]() où
où ![]() , il existe
, il existe ![]() tel que
tel que ![]() et si
et si ![]() ,
, ![]() .
.
b) L’entier ![]() étant défini dans la question a), montrer que si
étant défini dans la question a), montrer que si ![]() ,
, ![]() .
.
Question 2
Montrer que la suite ![]() est monotone pour l’inclusion et qu’elle est stationnaire à partir du même rang
est monotone pour l’inclusion et qu’elle est stationnaire à partir du même rang ![]() .
.
Question 3
Montrer que ![]() et que la restriction de
et que la restriction de ![]() à
à ![]() est un automorphisme de
est un automorphisme de ![]()
S2. Soient ![]() un espace vectoriel de dimension
un espace vectoriel de dimension ![]() et
et ![]() tel qu’il existe
tel qu’il existe ![]() tel que
tel que ![]()
soit une base de ![]() .
.
![]() est un espace vectoriel de dimension
est un espace vectoriel de dimension ![]() et de base
et de base ![]()
S3. Soit ![]() un espace vectoriel de dimension
un espace vectoriel de dimension ![]() et
et ![]() un endomorphisme de
un endomorphisme de ![]() de rang 1.
de rang 1.
![]() .
.
S4. C’est du cours pour les MP, un exercice en PC/PSI.
Soient ![]()
![]() éléments de
éléments de ![]() , deux à deux distincts.
, deux à deux distincts.
Question 1
Pour tout ![]() de
de ![]() , il existe un unique polynôme
, il existe un unique polynôme ![]() tel que
tel que
![]() ,
, ![]() .
.
Les polynômes ![]() sont appelés polynômes d’interpolation de Lagrange sur les points
sont appelés polynômes d’interpolation de Lagrange sur les points ![]()
Question 2
Pour tout ![]() de
de ![]() ,
,
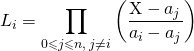 .
.
Question 3
![]() est une base de
est une base de ![]() et
et ![]() .
.
Question 4
![]() ,
, ![]() tel que
tel que ![]() ,
, ![]() , de plus
, de plus ![]() .
.
S5. Soit ![]() un espace vectoriel réel de dimension finie et
un espace vectoriel réel de dimension finie et ![]()
![]()
![]() .
.
COURS DE MATHS
Nous avons recruté pour vous les meilleurs professeurs particuliers de maths
S'EXERCER ET APPRENDRE
Avis Google France ★★★★★ 4,8 sur 5
2. Matrices
S1. Soient ![]() ,
, ![]() et
et ![]() ont même trace.
ont même trace.
Deux matrices semblables ont même trace.
S2. Soit ![]() la base canonique de
la base canonique de ![]() .
.
Question 1
Démontrer que
![]()
Question 2
Démontrer que
Si ![]() ,
,
![]()
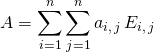 ,
,
![]()
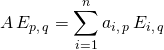
![]() et
et 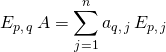 .
.
S3. Si ![]() ,
, ![]() et
et ![]() ,
, ![]() est semblable à
est semblable à

soit ![]() .
.
Ou la forme vectorielle :
Si ![]() est un endomorphisme de
est un endomorphisme de ![]() , espace vectoriel de dimension
, espace vectoriel de dimension ![]() tel que
tel que ![]() et
et ![]() , il existe une base
, il existe une base ![]() de
de ![]() dans laquelle la matrice de
dans laquelle la matrice de ![]() est la matrice
est la matrice ![]() écrite ci-dessus.
écrite ci-dessus.
S4. Soit ![]() avec
avec ![]() si
si ![]() et
et ![]() où
où ![]() .
.
Calculer ![]() pour
pour ![]() .
.
S5. Si ![]() est un
est un ![]() -espace vectoriel de dimension
-espace vectoriel de dimension ![]() et si
et si ![]() est un projecteur de
est un projecteur de ![]() ,
, ![]() .
.
S6. Déterminant de Vandermonde
Si ![]() sont des scalaires, connaitre la définition, la valeur de
sont des scalaires, connaitre la définition, la valeur de ![]() et savoir justifier le résultat.
et savoir justifier le résultat.
S7. Déterminant d’une matrice triangulaire par blocs
Soit ![]() où
où
![]() et
et ![]() .
.
Montrer que ![]() .
.
3. Réduction
S1. Comment déterminer rapidement le rang d’une matrice ![]() qui est diagonalisable ?
qui est diagonalisable ?
S2. Condition nécessaire et suffisante pour que ![]() (ou un endomorphisme en dimension finie) ayant une seule valeur propre soit diagonalisable
(ou un endomorphisme en dimension finie) ayant une seule valeur propre soit diagonalisable
S3. Si ![]() ,
, ![]() admet au moins une valeur propre
admet au moins une valeur propre
S4. Condition nécessaire et suffisante pour qu’une droite soit ![]() -stable si
-stable si ![]() est un endomorphisme de
est un endomorphisme de ![]() .
.
S5. Si ![]() et
et ![]() sont deux endomorphismes de
sont deux endomorphismes de ![]() , ev de dimension finie, qui permutent, les sous-espaces propres de
, ev de dimension finie, qui permutent, les sous-espaces propres de ![]() sont
sont ![]() -stables.
-stables.
S6. Si ![]() est un endomorphisme de l’espace vectoriel
est un endomorphisme de l’espace vectoriel ![]() de dimension finie (ou de dimension iinfinie) tel que tout vecteur non nul est vecteur propre de
de dimension finie (ou de dimension iinfinie) tel que tout vecteur non nul est vecteur propre de ![]() ,
, ![]() est une homothétie.
est une homothétie.
S7. Soient ![]() un espace vectoriel de dimension
un espace vectoriel de dimension ![]() et
et ![]() un sev de
un sev de ![]() tel que
tel que ![]() stable pour l’endomorphisme
stable pour l’endomorphisme ![]() de
de ![]() .
.
On note ![]() l’endomorphisme induit par
l’endomorphisme induit par ![]() sur
sur ![]() .
.
Question 1
Le polynôme caractéristique de ![]() divise celui de
divise celui de ![]() .
.
Question 2 (sauf PC)
Si ![]() est diagonalisable,
est diagonalisable, ![]() est diagonalisable.
est diagonalisable.
S8. ![]() est un
est un ![]() -espace vectoriel de dimension
-espace vectoriel de dimension ![]() ,
, ![]() et
et ![]() sont deux endomorphismes de
sont deux endomorphismes de ![]() qui permutent.
qui permutent.
Si ![]() admet
admet ![]() valeurs propres distinctes, toute base de vecteurs propres de
valeurs propres distinctes, toute base de vecteurs propres de ![]() est une base de vecteurs propres de
est une base de vecteurs propres de ![]() .
.
Et la version matricielle :
Si ![]() vérifient
vérifient ![]() et si
et si ![]() admet
admet ![]() valeurs propres distinctes, il existe
valeurs propres distinctes, il existe![]() et deux matrices diagonales
et deux matrices diagonales ![]() et
et ![]() telles que
telles que ![]() et
et ![]()
S9. MP et PSI seulement
![]() est un
est un ![]() -espace vectoriel de dimension
-espace vectoriel de dimension ![]() ,
, ![]() et
et ![]() sont deux endomorphismes de
sont deux endomorphismes de ![]() qui permutent.
qui permutent.
Si ![]() et
et ![]() sont diagonalisables, il existe une base de
sont diagonalisables, il existe une base de ![]() formée de vecteurs propres de
formée de vecteurs propres de ![]() et de
et de ![]() .
.
Et la version matricielle :
Si ![]() sont diagonalisables et vérifient
sont diagonalisables et vérifient ![]() , il existe
, il existe ![]() et deux matrices diagonales
et deux matrices diagonales ![]() et
et ![]() telles que
telles que ![]() et
et ![]()
S10. Soit ![]()
Question 1
![]() est de rang 1 ssi il existe
est de rang 1 ssi il existe ![]() de
de ![]() non nulles telles que
non nulles telles que ![]() .
.
Question 2
Si ![]() est de rang 1,
est de rang 1, ![]() .
.
Question 3
Si ![]() ,
, ![]() est diagonalisable ssi la trace de
est diagonalisable ssi la trace de ![]() est non nulle.
est non nulle.
S11. Matrice compagnon
Soit ![]() et
et ![]() ,
,
 ,
, 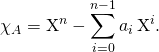
Montrer que ![]() est diagonalisable ssi le polynôme caractéristique de
est diagonalisable ssi le polynôme caractéristique de ![]() est scindé à racines simples.
est scindé à racines simples.
S12. Diagonaliser (rapidement ! ) la matrice ![]() avec
avec ![]() si
si ![]() et
et ![]() où
où ![]() .
.
En déduire le polynôme caractéristique de ![]() .
.
S13. MP/PSI
Si ![]() est un endomorphisme de matrice
est un endomorphisme de matrice ![]() dans la base
dans la base ![]() ,
, ![]() est un hyperplan
est un hyperplan ![]() -stable
-stable ![]()
![]() a pour équation dans la base
a pour équation dans la base ![]() :
: ![]() où
où ![]() est un vecteur propre de
est un vecteur propre de ![]() .
.
PC
Soit ![]() l’endomorphisme canoniquement associé à
l’endomorphisme canoniquement associé à ![]() .
.
On note ![]() le plan d’équation
le plan d’équation ![]() et
et ![]() .
.
![]() est
est ![]() -stable ssi
-stable ssi ![]() est un vecteur propre de
est un vecteur propre de ![]() .
.
S14. MP et PSI Si la matrice ![]() est diagonalisable et inversible,
est diagonalisable et inversible, ![]() est diagonalisable.
est diagonalisable.
Exercices conseillés : en MP / PSI
deuxième série d’exercices : 4 . 5. et 12
matrices stochastiques exercice 16, une approche complémentaire dans la cinquième tâche de révisions avec les probabilités.
Exercices conseillés en PC
deuxième série d’exercices : 10 . 11 . et 14
matrices stochastiques exercice 14 , une approche complémentaire dans la cinquième tâche de révisions avec les probabilités.
PROF DE MATHS PARTICULIER
Des cours de qualité et enseignants aguerris
Préparer des concours ou s'exercer
Avis Google France ★★★★★ 4,9 sur 5
4. Espaces préhilbertiens
S1. Si ![]() est un préhilbertien réel, démontrer l’inégalité de Cauchy-Schwarz :
est un préhilbertien réel, démontrer l’inégalité de Cauchy-Schwarz :![]()
Démontrer qu’il y a égalité si, et seulement si, la famille ![]() est liée.
est liée.
S2. Soit ![]() .
.
Question 1
![]()
définit un produit scalaire sur ![]() .
.
Question 2
![]() et
et ![]() sont des supplémentaires orthogonaux de
sont des supplémentaires orthogonaux de ![]() .
.
Question 3 (plus difficile et moins courante)
si ![]() .
.
S3. Sur l’espace vectoriel ![]() des fonctions continues et de carré intégrable sur l’intervalle
des fonctions continues et de carré intégrable sur l’intervalle ![]() à valeurs dans
à valeurs dans ![]() ,
, ![]()
définit un produit scalaire.
S4. Si ![]() est la projection orthogonale sur un sous-espace vectoriel
est la projection orthogonale sur un sous-espace vectoriel ![]() du préhilbertien
du préhilbertien ![]() , pour tout
, pour tout ![]() ,
, ![]() .
.
S5. Si ![]() est une base orthonormale de l’espace euclidien
est une base orthonormale de l’espace euclidien ![]() et si
et si ![]() où
où ![]() ,
, ![]()
S6. Soient ![]() un espace euclidien et
un espace euclidien et ![]() une isométrie de
une isométrie de ![]() ,
, ![]() et
et ![]() sont des supplémentaires orthogonaux.
sont des supplémentaires orthogonaux.
S7. Soit ![]() un espace euclidien de base orthonormale
un espace euclidien de base orthonormale ![]() . Soit
. Soit ![]() une base orthonormale du sous-espace vectoriel
une base orthonormale du sous-espace vectoriel ![]() .
.
Si l’on note ![]() la matrice de
la matrice de ![]() dans
dans ![]() , la matrice
, la matrice ![]() de
de ![]() dans la base
dans la base ![]() est
est 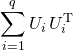 .
.
Conseil :
Les polynômes orthogonaux au programme en MP et qui peuvent faire l’objet d’un problème dans toutes les questions : méthodes paragraphes 7.1. à 7.4. attention aux racines dans l’intervalle.
(avec les polynômes de Tchebichev, vous avez sûrement un sujet de devoir dessus, ou de Hermite).
MP Seulement
Formule de Parseval
Si ![]() est une suite orthonormale totale d’éléments du préhilbertien
est une suite orthonormale totale d’éléments du préhilbertien ![]() ,
,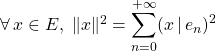 .
.
5. Euclidiens
S1. Projecteurs orthogonaux
Un projecteur ![]() est dit orthogonal lorsque
est dit orthogonal lorsque ![]() et
et ![]() sont orthogonaux.
sont orthogonaux.
Question 1
Soit ![]() un espace euclidien et
un espace euclidien et ![]() un projecteur de
un projecteur de ![]() .
. ![]() est un projecteur orthogonal si, et seulement si,
est un projecteur orthogonal si, et seulement si, ![]() est un endomorphisme symétrique.
est un endomorphisme symétrique.
Question 2
Soit ![]() un projecteur de
un projecteur de ![]() .
.
![]() est un projecteur orthogonal ssi
est un projecteur orthogonal ssi ![]()
S2. Si ![]() ,
, ![]() et
et ![]() ont même rang
ont même rang
S3. Soit ![]() un espace euclidien et
un espace euclidien et ![]() une symétrie de
une symétrie de ![]() différente de
différente de ![]() . Il y a équivalence entre :
. Il y a équivalence entre :
a) ![]() est une isométrie
est une isométrie
b) ![]() est un endomorphisme symétrique
est un endomorphisme symétrique
c) les sous espaces ![]() et
et ![]() sont des supplémentaires orthogonaux.
sont des supplémentaires orthogonaux.
On dit que ![]() est une symétrie orthogonale.
est une symétrie orthogonale.
S4. Soit ![]() euclidien de dimension
euclidien de dimension ![]() .
.
Question 1
Traduction vectorielle puis matricielle de la symétrie orthogonale ![]() par rapport à la droite
par rapport à la droite ![]() où
où ![]() .
.
Question 2
Traduction vectorielle puis matricielle de la symétrie orthogonale ![]() par rapport à l’hyperplan
par rapport à l’hyperplan ![]() où
où ![]() est un vecteur unitaire (réflexion).
est un vecteur unitaire (réflexion).
S5. Sur ![]() .
.
![]() 1. Si
1. Si ![]() est un espace euclidien et
est un espace euclidien et ![]() ,
, ![]() .
.
![]() 2. Si
2. Si ![]() ,
, ![]() .
.
![]() 3. Si
3. Si ![]() ,
, ![]() .
.
![]() 4.
4. ![]() est une partie fermée bornée (compacte en MP) de
est une partie fermée bornée (compacte en MP) de ![]() .
.
S6. Si ![]() est un endomorphisme symétrique de
est un endomorphisme symétrique de ![]() ,
, ![]() et
et ![]() sont des supplémentaires orthogonaux.
sont des supplémentaires orthogonaux.
Les sous-espaces propres de ![]() sont deux à deux orthogonaux.
sont deux à deux orthogonaux.
S7. Soient ![]() et
et ![]() deux endomorphismes symétriques de l’espace euclidien
deux endomorphismes symétriques de l’espace euclidien ![]() tels que
tels que ![]() .
.
![]() et
et ![]() sont diagonalisables dans la même base orthonormale.
sont diagonalisables dans la même base orthonormale.
S8. Soit ![]() un espace euclidien.
un espace euclidien.
Un endomorphisme ![]() symétrique de
symétrique de ![]() est dit positif si
est dit positif si ![]() ,
, ![]() .
.
Un endomorphisme ![]() symétrique de
symétrique de ![]() est dit défini positif si
est dit défini positif si
![]() ,
, ![]() .
.
Soit ![]() un endomorphisme symétrique de
un endomorphisme symétrique de ![]() . Montrer que :
. Montrer que :
![]() est positif ssi
est positif ssi ![]() ;
;
![]() est défini positif ssi
est défini positif ssi ![]() .
.
S9. Soit ![]() un endomorphisme symétrique positif. Il existe un endomorphisme symétrique
un endomorphisme symétrique positif. Il existe un endomorphisme symétrique ![]() positif tel que
positif tel que ![]() .
.
S10. Soit ![]() .
.
![]() est dite positive ssi
est dite positive ssi ![]() .
.
![]() est dite définie positive ssi
est dite définie positive ssi ![]() .
.
On note ![]() l’ensemble des matrices symétriques réelles positives et
l’ensemble des matrices symétriques réelles positives et ![]() l’ensemble des matrices symétriques réelles définies positives.
l’ensemble des matrices symétriques réelles définies positives.
Montrer que
![]()
et ![]() .
.
S11. a) Si ![]() , la matrice
, la matrice ![]() est une matrice symétrique positive.
est une matrice symétrique positive.
b) Si ![]() , la matrice
, la matrice ![]() est une matrice symétrique définie positive.
est une matrice symétrique définie positive.
S12. Si ![]() est une matrice symétrique positive, il existe
est une matrice symétrique positive, il existe ![]() symétrique positive telle que
symétrique positive telle que ![]() .
.
S13. Inégalité de Hadamard
Soit ![]() et
et ![]() .
.
On note ![]() les vecteurs colonnes de
les vecteurs colonnes de ![]() .
.
On note ![]() la norme euclidienne canonique dans
la norme euclidienne canonique dans ![]() .
.
a) Montrer que  .
.
b) Trouver une CNS pour qu’il y ait égalité
Exercices conseillés
Première série : Paragraphes 1 , 5 et 6
Deuxième série : Paragraphe 8 et 9
Troisième série : Paragraphes 5 – 6 et 8
Partie Analyse
Plan
Les démonstrations du cours qui pourraient être demandées ainsi que les résultats classiques très proches du cours à savoir justifier.
Le temps indiqué est le temps minimum, il dépend de ce que vous avez oublié.
Selon le cas, vous trouverez la démonstration ou le lieu où trouver le résultat dans PrepApp. Elles sont en général repérées par le nouveau symbole
1. Séries numériques
2. Suites et séries de fonctions
3. Séries entières
4. Intégration sur un intervalle quelconque
5. Convergence dominée et théorème d’intégration terme à terme
6. Intégrales à paramètre.
7. Espaces vectoriels normés
8. Équations différentielles
9. Fonctions de plusieurs variables
10. Familles sommables en MP.
1. Séries numériques
S1. Si ![]() est une fonction continue, décroissante et à valeurs positives ou nulles, non intégrable sur
est une fonction continue, décroissante et à valeurs positives ou nulles, non intégrable sur ![]() , trouver un équivalent de
, trouver un équivalent de 
S2. Soit ![]() une suite qui converge vers 0 et
une suite qui converge vers 0 et ![]() .
.
![]() converge
converge ![]()
![]() converge.
converge.
S3. Soit ![]() et
et ![]() un réel.
un réel.
Pour ![]() ,
, ![]() .
.
Montrer que ![]() converge.
converge.
S4. Soit ![]() .
.
![]() .
.
Montrer que ![]() converge
converge ![]()
S5. Justifier la divergence des séries de termes généraux :
![]() si
si ![]()
et ![]() si
si ![]()
S6. Un grand classique : Constante d’Euler
Convergence de la suite de terme général 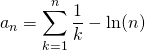 où
où ![]() .
.
Trouver un équivalent de 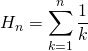
S7. Si ![]() est continue sur [0 , +
est continue sur [0 , +![]() [, décroissante et de limite nulle en
[, décroissante et de limite nulle en ![]() , la série de terme général
, la série de terme général ![]() converge.
converge.
S8. Convergence et somme de la série de terme général ![]() .
.
S9. ![]() , convergence de
, convergence de ![]() et somme.
et somme.
S10. Soit ![]() et si
et si ![]() ,
, ![]() .
.
On note  , montrer que
, montrer que ![]() .
.
S11. Soient ![]() et
et ![]() deux suites telles que :
deux suites telles que :
![]() la suite
la suite ![]() est une suite de réels décroissante, convergente de limite nulle
est une suite de réels décroissante, convergente de limite nulle
![]() la suite
la suite ![]() est une suite de complexes telle que si l’on note, pour
est une suite de complexes telle que si l’on note, pour ![]() ,
, 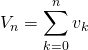 , la suite
, la suite ![]() est bornée.
est bornée.
a) On note si ![]() ,
, 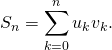
Montrer que ![]() vérifie :
vérifie :
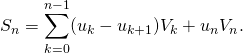
b) Montrer que ![]() converge.
converge.
S12. Révision de cours en MP et exercice en PC/PSI.
Soient ![]() et
et ![]() deux suites telles
deux suites telles ![]()
On suppose que ![]() converge.
converge.
![]() Si
Si ![]() , montrer que
, montrer que
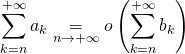 .
.
![]() Si
Si ![]() , montrer que
, montrer que
 .
.
S13. Révision de cours en MP et exercice en PC/PSI.
Soient ![]() et
et ![]() deux suites telles
deux suites telles ![]()
On suppose que ![]() diverge.
diverge.
![]() Si
Si ![]() ,
,
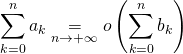 .
.
![]() Si
Si ![]() ,
,
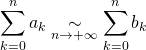 .
.
2. Suites et séries de fonctions
MP seulement
Soit ![]() une fonction continue sur
une fonction continue sur ![]() à valeurs dans
à valeurs dans ![]() telle que
telle que ![]() .
.
Alors la fonction ![]() est nulle sur
est nulle sur ![]() .
.
S1. Lorsque ![]() est continue sur
est continue sur ![]() , convergence et calcul de la somme de la série de terme général
, convergence et calcul de la somme de la série de terme général ![]() .
.
S2. Question 1 (MP/PSI)
La série de terme général ![]() converge sur
converge sur ![]() .
.
La somme ![]() tend vers
tend vers ![]() en
en ![]() .
.
Question 1 (PC)
![]() est définie sur
est définie sur ![]() par
par 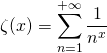 .
.
a) Montrer que la fonction ![]() admet une limite finie
admet une limite finie ![]() en
en ![]() .
.
b) Soit ![]() et
et ![]() la somme partielle et le reste d’ordre n de la série de fonctions. Déterminer
la somme partielle et le reste d’ordre n de la série de fonctions. Déterminer ![]() en démontrant que si
en démontrant que si ![]() ,
, ![]() .
.
Question 2
Soit pour ![]() ,
, ![]() .
.
![]() ne converge pas uniformément sur
ne converge pas uniformément sur ![]() .
.
En proposer deux démonstrations (une seule en PC) .
Question 3
La fonction 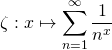 est de classe
est de classe ![]() sur
sur ![]() .
.
Question 4
Équivalent en 1 de 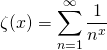 .
.
Question 5 (MP/PSI)
Soit si 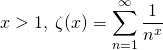 .
.
Montrer que ![]() .
.
Question 5 (PC)
En vous inspirant de la méthode utilisée dans la question 1), déterminer la limite en ![]() de
de ![]() .
.
S3. Soit si ![]() ,
, 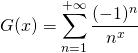 .
.
Question 1
![]() est continue sur
est continue sur ![]() .
.
Question 2.
![]() est de classe
est de classe ![]() sur
sur ![]() .
.
Question 3
Simplifier ![]() . En déduire la limite de
. En déduire la limite de ![]() en
en ![]() .
.
Exercice conseillé :
exercice 2 question 1 à 7 de la tâche exercices sur les séries de fonctions.
Ajouter la question :
La somme ![]() est intégrable sur
est intégrable sur ![]()
3. Séries entières
S1. Définition du rayon de convergence ![]() de
de ![]()
S2. Si la série de terme général ![]() vérifie les hypothèses du théorème des séries alternées et si le rayon de convergence
vérifie les hypothèses du théorème des séries alternées et si le rayon de convergence ![]() de
de ![]() est égal à 1, la somme
est égal à 1, la somme ![]() est continue sur
est continue sur ![]() .
.
S3. Ecrire ![]() comme somme d’une série entière.
comme somme d’une série entière.
On donne pour ![]()
![]() .
.
S4. Si le rayon de convergence de ![]() est égal à
est égal à ![]() , le rayon de convergence de
, le rayon de convergence de ![]() est égal à
est égal à ![]() .
.
S5. Donner le développement en série entière de ![]() , on exprimera les coefficients à l’aide de coefficients binomiaux.
, on exprimera les coefficients à l’aide de coefficients binomiaux.
S6. Montrer que la fonction ![]() est prolongeable par continuité en
est prolongeable par continuité en ![]() en une fonction de classe
en une fonction de classe ![]() sur
sur ![]() .
.
S7. Intégrale de Poisson
Question 1
Soit ![]() . Montrer que
. Montrer que ![]() est définie sur
est définie sur ![]() . La développer en série entière.
. La développer en série entière.
Montrer que le résultat obtenu est encore valable si ![]() où
où ![]() .
.
Question 2
Soit ![]() . Développer en série entière
. Développer en série entière ![]()
![]() .
.
S8. On note ![]() si
si ![]() et
et ![]() .
.
![]() est de classe
est de classe ![]() sur
sur ![]() mais n’est pas développable en série entière au voisinage de 0.
mais n’est pas développable en série entière au voisinage de 0.
Exercices conseillés :
Dans la tâche Exercices 2
I- Questions 1 à 4.
II –
III
IV –
VIII – Questions 1 et 2 au minimum.
Les cours en ligne de Maths en PC, les cours en ligne de Maths en PT, les cours en ligne de Maths en PSI et les cours en ligne de Maths en MP sont basés sur le programme de Maths Spé en vigueur. Chaque cours correspond donc aux notions de cours qui sont vues avec les professeurs en prépa.
4. Intégration sur un intervalle quelconque
Un premier savoir faire important :
Soit ![]() et
et ![]() une fonction continue et intégrable sur I à valeurs dans
une fonction continue et intégrable sur I à valeurs dans ![]() .
.
Comment justifier la dérivation de
![]() ?
?
Deuxième savoir faire important
Quelles sont les hypothèses (et éventuellement le raisonnement) qui permettent de passer de
![]()
ou de ![]()
ou de ![]()
ou de ![]()
à ![]() est nulle sur l’intervalle considéré ?
est nulle sur l’intervalle considéré ?
S1. Intégrale de Dirichlet
L’ intégrale ![]() est convergente mais non absolument convergente.
est convergente mais non absolument convergente.
S2. Intégrale de Dirichlet – autre méthode pour la convergence.
Retrouver la convergence de l’intégrale de Dirichlet en utilisant l’intégrale ![]() .
.
S3. Si l’intégrale ![]() est convergente et si
est convergente et si ![]() a une limite
a une limite ![]() en
en ![]() , cette limite est nulle.
, cette limite est nulle.
S4. Donner un exemple de fonction ![]() continue sur
continue sur ![]() telle que l’intégrale
telle que l’intégrale ![]() est convergente et sans limite en
est convergente et sans limite en ![]() , elle peut même être non bornée.
, elle peut même être non bornée.
S5. Intégrale de Bertrand : savoir choisir la bonne méthode selon le cas de l’exercice pour
![]() étudier la convergence de l’intégrale
étudier la convergence de l’intégrale ![]()
![]() étudier la convergence de l’intégrale
étudier la convergence de l’intégrale ![]()
S6. Soit ![]() . Justifier l’existence de
. Justifier l’existence de ![]() où
où ![]() et la calculer.
et la calculer.
S7. Soient ![]() et
et ![]() deux fonctions continues sur
deux fonctions continues sur ![]() et à valeurs réelles.
et à valeurs réelles.
Si les fonctions ![]() et
et ![]() sont intégrables sur
sont intégrables sur ![]() , la fonction
, la fonction ![]() est intégrable sur
est intégrable sur ![]() .
.
S8. Si ![]() , l’intégrale
, l’intégrale ![]() converge.
converge.
S9. Question 1
La fonction ![]() est définie sur
est définie sur ![]()
Question 2
![]() .
.
S10. Question 1
Soient ![]() une fonction continue sur
une fonction continue sur ![]() , dérivable en
, dérivable en ![]() et
et ![]() deux réels tels que
deux réels tels que ![]() .
.
On suppose que ![]() est intégrable sur
est intégrable sur ![]() .
.
Prouver l’existence de l’intégrale ![]() et donner sa valeur.
et donner sa valeur.
Question 2
Déterminer l’ensemble des réels ![]() tels que l’intégrale
tels que l’intégrale ![]() converge et la calculer.
converge et la calculer.
S11. Soit ![]() .
.
Question 1
Justifier l’existence de ![]() pour tout réel
pour tout réel ![]() , trouver sa limite en
, trouver sa limite en ![]() , sa dérivée, un équivalent en
, sa dérivée, un équivalent en ![]()
Question 2
Montrer que ![]() est intégrable sur
est intégrable sur ![]() et calculer son intégrale.
et calculer son intégrale.
5. Convergence dominée et intégration terme à terme
S1. Soit ![]() une fonction continue et bornée sur
une fonction continue et bornée sur ![]() .
.
Question 1
Justifier l’existence pour ![]() de
de ![]() et trouver la limite de la suite
et trouver la limite de la suite ![]() .
.
Question 2
On suppose que ![]() . Donner un équivalent de
. Donner un équivalent de ![]()
S2. Écrire ![]() comme somme d’une série. En déduire la somme de la série harmonique alternée.
comme somme d’une série. En déduire la somme de la série harmonique alternée.
S3. Montrer, en justifiant soigneusement les affirmations que si ![]() ,
, ![]() .
.
S4. Question 1
En utilisant le résultat de l’exercice précédent, donner la valeur de ![]() .
.
Rappel : si ![]() , alors
, alors ![]() .
.
Question 2
Justifier l’existence de l’intégrale de Gauss ![]() . En donner la valeur.
. En donner la valeur.
S5. Soit si ![]() .
.
Question 1
Justifier l’existence de ![]() .
.
Question 2
Déterminer ![]() dans
dans ![]() tels que
tels que 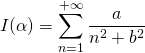 .
.
Question 3
En déduire la limite de ![]() quand
quand ![]() tend vers
tend vers ![]()
6. Intégrales à paramètre
S1. La fonction ![]() .
.
Question 1
![]() .
.
Retrouver le domaine de définition de la fonction ![]() .
.
Démontrer qu’elle est continue .
Question 2
Montrer que la fonction ![]() est de classe
est de classe ![]() sur
sur ![]() .
.
Question 3
Sens de variation de la fonction ![]() .
.
Étude aux bornes et branches infinies du graphe.
MP : Convexité de ![]() .
.
S2. Soit ![]() continue sur
continue sur ![]() et si
et si ![]()
![]() .
.
Dérivée de ![]() .
.
Vous pouvez aussi revoir dans les intégrales à paramètre :
Exercices
Les exercices 1, 2, 4 sont aussi des extraits de sujets de concours
Annales 1
Transformée de Laplace.
Annales 2
Transformée de Fourier de 1 à 7 en MP, de 1 à 6 en PC /PSI
(partie 3 moins intéressante).
Annales 3
Annales sur la fonction ![]() . parties 2 à 4.
. parties 2 à 4.
7. Espaces vectoriels normés
S1. ![]() ,
,  est une norme qui vérifie
est une norme qui vérifie ![]()
![]()
en notant ![]() lorsque
lorsque ![]() .
.
S2. Sur l’espace vectoriel ![]() des fonctions bornées sur
des fonctions bornées sur ![]() à valeurs dans
à valeurs dans ![]() : si
: si ![]() ,
, ![]() définit une norme.
définit une norme.
S3. Comparer les normes de la convergence uniforme , de la convergence en moyenne et de la convergence en moyenne quadratique sur l’espace vectoriel des fonctions continues sur ![]() à valeurs dans
à valeurs dans ![]() et démontrer qu’elles ne sont pas équivalentes.
et démontrer qu’elles ne sont pas équivalentes.
S4. Montrer que ![]() , telle que
, telle que ![]() n’a pas de limite en
n’a pas de limite en ![]() .
.
S5. Soit ![]() un espace vectoriel normé et
un espace vectoriel normé et ![]() une partie non vide de
une partie non vide de ![]() . Si
. Si ![]() , on note
, on note ![]() .
.
L’application ![]() est 1-lipschitzienne sur
est 1-lipschitzienne sur ![]() .
.
S6. Version MP Première partie
On suppose que ![]() et
et ![]() sont deux espaces vectoriels de dimension finie et
sont deux espaces vectoriels de dimension finie et ![]() ,
,
![]() les trois réels suivants sont définis et égaux :
les trois réels suivants sont définis et égaux :
![]()
![]()
![]() .
.
On l’appelle norme subordonnée de ![]() relative aux normes
relative aux normes ![]() et
et ![]() .
.
![]()
![]() .
.
![]() L’application
L’application ![]() définit une norme sur
définit une norme sur ![]() .
.
S6 Deuxième partie Version MP
Si ![]() sont des espaces vectoriels de dimensions finies, si
sont des espaces vectoriels de dimensions finies, si ![]() et
et ![]() ,
,
![]()
en notant
![]() la norme subordonnée aux normes choisies dans
la norme subordonnée aux normes choisies dans ![]() et
et ![]()
![]() la norme subordonnée aux normes choisies dans
la norme subordonnée aux normes choisies dans ![]() et
et ![]()
et ![]() la norme subordonnée aux normes choisies dans
la norme subordonnée aux normes choisies dans ![]() et
et ![]() .
.
S6. Version PC/PSI
On suppose que ![]() et
et ![]() sont des
sont des ![]() – espaces vectoriels de dimension finie. Soit
– espaces vectoriels de dimension finie. Soit ![]() .
.
On note ![]() (resp.
(resp. ![]() ) une norme sur
) une norme sur ![]() (resp.
(resp. ![]() ).
).
Question 1
Démontrer que ![]() est défini et qu’il existe
est défini et qu’il existe ![]() tel que
tel que ![]() et
et ![]() .
.
Question 2
Montrer que ![]() .
.
Question 3
On note ![]() .
.
Montrer que ![]() est une norme sur
est une norme sur ![]() .
.
S7. Soit ![]() . Soit
. Soit ![]() .
.
Si ![]() , on note
, on note![]() .
.
Montrer que ![]() existe et que
existe et que
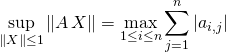 .
.
S8. MP : ![]() est un compact de
est un compact de ![]() .
.
PSI/PC : ![]() est une partie fermée bornée de
est une partie fermée bornée de ![]() .
.
En MP : espaces vectoriels normés, méthodes 2 paragraphe 10
En PC/PSI : méthodes 2 paragraphe 8
S9. MP On suppose que ![]() et
et ![]() sont des
sont des ![]() – espaces vectoriels de dimension finie. Soit
– espaces vectoriels de dimension finie. Soit ![]() .
.
On note ![]() (resp.
(resp. ![]() ) une norme sur
) une norme sur ![]() (resp.
(resp. ![]() ).
).
Démontrer que ![]() est défini et qu’il existe
est défini et qu’il existe ![]() tel que
tel que ![]() et
et ![]() .
.
S10. Si ![]() et
et ![]() ,
, ![]() et
et ![]() ont même polynôme caractéristique.
ont même polynôme caractéristique.
En MP : Espaces vectoriels normées. Méthode 2 exercice classique 1 du paragraphe 13
PC/PSI : Espaces vectoriels normés. Méthode 2 Paragraphe X.3.
S11. MP seulement
Si ![]() est un sous groupe de (
est un sous groupe de (![]() , +), il existe
, +), il existe ![]() tel que
tel que ![]() ou
ou ![]() est dense dans
est dense dans ![]() .
.
S12. ![]() C1 : si
C1 : si ![]() est une matrice diagonale,
est une matrice diagonale, ![]() ,
,
la suite ![]() converge ssi
converge ssi ![]() .
.
![]() C2 : Si
C2 : Si ![]() , la suite
, la suite ![]() converge ssi la suite
converge ssi la suite ![]() converge.
converge.
![]() C3 : Si
C3 : Si ![]() et
et ![]() et si
et si ![]() et
et ![]() ,
, ![]() .
.
![]() C4 : Toute matrice carrée
C4 : Toute matrice carrée ![]() est limite d’une suite de matrices inversibles.
est limite d’une suite de matrices inversibles.
![]() C5 : Si la suite
C5 : Si la suite ![]() converge vers
converge vers ![]() et si
et si ![]() est valeur propre de
est valeur propre de ![]() ,
, ![]() .
.
![]() C6 : Si
C6 : Si ![]() et si la suite
et si la suite ![]() converge, pour tout
converge, pour tout ![]() , la suite
, la suite ![]() converge vers
converge vers ![]() tel que
tel que ![]() (donc si
(donc si ![]() ,
, ![]() est un vecteur propre de
est un vecteur propre de ![]() associé à la valeur propre 1).
associé à la valeur propre 1).
S13. ![]() est un ouvert de
est un ouvert de ![]() .
.
S14. Soient ![]() et
et ![]() deux espaces vectoriels de dimension finie. Si
deux espaces vectoriels de dimension finie. Si ![]() (resp.
(resp. ![]() ) est un fermé de
) est un fermé de ![]() (resp
(resp ![]() ),
), ![]() est un fermé de
est un fermé de ![]() .
.
S15. Si ![]() et
et ![]() sont deux parties compactes de
sont deux parties compactes de ![]() ,
, ![]()
est une partie compacte de ![]() .
.
En PC/PSI, remplacer partie compacte par partie fermée bornée.
S16. Soit ![]() ,
, ![]() ,
, ![]() .
.
Si la suite ![]() converge vers
converge vers ![]() ,
, ![]() .
.
S17. Si ![]() est continue sur
est continue sur ![]() à valeurs dans
à valeurs dans ![]() et admet une limite
et admet une limite ![]() en
en ![]() ,
, ![]() est bornée sur
est bornée sur ![]()
S18. L’ensemble des matrices carrées d’ordre ![]() symétriques et à valeurs propres positives ou nulles et une partie fermée de
symétriques et à valeurs propres positives ou nulles et une partie fermée de ![]() .
.
S19. L’ensemble des projecteurs orthogonaux de l’espace euclidien ![]() est une partie fermée bornée de
est une partie fermée bornée de ![]() .
.
S20. Soit ![]() un
un ![]() – espace vectoriel de dimension finie et
– espace vectoriel de dimension finie et ![]() une norme sur
une norme sur ![]() . Il existe un réel
. Il existe un réel ![]() tel que
tel que ![]() ,
, ![]() .
.
S21. Soit ![]() un
un ![]() – espace vectoriel de dimension finie et
– espace vectoriel de dimension finie et ![]() une norme sur
une norme sur ![]() et
et ![]() une norme sur
une norme sur ![]()
Il existe un réel ![]() tel que
tel que ![]() ,
, ![]() .
.
S22. Soit ![]() un espace vectoriel euclidien et
un espace vectoriel euclidien et ![]() un endomorphisme symétrique.
un endomorphisme symétrique.
On définit ![]() et
et ![]() .
.
Question 1
Montrer que ![]() admet un maximum sur
admet un maximum sur ![]() atteint en
atteint en ![]() .
.
Question 2.
On introduit ![]() unitaire et orthogonal à
unitaire et orthogonal à ![]() Soit si
Soit si ![]() ,
, ![]() et
et ![]() .
.
a) Montrer que ![]()
b) En déduire que ![]() .
.
Question 3
Montrer que ![]() est un vecteur propre de
est un vecteur propre de ![]() .
.
8. Equations différentielles
S1. Exprimer la solution générale de ![]()
où ![]() et
et ![]() sont des fonctions continues sur un intervalle
sont des fonctions continues sur un intervalle ![]() à valeurs dans
à valeurs dans ![]() à l’aide d’intégrales
à l’aide d’intégrales
S2. Transformer l’équation différentielle linéaire d’ordre ![]() :
: 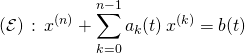 en une équation vectorielle d’ordre 1.
en une équation vectorielle d’ordre 1.
Savoir le faire sans hésiter dans le cas particulier ![]() .
.
Dans la suite (questions S3 à S5) , ![]() ,
, ![]() sont des fonctions continues sur l’intervalle
sont des fonctions continues sur l’intervalle ![]() à valeurs dans
à valeurs dans ![]() et
et ![]() :
: ![]() .
.
S3. Si ![]() et si
et si ![]() est solution de
est solution de ![]() et vérifie
et vérifie ![]() , alors
, alors ![]() .
.
S4. ![]() , justifier :
, justifier :
![]() il existe un unique couple
il existe un unique couple ![]() de solutions de
de solutions de ![]() vérifiant
vérifiant
![]()
![]() .
.
![]()
![]() est une base de
est une base de ![]() .
.
S5. Si ![]() et
et ![]() sont solutions de
sont solutions de ![]() , la fonction
, la fonction ![]() définie, pour tout
définie, pour tout ![]() , par
, par ![]() est solution d’une équation linéaire du premier ordre à donner
est solution d’une équation linéaire du premier ordre à donner
S6. Equations d’Euler
![]() où
où ![]() .
.
Retrouver l’équation différentielle en utilisant le changement de variable ![]() .
.
S7. Retrouver l’équation différentielle obtenue par la méthode de Lagrange
On suppose que l’on doit résoudre ![]() quand
quand
a) les fonctions ![]() et
et ![]() sont continues sur l’intervalle
sont continues sur l’intervalle ![]() et
et ![]() ne s’annule pas sur l’intervalle
ne s’annule pas sur l’intervalle ![]() .
.
b) on connaît une solution particulière ![]() de
de ![]() ne s’annulant pas sur
ne s’annulant pas sur ![]() .
.
S8. On suppose que l’on connaît deux solutions ![]() et
et ![]() formant une base de l’espace vectoriel des solutions de
formant une base de l’espace vectoriel des solutions de ![]()
La méthode de variation des constantes consiste à trouver deux fonctions ![]() et
et ![]() de classe
de classe ![]() sur
sur ![]() telles que
telles que ![]() soit solution de
soit solution de
![]()
avec la condition ![]() .
.
Retrouver le système à résoudre
S9. Soit ![]() .
.
Résoudre l’équation ![]() où la fonction
où la fonction ![]() est continue sur l’intervalle
est continue sur l’intervalle ![]() en utilisant la méthode de variation des constantes.
en utilisant la méthode de variation des constantes.
S10. Soient ![]() et
et ![]() deux fonctions continues sur
deux fonctions continues sur ![]() et
et ![]() -périodiques où
-périodiques où ![]() .
.
On note ![]() :
: ![]() .
.
Une solution ![]() de
de ![]() est
est ![]() -périodique ssi
-périodique ssi ![]() et
et ![]() .
.
UN PROF DE MATHS POUR EXCELLER
La pratique et la compréhension
clés de la réussite
Cours de maths en ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
9. Fonctions de plusieurs variables
En MP : travailler les méthodes (la recherche d’extremum local sur un ouvert est plutôt un exercice d’oral, par contre ce n’est pas le cas pour la recherche d’extremum global sur un compact).
Il est important de savoir passer en polaire, calculer les dérivées partielles par rapport à ![]() et
et ![]() en fonction de celles par rapport à
en fonction de celles par rapport à ![]() et
et ![]() et vice-versa.
et vice-versa.
N’oubliez pas : vous devez savoir écrire une équation
![]() de la tangente en un point régulier
de la tangente en un point régulier ![]() à la courbe définie par
à la courbe définie par ![]() .
.
![]() du plan tangent en un point régulier
du plan tangent en un point régulier ![]() de la surface d’équation cartésienne
de la surface d’équation cartésienne ![]() .
.
Les exercices à revoir
Première série : tout le paragraphe 1 ; question 1 du paragraphe 2, les paragraphes 3 et 4
Deuxième série : l’exercice 3
Troisième série : les exercices 1 et 3.
En PC/PSI : travailler les méthodes (la recherche d’extremum local sur un ouvert est plutôt un exercice d’oral, par contre ce n’est pas le cas pour la recherche d’extremum global sur un compact).
Il est important de savoir passer en polaire, calculer les dérivées partielles par rapport à ![]() et
et ![]() en fonction de celles par rapport à
en fonction de celles par rapport à ![]() et
et ![]() et vice-versa.
et vice-versa.
N’oubliez pas : vous devez savoir écrire une équation
![]() de la tangente en un point régulier
de la tangente en un point régulier ![]() à la courbe définie par
à la courbe définie par ![]() .
.
![]() du plan tangent en un point régulier
du plan tangent en un point régulier ![]() de la surface d’équation cartésienne
de la surface d’équation cartésienne ![]() .
.
Les exercices à revoir
Première série : exercices 1 et 2 du paragraphe 1 ; question 1 du paragraphe 2, les paragraphes 3 et 4
Deuxième série : l’exercice 3
Troisième série : les exercices 1 et 3.
Il y a aussi des problèmes un peu « sadiques » (pour le candidat et pour le correcteur) qui demandent de calculer ![]() et
et ![]() en fonction des dérivées partielles de
en fonction des dérivées partielles de ![]() lorsque
lorsque ![]() .
.
10. Familles sommables en MP
S1. Soit une famille dénombrable ![]() de réels positifs ou nuls.
de réels positifs ou nuls.
On considère une suite ![]() de parties finies de
de parties finies de ![]() telle que si
telle que si ![]() ,
, ![]() et
et 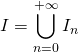 .
.
La famille ![]() est une famille sommable ssi la suite
est une famille sommable ssi la suite ![]() où
où ![]() est convergente.
est convergente.
Dans ce cas, 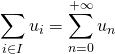 .
.
S2. Soit ![]() et
et ![]() si
si ![]() .
.
Ensemble des réels ![]() tels que la famille double
tels que la famille double ![]() soit sommable. Valeur de la somme.
soit sommable. Valeur de la somme.
S3. La série de terme de terme général ![]() si
si ![]() est convergente et calcul de la somme.
est convergente et calcul de la somme.
S4. a) Si ![]() converge absolument,
converge absolument, 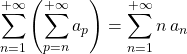 .
.
b) Si ![]() est une variable aléatoire à valeurs dans
est une variable aléatoire à valeurs dans ![]() admettant une espérance,
admettant une espérance, 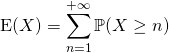 .
.
Exercices conseillés
Exercice 3
Exercices 6 et 7 plus difficiles
Probabilités
Plan
Les démonstrations du cours qui pourraient être demandées ainsi que les résultats classiques très proches du cours à savoir justifier.
Le temps indiqué est le temps minimum (en PC/PSI) , il dépend de ce que vous avez oublié.
1. Les matrices stochastiques (concerne les espaces vectoriels normés, la diagonalisation et les probabilités). Vous pourrez aussi voir le paragraphe 7 dans le chapitre Réduction deuxième série d’exercices
2. Des problèmes d’interversion de signes ![]() .
.
3. Dénombrements
4. Probabilités
5. Variables aléatoires.
1. Les matrices stochastiques
Soit ![]() .
.
On note ![]() l’ensemble des matrices stochastiques d’ordre
l’ensemble des matrices stochastiques d’ordre ![]() c’est-à-dire l’ensemble des matrices
c’est-à-dire l’ensemble des matrices ![]() à coefficients positifs ou nuls tels que
à coefficients positifs ou nuls tels que ![Rendered by QuickLaTeX.com \quad \quad \forall \, i \in [\![1 , \, n]\!], \displaystyle \sum _{j = 1} ^n a_{i ,j} = 1](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-d233d08c2846db8bd4e6f7e514267db5_l3.png) .
.
On munit ![]() de la norme définie lorsque
de la norme définie lorsque ![]() par
par ![]() .
.
Question 1
On note ![]() dont tous les éléments sont égaux à 1.
dont tous les éléments sont égaux à 1.
Montrer que ![]() à coefficients positifs ou nuls est stochastique ssi
à coefficients positifs ou nuls est stochastique ssi ![]() .
.
Question 2
Montrer que ![]() est une partie stable pour la multiplication et fermée dans
est une partie stable pour la multiplication et fermée dans ![]() .
.
Question 3
Soit ![]() .
.
a) Montrer que 1 est valeur propre de ![]() .
.
b) Montrer que pour tout ![]()
![]() .
.
c) En déduire que toute valeur propre de ![]() est de module inférieur ou égal à 1.
est de module inférieur ou égal à 1.
Question 4.
On suppose que ![]() .
.
a) Soit ![]() tel que
tel que ![]() .
.
Montrer que ![]() .
.
b) En déduire que ![]()
Question 5
Soit ![]() .
.
On note si ![]() ,
,  .
.
On note ![]() la matrice de la projection de
la matrice de la projection de ![]() sur
sur ![]() parallèlement à
parallèlement à ![]()
a) Soit ![]() , on écrit
, on écrit ![]() avec
avec ![]() et
et ![]() .
.
Montrer que ![]() .
.
b) Montrer que ![]() puis
puis ![]() .
.
Il y a bien d’autres résultats ….
Les résultats ci-dessus sont inspirés d’un sujet Mines Ponts PC/PSi 2017 et d’un sujet Epita 2015.
Vous pouvez aussi retrouver d’autres résultats sur les matrices stochastiques dans le dernier paragraphe de la deuxième série d’exercices dans le chapitre Réduction.
Revoir le paragraphe des méthodes Probabilités sur les chaînes de Markov pour leur utilisation en Probabilités.
2. Sur les interversions de signes 
S1. Intervertir les signes ![]() dans :
dans :
a) 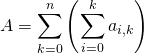
b) 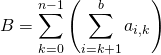 .
.
S2. Soit ![]() une variable aléatoire sur
une variable aléatoire sur ![]() telle que
telle que ![]() où
où ![]() .
.
On suppose que ![]() est une variable aléatoire telle que si
est une variable aléatoire telle que si ![]() ,
, ![]() suit une loi uniforme sur
suit une loi uniforme sur ![]() .
.
Calculer l’espérance de ![]() .
.
S3. Soit ![]()
Soit ![]() une famille de réels.
une famille de réels.
Donner une condition suffisante permettant d’écrire :
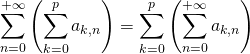 .
.
S4. Pour PC et PSI
Sommes doubles de réels positifs ou nuls.
Soit ![]() .
.
On suppose que ![]() , la série
, la série ![]() converge et a pour somme
converge et a pour somme ![]() et que
et que ![]() converge et a pour somme
converge et a pour somme ![]() .
.
a) Montrer que ![]() ,
, ![]() converge. On note
converge. On note ![]() sa somme.
sa somme.
b) Montrer que ![]() converge. On note
converge. On note ![]() sa somme. Montrer que
sa somme. Montrer que ![]() .
.
c) Montrer que ![]() .
.
On dit que la série double de réels positifs ![]() converge, dans ce cas on peut écrire :
converge, dans ce cas on peut écrire :
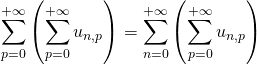 .
.
Il existe un résultat de même type avec des séries absolument convergentes qui est alors donné par l’énoncé.
S5. Soit ![]() une famille de réels positifs ou nuls.
une famille de réels positifs ou nuls.
Donner une condition suffisante permettant d’assurer l’existence de :
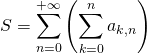 et donner une autre expression de
et donner une autre expression de ![]() .
.
S6. Soit ![]() une variable aléatoire sur
une variable aléatoire sur ![]() telle que
telle que ![]() .
.
On suppose que ![]() est une variable aléatoire telle que si
est une variable aléatoire telle que si ![]() , la variable
, la variable ![]() suit une loi uniforme sur
suit une loi uniforme sur ![]() .
.
Montrer que ![]() admet une espérance et la calculer.
admet une espérance et la calculer.
3. Dénombrements
S1. L’ application ![]() définit une bijection qui permet de démontrer que
définit une bijection qui permet de démontrer que ![]() est dénombrable.
est dénombrable.
S2. L’application : ![]()
![]() est une bijection.
est une bijection.
S3. Nombre de listes strictement croissantes de ![]() éléments de
éléments de ![]() .
.
S4. Nombre de solutions entières de l’équation ![]() .
.
S5. Application de la formule du triangle de Pascal pour calculer 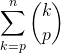 lorsque
lorsque ![]()
S6. Par application de la formule du binôme, calculer si ![]() ,
, 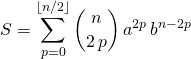 .
.
S7. Soient ![]() et
et ![]() trois entiers naturels non nuls avec
trois entiers naturels non nuls avec ![]() .
.
En utilisant un raisonnement de dénombrement, démontrer la formule de Vandermonde :
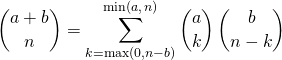 .
.
4. Probabilités
S1. Si pour tout entier ![]() ,
, ![]() est un événement négligeable (de probabilité nulle), démontrer que leur réunion est négligeable.
est un événement négligeable (de probabilité nulle), démontrer que leur réunion est négligeable.
S2. Soit ![]() une suite d’événements mutuellement indépendants et
une suite d’événements mutuellement indépendants et 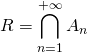 .
.
Montrer que 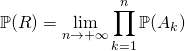 .
.
S3. On a deux urnes contenant respectivement une proposition ![]() et
et ![]() de boules blanches. Le premier tirage a lieu dans la première urne.
de boules blanches. Le premier tirage a lieu dans la première urne.
Puis si l’on obtient une boule blanche, le tirage suivant se fait dans l’urne 1 sinon il se fait dans l’urne 2.
Si ![]() est la probabilité d’obtenir une boule blanche au
est la probabilité d’obtenir une boule blanche au ![]() -ème tirage, trouver une relation de récurrence liant
-ème tirage, trouver une relation de récurrence liant ![]() et
et ![]() .
.
S4. Dans une suite d’épreuves indépendantes de pile (probabilité ![]() ) et face (probabilité
) et face (probabilité ![]() ), on gagne en obtenant la suite
), on gagne en obtenant la suite ![]() . Quelle est la probabilité de gagner ?
. Quelle est la probabilité de gagner ?
S5. On lance une pièce donnant pile avec la probabilité ![]() jusqu’à obtenir le troisième pile.
jusqu’à obtenir le troisième pile.
Quelle est la probabilité de lancer la pièce ![]() fois (avec
fois (avec ![]() ) ?
) ?
S6. Soit ![]() une suite d’événements de l’espace probabilisé
une suite d’événements de l’espace probabilisé ![]() .
.
a) L’ensemble ![]() des
des ![]() appartenant à une infinité d’éléments de la suite
appartenant à une infinité d’éléments de la suite ![]() est un événement.
est un événement.
b) L’ensemble ![]() des
des ![]() appartenant à tous les
appartenant à tous les ![]() à partir d’un certain rang est un événement.
à partir d’un certain rang est un événement.
S7. Quelques modélisations :
tout le paragraphe 2 du QCM.
S8. Soit ![]() un espace probabilisé.
un espace probabilisé.
Si ![]() et
et ![]() sont des événements indépendants,
sont des événements indépendants,
![]() lorsque
lorsque ![]() est négligeable,
est négligeable, ![]() et
et ![]() sont indépendants.
sont indépendants.
![]() lorsque
lorsque ![]() est presque sûr,
est presque sûr, ![]() et
et ![]() sont indépendants.
sont indépendants.
Exercices conseillés dans Exercices
Paragraphes 2, 3 , 7 et 8.
5. Variables aléatoires
S1. Soit ![]() . On place au hasard
. On place au hasard ![]() boules distinctes dans
boules distinctes dans ![]() tiroirs numérotés de 1 à
tiroirs numérotés de 1 à ![]() .
.
On note ![]() le nombre de tiroirs vides.
le nombre de tiroirs vides.
1. Calculer l’espérance et la variance de ![]() .
.
2. En trouver un équivalent si ![]()
S2. a) Fonction génératrice de ![]() si
si ![]() et
et ![]() sont indépendantes à valeurs dans
sont indépendantes à valeurs dans ![]() .
.
b) Lorsque ![]() sont indépendantes et à valeurs dans
sont indépendantes et à valeurs dans ![]() , fonction génératrice de
, fonction génératrice de 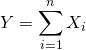 .
.
S3. Un exercice classique paragraphe VIII dans les Méthodes.
S4. Si ![]() est une variable aléatoire réelle discrète ayant un moment d’ordre 2,
est une variable aléatoire réelle discrète ayant un moment d’ordre 2, ![]() admet une espérance mathématique.
admet une espérance mathématique.
S5. Si ![]() est une variable aléatoire discrète et si
est une variable aléatoire discrète et si ![]() est bornée,
est bornée, ![]() admet une espérance mathématique.
admet une espérance mathématique.
S6. Si ![]() est une variable aléatoire réelle discrète presque sûrement constante égale à
est une variable aléatoire réelle discrète presque sûrement constante égale à ![]() ,
, ![]() admet une espérance mathématique égale à
admet une espérance mathématique égale à ![]() .
.
S7. Soit ![]() une variable aléatoire à valeurs dans
une variable aléatoire à valeurs dans ![]() .
.
a) ![]() admet une espérance mathématique ssi
admet une espérance mathématique ssi ![]() converge
converge
b) Dans ce cas : 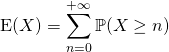 .
.
S8. Soient ![]() et
et ![]() des variables aléatoires indépendantes de loi géométrique de paramètres
des variables aléatoires indépendantes de loi géométrique de paramètres ![]() et
et ![]() .
.
La variable ![]() suit une loi géométrique de paramètre
suit une loi géométrique de paramètre ![]()
S9. Soit ![]() une variable aléatoire discrète admettant une variance nulle, en utilisant l’inégalité de Bienaymé-Tchebichev, montrer que
une variable aléatoire discrète admettant une variance nulle, en utilisant l’inégalité de Bienaymé-Tchebichev, montrer que ![]() .
.
S10. Si ![]() et
et ![]() sont deux variables aléatoires indépendantes de lois
sont deux variables aléatoires indépendantes de lois ![]() et
et ![]() , loi de
, loi de ![]()
S11. Si ![]() suit une loi de Poisson de paramètre
suit une loi de Poisson de paramètre![]() et si les variables sont indépendantes, loi de la somme.
et si les variables sont indépendantes, loi de la somme.
S12. On suppose que ![]() sont indépendantes et de loi géométrique de paramètre
sont indépendantes et de loi géométrique de paramètre ![]() . On note
. On note  .
.
Déterminer la loi de ![]() .
.
Les autres démonstrations à savoir faire, (allez dans votre cours)
Inégalité de Markov.
Inégalité de Bienaymé-Tchebichev
Loi faible des grands nombres.
CNS pour qu’une variable ait une variance nulle. ou par la question 23 du QCM
Exercices conseillés
Première série : Paragraphe 7
Deuxième série : Paragraphes 2, 4 et 7
Troisième série : Paragraphes 8 , 10 en MP, 11 et 13
COURS DE MATHS A DOMICILE
Les meilleurs profs de maths pour
réussir sa scolarité
En ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
Annales de mathématiques en maths spé
Toutes les annales pour les étudiants en Maths Spé, en PC, MP, PSI, et PT peuvent être consultées dans la rubrique Annales Maths Spé.
Pour réussir les épreuves écrites de mathématiques du concours Centrale Supélec, de l’X et l’ENS, de Mines Ponts ou encore de Mines Télécom absolument tous les chapitres de maths doivent être parfaitement assimilés et ne présenter aucune difficulté. Quelques chapitres de maths classiques à réviser seul/e ou avec un prof particulier de maths :

