Cours en ligne Maths en Maths Spé

Chapitres Maths en MP, PSI, PC, TSI, PT

Cours en ligne Maths en Maths Spé

Chapitres Maths en MP, PSI, PC, TSI, PT

Cours et méthodes sur les équivalents en Maths Spé

Name: Groupe Réussite: Cours particuliers, stages intensifs de révision
Brand: Groupe Réussite
SKU: Cours Particuliers
Rating: 4.8 (1000 reviews)

Résumé de cours Exercices et corrigés

Ce résumé de cours et de méthodes sur les équivalents en maths spé reprend les résultats déjà vus en maths sup et liste tout ce qu’il faut savoir pour les concours sur ce chapitre. Pour travailler de manière plus précise sur les équivalents et sur les autres chapitres, contactez un des professeurs Groupe Réussite pour des cours à domicile en maths.

1. Équivalents usuels et classiques en prépa Maths spé

Équivalents en 0 :

$\ast$ $\displaystyle \sin x \underset{x\rightarrow 0}{ \sim} x$

$\ast$ $\displaystyle 1-\cos x \underset{x\rightarrow 0}{ \sim} \frac{x^2}{2}$

$\ast$ $\displaystyle\tan x \underset{x\rightarrow 0}{ \sim} x$

$\ast$ $\displaystyle \ln(1+x) \underset{x\rightarrow 0}{ \sim} x$

$\ast$ $\displaystyle\textrm e^x-1 \underset{x\rightarrow 0}{ \sim} x$

$\ast$ $\displaystyle(1+x)^\alpha-1 \underset{x\rightarrow 0}{ \sim} \alpha x$

$\ast$ $\displaystyle\textrm{Arcsin } x \underset{x\rightarrow 0}{ \sim} x$

$\ast$ $\displaystyle \textrm{Arctan } x \underset{x\rightarrow 0}{ \sim} x$

$\ast$ $\displaystyle \textrm {sh}(x ) \underset{x\rightarrow 0}{ \sim} x$

$\ast$ $\displaystyle\textrm {ch}(x) -1 \underset{x\rightarrow 0}{ \sim} \frac{x^2}{2}$

$\ast$ $\displaystyle\textrm {th} (x) \underset{x\rightarrow 0}{ \sim} x$

Tous ces équivalents peuvent être retrouvés par exemple en prenant le premier terme non nul du développement limité de la fonction considérée en 0. Ces équivalents vous serviront dans le chapitre séries entières en prépa.

Équivalents classiques en 1 à connaitre

$\ast$ $\displaystyle\ln x \underset{x\rightarrow 1}{ \sim} x-1$

$\ast$ $\displaystyle\textrm{Arccos }(x) \underset{x\rightarrow 1^-}{ \sim} \sqrt{1-x^2}$

Equivalents en $\pm \infty$

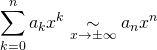$\ast$ $\displaystyle \sum_{k=0}^{n}a_k x^k \underset{x\rightarrow \pm \infty}{ \sim} a_n x^n$ si $a_n\neq 0$

$\ast$ $\displaystyle \textrm{ch } x \underset{x\rightarrow +\infty}{ \sim} \dfrac{e^x}{2}$

$\ast$ $\displaystyle \textrm{sh }x \underset{x\rightarrow +\infty}{ \sim} \dfrac{e^x}{2}$ .

PROF DE MATHS PARTICULIER

Des cours de qualité et enseignants aguerris

Préparer des concours ou s'exercer

Avis Google France ★★★★★ 4,9 sur 5

2. Opérations autorisées sur les équivalents en MP, MPI, PC, PSI, PT

Produit d’équivalents :

$f(x)\underset{x\rightarrow a}{ \sim} g(x)$ et $h(x)\underset{x\rightarrow a}{ \sim} k(x)$

$\Rightarrow$ $f(x)\,h(x)\underset{x\rightarrow a}{ \sim} g(x)\,k(x)$

Quotient d’équivalents :

$f(x)\underset{x\rightarrow a}{ \sim} g(x)$ et

$h(x)\underset{x\rightarrow a}{ \sim} k(x)$ et $h(x)\,k(x)\neq0$ $\Rightarrow$ $\displaystyle\frac{f(x)}{h(x)}\underset{x\rightarrow a}{ \sim} \frac{g(x)}{k(x)}$

Passage à la valeur absolue :

$f(x)\underset{x\rightarrow a}{ \sim} g(x)$ $\Rightarrow$ $|f(x)|\underset{x\rightarrow a}{ \sim} |g(x)|$

Puissance :

$f(x)\underset{x\rightarrow a}{ \sim} g(x)$ $\Rightarrow$ $(f(x)) ^\alpha\underset{x\rightarrow a}{ \sim} (g(x))^\alpha$

(en imposant si $\alpha\notin \mathds{Z},$ $f$ et $g$ à valeurs strictement positives).

3. Opérations interdites sur les équivalents

Une vérification qui peut aider à corriger des fautes : si la fonction ou la suite n’est pas nulle, on ne peut pas trouver un équivalent égal à 0.

Addition :

$\textrm e^{-x}-1\underset{x\rightarrow 0}{ \sim}-x$ ,

$x\underset{x\rightarrow 0}{ \sim}x$ et $\displaystyle \textrm e^{-x}-1+x\underset{x\rightarrow 0}{ \sim}\frac{x^2}{2}$ et n’est pas équivalent à 0.

Différence :

$1\underset{x\rightarrow 0}{ \sim} \, 1$ , $\cos(x) \underset{x\rightarrow 0}{ \sim} 1$ et $\displaystyle 1-\cos x\underset{x\rightarrow 0}{ \sim}\frac{x^2}{2}$ et n’est pas équivalent à 0.

Passage au logarithme pour des fonctions admettant 1 pour limite :

$u\underset{x\rightarrow a}{ \sim}v$ et $\displaystyle\lim_a v=1$ n’implique pas que $\ln \;u\underset{x\rightarrow a}{ \sim}\ln \;v$ .

Exemple :

$1+x\underset{x\rightarrow 0}{ \sim}1+x^2$ et $\ln(1+x)\underset{x\rightarrow 0}{ \sim}x$ alors que

$\ln(1+x^2)\underset{x\rightarrow 0}{ \sim}x^2$ donc $\ln(1+x)$ et $\ln(1+x^2)$ ne sont pas équivalents en 0.

Passage à l’exponentielle :

$u\underset{x\rightarrow a}{ \sim}v$ et $\displaystyle\lim_a v=\pm \infty$ n’implique pas que $\textrm e^u\underset{x\rightarrow a}{ \sim}\textrm e^v$ .

Exemple :

$u(x) = x + 1$ est équivalent à $v(x) = x$ en $+\infty$ mais $e^u$ n’est pas équivalent à $\textrm e^v,$ car le quotient $\textrm e^1$ ne tend pas vers 1.

Passage à la puissance :

$\ast$ $u\underset{x\rightarrow a}{ \sim}v$ n’implique pas $w^u\underset{x\rightarrow a}{ \sim}w^v$ et n’implique pas que $u^w\underset{x\rightarrow a}{ \sim}v^w$ lorsque $w$ n’est pas une constante.

$\ast$ De même, $u_n\underset{x\rightarrow +\infty}{ \sim}v_n$ n’implique pas $u_n^n\underset{x\rightarrow +\infty}{ \sim}v_n^n$

Exemple 1 :

$\ast$ $u(x) = x + 1$ est équivalent à $v(x) = x$ en $+\infty$ , mais $x^{x+1}$ n’est pas équivalent à $x^{x}$ car le quotient $x$ tend vers $+\infty$ .

$\ast$ De même $(x + 1)^x$ n’est pas équivalent à $x^x$ en $+\infty$ car le quotient $\displaystyle \left(1 + \frac{1}{x}\right)^x$ tend vers e en $+\infty$ .

Exemple 2 :

soit $\displaystyle u_n = 1 + \frac{1}{n}$ et $v_n = 1$ , $u_n\underset{x\rightarrow +\infty}{ \sim}v_n$ ,

$\displaystyle\lim_{n\rightarrow+\infty}u_n^n=\textrm e^1>0$ et $v_n^n=1$ ,

$u_n^n$ et $v_n^n$ ne sont pas équivalents.

N’hésitez pas à consulter tous les autres cours en ligne de Maths en MP, mais aussi les cours en ligne de Maths en PC, les cours en ligne de Maths en PSI ou encore les cours en ligne de Maths en PT pour améliorer vos résultats avant les concours.

4 – Des méthodes pour obtenir des équivalents usuels

$\bullet$ M1. Utilisation de la limite :

Si $f$ admet une limite finie non nulle $\lambda$ en $a$ , $f(x) \underset{x\rightarrow a}{ \sim}\lambda$ .

$\bullet$ M2. Utilisation de la dérivée :

Si $f$ est dérivable en $a$ et si $f '(a)$ est non nul, $f(x)-f(a) \underset{x\rightarrow a}{ \sim}f'(a)(x-a)$ .

Exemple : $\displaystyle\textrm{Arctan} (x)-\frac{\pi}{4}\underset{x\rightarrow 1}{ \sim}\frac{x-1}{2}$

$\bullet$ M3. Si $f$ et $g$ sont des fonctions à valeurs dans $\left.\right]0 , + \infty\left[\right.$ , de limite nulle en $a$ vérifiant $f(x) \underset{x\rightarrow a}{ \sim} g(x)$ , pour démontrer que $\ln(f(x)) \underset{x\rightarrow a}{ \sim} \ln(g(x))$ ,

on écrit $f(x) = g(x) (1 + \varepsilon(x))$ avec $\displaystyle\lim_{x\rightarrow a}\varepsilon(x)=0$ .

Les fonctions utilisées étant à valeurs strictement positives, on peut écrire

$\ln(f(x)) = \ln(g(x)) + \ln(1 + \varepsilon(x)).$

Comme $\displaystyle\lim_{x\rightarrow a}\ln(g(x))=-\infty$ , au voisinage de $a$ , $\ln(g(x)) \neq 0$ donc

$\ln(f(x))=\ln(g(x))\displaystyle\left(1+\frac{\ln(1+\varepsilon(x))}{\ln(g(x))} \right)$ avec

$\displaystyle\lim_{x\rightarrow a}\frac{\ln(1+\varepsilon(x))}{\ln(g(x))}=0$ donc $\ln(f(x))\underset{x\rightarrow a}{ \sim} \ln(g(x)).$

Exemple : $\ln(\sin (x))\underset{x\rightarrow 0}{ \sim}\ln (x)$

PROF DE MATHS PARTICULIER

Des cours de qualité et enseignants aguerris

Préparer des concours ou s'exercer

Avis Google France ★★★★★ 4,9 sur 5

$\bullet$ M4. Si $f$ et $g$ sont des fonctions à valeurs dans $\left.\right]0 , + \infty\left[\right.$ , de limite égale à

$+\infty$ en $a$ vérifiant $f(x) \underset{x\rightarrow a}{ \sim} g(x)$ , pour démontrer que: $\ln(f(x)) \underset{x\rightarrow a}{ \sim} \ln(g(x))$ ,

on écrit $f(x) = g(x) (1 + \varepsilon(x))$ avec $\displaystyle\lim_{x\rightarrow a}\varepsilon(x)=0.$

Les fonctions utilisées étant à valeurs strictement positives, on peut écrire $\ln(f(x)) = \ln(g(x)) + \ln(1 + \varepsilon(x)).$

Comme $\displaystyle\lim_{x\rightarrow a}\ln(g(x))=+\infty$ , au voisinage de $a$ , $\ln(g(x)) \neq 0$ donc

$\ln(f(x))=\ln(g(x))\displaystyle\left(1+\frac{\ln(1+\varepsilon(x))}{\ln(g(x))} \right)$ avec

$\displaystyle\lim_{x\rightarrow a}\frac{\ln(1+\varepsilon(x))}{\ln(g(x))}=0$ donc $\quad\quad \ln(f(x))\underset{x\rightarrow a}{ \sim} \ln(g(x))$ .

Exemple : $\ln(1+x)\underset{x\rightarrow +\infty}{ \sim}\ln (x)$

$\bullet$ M5. Par utilisation de la propriété $f = g + h$ et $h\underset{a} { = } o(g)$ , alors $f \underset {a}\sim g$ .

conséquence :

Si $f = g + h$ où $\displaystyle\lim_a g=+\infty$ et $\displaystyle\lim_a h=\lambda\in \mathds{R}$ , $f\underset{a}{ \sim}g$ , par utilisation de la propriété précédente car $h = o(g).$

Exemple :

$\ln(x)+\textrm{Arctan } x\underset{x\rightarrow +\infty}{ \sim}\ln(x)$

$\bullet$ M6. Cas d’une somme de fonctions, lorsque l’une au moins tend vers $\infty$ .

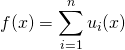Si $f(x)=\displaystyle\sum_{i=1}^{n}u_i(x)$ , l’une au moins des fonctions tendant vers $\infty$ , on met en facteur la fonction qui tend le plus vite vers l’infini.

Exemple : équivalent en $+\infty$ de

$u(x)=x^2+x^{\frac{3}{2}}\displaystyle\sin\left(\frac{1}{x}\right)+x\ln (x);$

$\bullet$ M7. Cas d’une somme de fonctions, chacune des fonctions admettant 0 pour limite.

Si 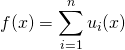$f(x)=\displaystyle\sum_{i=1}^{n}u_i(x)$ , et si pour tout $i$ , la fonction $u_i$ admet 0 pour limite en $a$ , on met en facteur la fonction qui tend le moins vite vers 0.

Exemple : trouver un équivalent en $0^+$ , de $u(x)=x+x^2\ln(x)+x\ln^2x$

Tous les chapitres au programme de Maths en Maths Spé sont également disponibles en cours en ligne, vous pourrez notamment réviser et vous entraînez sur les chapitres suivants :

Si vous souhaitez accéder à l’ensemble des méthodes et aux corrigés des exemples, n’hésitez pas à télécharger l’application PrepApp

Cours et méthodes sur les équivalents en Maths Spé

1. Équivalents usuels et classiques en prépa Maths spé

PROF DE MATHS PARTICULIER

Des cours de qualité et enseignants aguerris

Préparer des concours ou s'exercer

2. Opérations autorisées sur les équivalents en MP, MPI, PC, PSI, PT

3. Opérations interdites sur les équivalents

4 – Des méthodes pour obtenir des équivalents usuels

PROF DE MATHS PARTICULIER

Des cours de qualité et enseignants aguerris

Préparer des concours ou s'exercer

Contact

Qui sommes-nous ?

Nous rejoindre

Copyright @ GROUPE REUSSITE - Mentions légales