Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Les séries numériques en Maths Spé
Résumé de cours Exercices et corrigés
Résumé de cours – séries numériques en MP, PC, MPI, PSI et PT
Ce chapitre débuté en classe de maths sup est très important pour les concours. Les notions travaillées dans ce chapitre vous serviront dans de nombreux chapitres en classe de MP, MPI, PSI, PT et PC. N’hésitez pas à faire appel à nos cours de maths à domicile si vous souhaitez maitriser complètement ces notions et viser les meilleures écoles d’ingénieurs aux concours.
1. Comment démontrer qu’une série à termes positifs converge ?
M1. Si 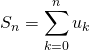 , montrer que la suite
, montrer que la suite ![]() des sommes partielles est majorée
des sommes partielles est majorée
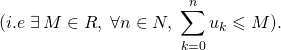
M2. Montrer qu’il existe une série de terme général ![]() positif ou nul convergente telle que
positif ou nul convergente telle que
![]() M2.1.
M2.1. ![]()
ou ![]() .
.
![]() M2.2. Montrer qu’il existe une suite
M2.2. Montrer qu’il existe une suite ![]() telle que pour
telle que pour ![]() assez grand,
assez grand, ![]() et telle que la série de terme général
et telle que la série de terme général ![]() converge.
converge.
![]() M2.3. Montrer que
M2.3. Montrer que ![]() où
où ![]() .
.
Pour cela, il suffit que ![]() où
où ![]() .
.
Cette méthode est souvent utilisable pour les séries de terme général de la forme ![]() (en prenant en général
(en prenant en général ![]() ), mais attention à ne pas passer à côté d’une série géométrique dans le cas
), mais attention à ne pas passer à côté d’une série géométrique dans le cas ![]() .
.
M3. Trouver une suite ![]() à termes positifs telle que
à termes positifs telle que ![]() , la série de terme général
, la série de terme général ![]() étant convergente.
étant convergente.
![]() M3.B. Montrer que
M3.B. Montrer que ![]() où
où ![]() .
.
![]() M4. Appliquer la règle d’Alembert.
M4. Appliquer la règle d’Alembert.
Trouver ![]() tel que pour tout
tel que pour tout ![]() ,
, ![]() et montrer que la suite
et montrer que la suite ![]() converge vers
converge vers ![]() vérifiant
vérifiant ![]()
Astuce : Il sera plus simple d’utiliser la règle de d’Alembert si vous avez auparavant trouvé un équivalent simple de ![]() ne contenant que des produits ou quotients.
ne contenant que des produits ou quotients.
M5. Montrer que ![]() où
où ![]() est une fonction continue sur
est une fonction continue sur ![]() où
où ![]() , décroissante, à valeurs positives ou nulles, et montrer que la suite de terme général
, décroissante, à valeurs positives ou nulles, et montrer que la suite de terme général ![]() converge.
converge.
M6. Montrer que ![]() où
où ![]() est une fonction continue sur
est une fonction continue sur ![]() (où
(où ![]() ), décroissante, à valeurs positives ou nulles et intégrable sur
), décroissante, à valeurs positives ou nulles et intégrable sur ![]() . (dans le chapitre intégration sur un intervalle quelconque).
. (dans le chapitre intégration sur un intervalle quelconque).
UN PROF DE MATHS POUR EXCELLER
La pratique et la compréhension
clés de la réussite
Cours de maths en ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
2. Comment démontrer qu’une série à termes positifs diverge ?
M1. Montrer que la suite ![]() ne converge pas vers 0.
ne converge pas vers 0.
M2. Montrer que la suite des sommes partielles ![]() n’est pas majorée.
n’est pas majorée.
M3. Montrer qu’il existe une suite ![]() à valeurs positives ou nulles telle que
à valeurs positives ou nulles telle que ![]() , la série de terme général
, la série de terme général ![]() étant divergente.
étant divergente.
![]() M3.B. Montrer qu’il existe une suite
M3.B. Montrer qu’il existe une suite ![]() telle que pour
telle que pour ![]() assez grand,
assez grand, ![]() , la série de terme général
, la série de terme général ![]() étant divergente.
étant divergente.
![]() M3.T. Montrer que
M3.T. Montrer que ![]() où
où ![]() . Il suffit pour cela que
. Il suffit pour cela que ![]() où
où ![]() ou
ou ![]()
M4. Trouver une suite ![]() à termes strictement positifs telle que
à termes strictement positifs telle que ![]() , la série de terme général
, la série de terme général ![]() étant divergente.
étant divergente.
![]() M4.B Montrer que
M4.B Montrer que ![]() où
où ![]()
M5. Appliquer la règle de d’Alembert trouver ![]() tel que pour tout
tel que pour tout ![]() ,
, ![]() et montrer que la suite
et montrer que la suite
![]() admet une limite
admet une limite ![]() strictement supérieure à 1 (la série est alors grossièrement divergente).
strictement supérieure à 1 (la série est alors grossièrement divergente).
M6. Montrer que ![]() où
où ![]() est une fonction continue sur
est une fonction continue sur ![]() où
où ![]() , décroissante, à valeurs positives ou nulles, et montrer que la suite de terme général
, décroissante, à valeurs positives ou nulles, et montrer que la suite de terme général ![]() diverge. (exemple de cas d’application: série de terme général
diverge. (exemple de cas d’application: série de terme général ![]() ).
).
M7. Montrer que ![]() où
où ![]() est une fonction continue sur
est une fonction continue sur ![]() (où
(où ![]() ), décroissante, à valeurs positives ou nulles et non intégrable sur
), décroissante, à valeurs positives ou nulles et non intégrable sur ![]() . (dans le chapitre intégration sur un intervalle quelconque).
. (dans le chapitre intégration sur un intervalle quelconque).
3. Comment démontrer qu’une série à termes quelconques converge ?
M1. Montrer qu’elle est absolument convergente c’est-à-dire appliquer à la série de terme général ![]() l’un des critères du
l’un des critères du ![]() .
.
M2. Trouver une suite ![]() convergente telle que
convergente telle que ![]() et appliquer le critère de comparaison suite-série.
et appliquer le critère de comparaison suite-série.
M3. Effectuer le DL de ![]() à l’ordre deux en
à l’ordre deux en ![]() .
.
Lorsque l’on obtient ![]() , la série est convergente si, et seulement si,
, la série est convergente si, et seulement si, ![]() (à justifier).
(à justifier).
Lorsque l’on obtient ![]() , la série est convergente si, et seulement si,
, la série est convergente si, et seulement si, ![]() (à justifier).
(à justifier).
M4. Montrer qu’elle vérifie le théorème spécial des séries alternées.
Lorsque ![]()
![]() ou
ou ![]()
![]() , avec
, avec ![]() , pour démontrer que la suite
, pour démontrer que la suite ![]() est décroissante, il suffit de trouver une fonction
est décroissante, il suffit de trouver une fonction ![]() telle que
telle que ![]() et de prouver que la fonction
et de prouver que la fonction ![]() est décroissante sur
est décroissante sur ![]() ou sur
ou sur ![]() pour
pour ![]()
M5. Lorsque ![]() est équivalent au terme général
est équivalent au terme général ![]() d’une série alternée convergente, écrire
d’une série alternée convergente, écrire
![]() ,
,
Trouver la valeur de ![]() ou un équivalent simple de
ou un équivalent simple de ![]() qui permette de dire si la série de terme général
qui permette de dire si la série de terme général ![]() converge ou diverge.
converge ou diverge.
L’équivalence ![]() et la convergence de
et la convergence de ![]() n’impliquent pas la convergence de
n’impliquent pas la convergence de ![]() .
.
Exemple : ![]() vérifie
vérifie ![]() .
.
![]() converge si
converge si ![]() et diverge si
et diverge si ![]() .
.
M6. Utiliser un groupement par paquets .
On suppose que la suite ![]() converge vers 0.
converge vers 0.
![]() Montrer que la série de terme général
Montrer que la série de terme général ![]() converge.
converge.
Montrer enfin que les suites ![]() et
et ![]() convergent vers la même limite
convergent vers la même limite ![]() .
.
(![]() est la somme partielle d’ordre
est la somme partielle d’ordre ![]() de la série de terme général
de la série de terme général ![]() ).
).
![]() Montrer que la série de terme général
Montrer que la série de terme général ![]() converge.
converge.
Montrer enfin que les suites ![]() ,
, ![]() et
et ![]() convergent vers la même limite
convergent vers la même limite ![]() .
.
(![]() est la somme partielle d’ordre
est la somme partielle d’ordre ![]() de la série de terme général
de la série de terme général ![]() ).
).
Alors la série de terme général ![]() converge.
converge.
M7. Pour une série de terme général ![]() , après s’être assuré que la série n’est pas absolument convergente ou que l’intégrale n’est pas facilement calculable, on peut chercher à démontrer qu’elle vérifie le théorème spécial des séries alternées :
, après s’être assuré que la série n’est pas absolument convergente ou que l’intégrale n’est pas facilement calculable, on peut chercher à démontrer qu’elle vérifie le théorème spécial des séries alternées :
Ce qui sera vrai si ![]() est continue sur
est continue sur ![]() , décroissante et de limite nulle en
, décroissante et de limite nulle en ![]() , le changement de variable
, le changement de variable
![]() permet d’obtenir la forme
permet d’obtenir la forme
![]()
Pour optimiser vos révisions et vous aider à rédiger vos fiches de révision, n’hésitez pas à vous rendre sur les cours en ligne mis à disposition des étudiants en Maths Spé. Vous pourrez ainsi accéder aux cours en ligne de MP en maths, à différents cours en ligne de PC en Maths, aux cours en ligne de PT en Maths, mais également à des cours en ligne de Maths en PSI.
4 – Comment démontrer la divergence d’une série à termes quelconques ?
Remarque : si ![]() garde un signe constant pour
garde un signe constant pour ![]() assez grand, on peut utiliser le paragraphe II- en raisonnant avec
assez grand, on peut utiliser le paragraphe II- en raisonnant avec ![]() ou avec
ou avec ![]() .
.
M1. Si la suite ![]() ne converge pas vers 0, la série de terme général
ne converge pas vers 0, la série de terme général ![]() diverge grossièrement.
diverge grossièrement.
M2. Si pour tout ![]() ,
, ![]() et si la suite de terme général
et si la suite de terme général ![]() admet une limite
admet une limite ![]() , la série
, la série ![]() diverge grossièrement.
diverge grossièrement.
M3. Si ![]() où la suite de terme général
où la suite de terme général ![]() diverge, la série de terme général
diverge, la série de terme général ![]() diverge.
diverge.
COURS DE MATHS
Nous avons recruté pour vous les meilleurs professeurs particuliers de maths
S'EXERCER ET APPRENDRE
Avis Google France ★★★★★ 4,8 sur 5
5. Comment calculer la somme d’une série numérique ?
M1. Calcul par télescopage :
![]() Si l’on peut écrire
Si l’on peut écrire
![]() ,
,
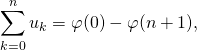 il suffit de connaître
il suffit de connaître ![]() pour calculer la somme de la série.
pour calculer la somme de la série.
![]() Si l’on peut écrire
Si l’on peut écrire ![]() ,
,
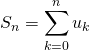 est égal à
est égal à ![]() ,
,
il suffit de connaître ![]() ou
ou ![]() pour trouver la somme de la série.
pour trouver la somme de la série.
M2. Pour calculer la somme d’une série de terme général ![]() où
où ![]() est une fonction polynôme et où
est une fonction polynôme et où 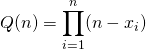 avec
avec ![]() deux à deux distincts.
deux à deux distincts.
Lorsque la série converge,
![]() chercher des scalaires
chercher des scalaires ![]() tels que
tels que 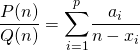
(cette décomposition en éléments simples est obtenue par expand avec une TI formelle ou par utilisation du cours de MPSI).
![]() puis regarder s’il est possible par groupements de termes d’obtenir
puis regarder s’il est possible par groupements de termes d’obtenir ![]() de la forme
de la forme
![]() ou
ou ![]()
![]() Lorsque
Lorsque ![]() s’exprime en fonction de
s’exprime en fonction de
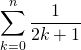 ou même de
ou même de ![]() ,
,
on exprime ces sommes en fonction de la suite ![]() telle que
telle que
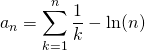 et on utilise la convergence de
et on utilise la convergence de ![]() vers la constante d’Euler
vers la constante d’Euler ![]() .
.
M3. Pour une série dont le terme général ![]() s’écrit
s’écrit ![]() , où
, où ![]() est une fonction polynôme de degré
est une fonction polynôme de degré ![]() ,
,
décomposer ![]() dans la base de polynômes étagés
dans la base de polynômes étagés ![]()
![]() et simplifier, pour
et simplifier, pour ![]() ,
,
![]()
M4. Utiliser les séries connues :
![]() Si
Si ![]() ,
, ![]()
![]()
![]() si
si ![]()
![]() ;
;
![]()
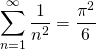
![]()
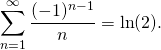
M5.A. Pour une série dont le terme général est de la forme
![]() ,
,
calculer la somme partielle ![]()
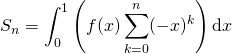
![]()
![]()
avec ![]()
et démontrer que ![]() converge vers 0 en utilisant
converge vers 0 en utilisant ![]() si pour tout
si pour tout ![]() ,
, ![]() .
.
M5.B. Pour une série dont le terme général est de la forme
![]() ,
,
![]() montrer que la fonction
montrer que la fonction ![]() est continue sur
est continue sur ![]() ,
,
![]() écrire la somme partielle
écrire la somme partielle ![]() d’ordre
d’ordre ![]() sous la forme :
sous la forme :
![]()
où ![]()
![]() et démontrer que
et démontrer que ![]() converge vers 0 en utilisant
converge vers 0 en utilisant ![]() si pour tout
si pour tout ![]() ,
, ![]()
M6. Pour une série dont le terme général est de la forme ![]() , on pourra aussi
, on pourra aussi
![]() chercher à démontrer que la série de fonctions de terme général
chercher à démontrer que la série de fonctions de terme général ![]() converge uniformément sur
converge uniformément sur ![]() , pour pouvoir intervertir la somme de la série et l’intégrale (chapitre suites et séries de fonctions en MP, PSI, MPI, PC et PT)
, pour pouvoir intervertir la somme de la série et l’intégrale (chapitre suites et séries de fonctions en MP, PSI, MPI, PC et PT)
![]() ou chercher à appliquer le théorème d’interversion du signe somme et de l’intégrale (chapitre intégration sur un intervalle quelconque).
ou chercher à appliquer le théorème d’interversion du signe somme et de l’intégrale (chapitre intégration sur un intervalle quelconque).
M7. Reconnaître un produit de Cauchy.
Pour cela, il suffit de trouver deux séries absolument convergentes ![]() et
et ![]() et de vérifier que
et de vérifier que 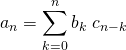 .
.
Par théorème, ![]() converge absolument et
converge absolument et
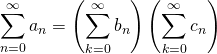 .👍 Conseil : rappelez la formule du produit de Cauchy, précisez les deux suites
.👍 Conseil : rappelez la formule du produit de Cauchy, précisez les deux suites ![]() ) et
) et ![]() et faites bien attention à la plage de sommation.
et faites bien attention à la plage de sommation.
En particulier si 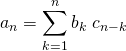 , on peut se ramener à un produit de Cauchy en posant
, on peut se ramener à un produit de Cauchy en posant ![]() .
.
Prenez de l’avance sur les cours dispensés en prépa en révisant maintenant les chapitres à venir dans le programme de maths en Maths Spé :
- Cours espaces vectoriels en MP, PC, PSI, PT et MPI
- Cours sur la réduction d’endomorphismes en maths spé
- Résumé de cours matrices en MP, MPI, PT, PSI, PC
- Cours sur les espaces vectoriels normés
- Résumé de cours suites et les séries de fonctions
Si vous souhaitez accéder à l’ensemble des méthodes et aux corrigés des exemples, n’hésitez pas à télécharger l’application PrepApp

