Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Cours Variables aléatoires MP, PC, PSI, PT
Résumé de cours Exercices et corrigés
Résumé de cours et méthodes – Variables aléatoires
1. Variables aléatoires discrètes
![]() 1. Pour démontrer que
1. Pour démontrer que ![]() est une variable aléatoire discrète sur
est une variable aléatoire discrète sur ![]()
![]() Il suffit de démontrer que
Il suffit de démontrer que
… ![]() est une application de
est une application de ![]() dans un ensemble
dans un ensemble ![]() .
.
… ![]() est une partie finie ou dénombrable de
est une partie finie ou dénombrable de ![]() .
.
… et ![]() ,
, ![]()
![]() Il suffit de prouver que
Il suffit de prouver que ![]() est une combinaison linéaire ou un produit d’un nombre fini de variables aléatoires discrètes réelles sur
est une combinaison linéaire ou un produit d’un nombre fini de variables aléatoires discrètes réelles sur ![]() .
.
![]() Il suffit de trouver une variable aléatoire discrète
Il suffit de trouver une variable aléatoire discrète ![]() sur
sur ![]() et une fonction
et une fonction ![]() définie sur
définie sur ![]() telles que
telles que ![]() .
.
![]() Il suffit de trouver
Il suffit de trouver ![]() variables aléatoires
variables aléatoires ![]() sur
sur ![]() et une fonction
et une fonction ![]() définie sur
définie sur 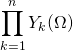 telles que
telles que ![]() .
.
![]() 2. Pour donner la loi d’une variable aléatoire discrète
2. Pour donner la loi d’une variable aléatoire discrète ![]() , on détermine
, on détermine ![]() et pour
et pour ![]() .
.
Il est conseillé si la loi de ![]() doit servir et si les calculs sont assez simples de prendre le temps de vérifier que la famille
doit servir et si les calculs sont assez simples de prendre le temps de vérifier que la famille ![]() est une famille sommable de somme égale à 1.
est une famille sommable de somme égale à 1.
![]() 3. Obtention d’un système complet d’événements
3. Obtention d’un système complet d’événements
![]() est un système complet d’événements.
est un système complet d’événements.
![]() 4. Pour démontrer que les variables aléatoires
4. Pour démontrer que les variables aléatoires ![]() et
et ![]() suivent la même loi, on démontre que
suivent la même loi, on démontre que
![]()
![]()
![]()
![]() .
.
Dans ce cas, si elles existent, ![]() et
et ![]() .
.
Cela ne veut pas dire que ![]() .
.
Voir aussi l’utilisation des fonctions génératrices lorsque ![]() et
et ![]() sont à valeurs dans
sont à valeurs dans ![]() .
.
![]() 5. Variables aléatoires suivant une loi binomiale
5. Variables aléatoires suivant une loi binomiale
![]() On peut justifier le fait que
On peut justifier le fait que ![]() suit une loi binomiale de paramètres
suit une loi binomiale de paramètres ![]() et
et ![]() en montrant que
en montrant que ![]() est le nombre de succès au cours de
est le nombre de succès au cours de ![]() épreuves identiques et indépendantes de Bernoulli de probabilité
épreuves identiques et indépendantes de Bernoulli de probabilité ![]() de « succès ».
de « succès ».
![]() On peut aussi justifier la loi binomiale en écrivant
On peut aussi justifier la loi binomiale en écrivant ![]() comme somme de
comme somme de ![]() variables aléatoires indépendantes, de même loi de Bernoulli de paramètre
variables aléatoires indépendantes, de même loi de Bernoulli de paramètre ![]() .
.
![]() 6. Variables aléatoires suivant une loi géométrique
6. Variables aléatoires suivant une loi géométrique
Lorsque l’on effectue une suite d’épreuves indépendantes et identiques de probabilité ![]() de « succès », la variable aléatoire égale au rang du premier succès suit une loi géométrique de paramètre
de « succès », la variable aléatoire égale au rang du premier succès suit une loi géométrique de paramètre ![]() .
.
![]() 7. Pour vérifier qu’une application
7. Pour vérifier qu’une application ![]() définit la loi d’une variable aléatoire discrète
définit la loi d’une variable aléatoire discrète
Il suffit de se donner un ensemble ![]() fini ou dénombrable et une fonction
fini ou dénombrable et une fonction ![]() de
de ![]() dans
dans ![]() telle que la famille
telle que la famille ![]() soit sommable de somme égale à 1.
soit sommable de somme égale à 1.
Alors il existe une variable aléatoire sur ![]() sur
sur ![]() telle que
telle que ![]() et
et ![]() .
.
Remarque : il est possible que ![]() ne soit définie que presque-sûrement c’est à dire que
ne soit définie que presque-sûrement c’est à dire que ![]() soit seulement un système quasi-complet d’événements.
soit seulement un système quasi-complet d’événements.
C’est le cas pour ![]() de loi géométrique égale au temps d’arrêt pour obtenir pour la première fois un événement
de loi géométrique égale au temps d’arrêt pour obtenir pour la première fois un événement ![]() de probabilité
de probabilité ![]() , la probabilité de ne jamais obtenir l’événement
, la probabilité de ne jamais obtenir l’événement ![]() étant nulle.
étant nulle.
PROF DE MATHS PARTICULIER
Des cours de qualité et enseignants aguerris
Préparer des concours ou s'exercer
Avis Google France ★★★★★ 4,9 sur 5
2. Couples de variables aléatoires
2.1. Loi d’un couple et lois marginales
![]() 1. Pour donner la loi d’un couple
1. Pour donner la loi d’un couple ![]() de variables discrètes, il faut donner :
de variables discrètes, il faut donner : ![]() et pour tout
et pour tout ![]() et
et ![]() , la valeur de
, la valeur de ![]() .
.
![]() On peut noter aussi :
On peut noter aussi : ![]()
![]() Faire apparaître clairement les conditions sur
Faire apparaître clairement les conditions sur ![]() et
et ![]() lorsque
lorsque ![]() dépend des positions relatives de
dépend des positions relatives de ![]() et
et ![]() .
.
![]() Lorsque
Lorsque ![]() et
et ![]() sont de cardinal peu élevé, on peut présenter les résultats en un tableau à double entrée.
sont de cardinal peu élevé, on peut présenter les résultats en un tableau à double entrée.
La famille ![]() est sommable de somme égale à 1.
est sommable de somme égale à 1.
![]() 2. Ayant la loi du couple
2. Ayant la loi du couple ![]() , on en déduit les lois marginales par sommation.
, on en déduit les lois marginales par sommation.
![]()
![]() .
.
![]()
![]() .
.
La seule difficulté est de tenir compte des conditions liant ![]() et
et ![]() s’il y en a.
s’il y en a.
![]() 3.
3. ![]() La donnée des lois marginales de
La donnée des lois marginales de ![]() et
et ![]() ne donne pas la loi du couple sauf si les variables
ne donne pas la loi du couple sauf si les variables ![]() et
et ![]() sont indépendantes.
sont indépendantes.
![]() Il est possible d’avoir des couples
Il est possible d’avoir des couples ![]() et
et ![]() ayant des lois conjointes différentes, alors que les lois marginales sont les mêmes.
ayant des lois conjointes différentes, alors que les lois marginales sont les mêmes.
![]() Si
Si ![]() et
et ![]() suivent des lois de Bernoulli de paramètres connus et si l’on connaît une des 4 probabilités
suivent des lois de Bernoulli de paramètres connus et si l’on connaît une des 4 probabilités
![]() avec
avec ![]() et
et ![]() dans
dans ![]() , on peut trouver la loi du couple
, on peut trouver la loi du couple ![]() .
.
2.2. Indépendance de deux variables aléatoires
![]() 1. Pour étudier l’indépendance des variables
1. Pour étudier l’indépendance des variables ![]() et
et ![]() ,
,
a) s’il existe ![]() et
et ![]() tels que
tels que ![]() alors que
alors que ![]() , les variables
, les variables ![]() et
et ![]() ne sont pas indépendantes.
ne sont pas indépendantes.
b) s’il existe ![]() et
et ![]() tels que
tels que ![]() les variables
les variables ![]() et
et ![]() ne sont pas indépendantes.
ne sont pas indépendantes.
c) si l’on ne trouve pas de telles valeurs, pour démontrer l’indépendance, on doit vérifier que
![]() ,
, ![]()
![]() 2. Si
2. Si ![]() et
et ![]() sont des variables aléatoires indépendantes, pour tout
sont des variables aléatoires indépendantes, pour tout ![]() et
et ![]() ,
, ![]() et
et ![]() sont des événements indépendants.
sont des événements indépendants.
Ce résultat est souvent utilisé sous la forme :
Si ![]() et
et ![]() sont des variables aléatoires réelles indépendantes, pour tous intervalles
sont des variables aléatoires réelles indépendantes, pour tous intervalles ![]() et
et ![]() de
de ![]() , les événements
, les événements ![]() et
et ![]() sont indépendants.
sont indépendants.
![]() 3. Si
3. Si ![]() et
et ![]() sont indépendantes et ont une espérance mathématique,
sont indépendantes et ont une espérance mathématique, ![]() a une espérance et
a une espérance et ![]()
donc la covariance de ![]() et
et ![]() est nulle. La réciproque est fausse.
est nulle. La réciproque est fausse.
![]() 4. Si
4. Si ![]() et
et ![]() sont indépendantes et si
sont indépendantes et si ![]() (resp.
(resp. ![]() ) est une application définie sur
) est une application définie sur ![]() (resp.
(resp. ![]() ),
), ![]() et
et ![]() sont des variables indépendantes.
sont des variables indépendantes.
COURS DE MATHS A DOMICILE
Les meilleurs profs de maths pour
réussir sa scolarité
En ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
3. Indépendance mutuelle de  variables aléatoires
variables aléatoires
![]() 1.
1. ![]() sont des variables aléatoires discrètes mutuellement indépendantes lorsque
sont des variables aléatoires discrètes mutuellement indépendantes lorsque
![]()
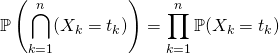 .
.
![]() 2. Si
2. Si ![]() sont des variables aléatoires discrètes mutuellement indépendantes,
sont des variables aléatoires discrètes mutuellement indépendantes,
![]() elles sont 2 à 2 indépendantes.
elles sont 2 à 2 indépendantes.
![]() si
si ![]() ,
, ![]() est une application définie sur
est une application définie sur ![]() ,
, ![]() sont des variables aléatoires discrètes mutuellement indépendantes.
sont des variables aléatoires discrètes mutuellement indépendantes.
![]() si
si ![]() et si
et si ![]() est une application définie sur
est une application définie sur ![]() et
et ![]() est définie sur
est définie sur ![]() , les variables
, les variables ![]() et
et ![]() sont indépendantes.
sont indépendantes.
Dans la suite, on suppose de plus que les variables aléatoires sont réelles.
![]() Si
Si ![]() ,
, ![]() est un intervalle de
est un intervalle de ![]() les événements
les événements ![]() sont mutuellement indépendants.
sont mutuellement indépendants.
![]()
![]() et
et ![]() sont des variables aléatoires indépendantes.
sont des variables aléatoires indépendantes.
(lemme des coalitions)
Les cours de mathématiques en Maths Spé doivent être appris rigoureusement, et les définitions de cours ainsi que les méthodes de cours doivent être apprises par cœur. Chaque cours comme les cours en ligne de Maths en PT, par exemple ou les cours en ligne de Maths en MP, les cours en ligne de Maths en PSI et les cours en ligne de Maths en PC comportent ces notions essentielles qui guideront les étudiants vers la réussite.
4. Recherche de lois particulières
4.1. Maximum et minimum de 2 variables aléatoires réelles
Si ![]() et
et ![]() sont deux variables et
sont deux variables et ![]() et
et ![]() ,
,
![]() Lois de
Lois de ![]() et
et ![]()
![]()
![]()
![]() .
.
![]()
![]() ,
,
![]()
![]()
![]() .
.
![]() Loi du couple
Loi du couple
![]()
![]()
![]()
![]() .
.
![]() Si
Si ![]() ,
, ![]()
![]()
![]()
![]() et si
et si ![]() .
.
On peut aussi utiliser la méthode du paragraphe suivant.
👍 Il est utile de se souvenir des relations : ![]() et
et ![]() .
.
4.2. Maximum et minimum de ![]() variables aléatoires réelles
variables aléatoires réelles
Si ![]() sont
sont ![]() variables aléatoires réelles, on note
variables aléatoires réelles, on note ![]() et
et ![]() .
.
![]() Loi de
Loi de ![]()
On calcule 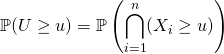
(On peut aussi utiliser ![]() ).
).
Lorsque les variables ![]() sont à valeurs dans
sont à valeurs dans ![]() , on utilise si
, on utilise si ![]()
![]() donc
donc
![]()
![]() Loi de
Loi de ![]()
On calcule 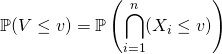 .
.
Lorsque les variables ![]() sont à valeurs dans
sont à valeurs dans ![]() , on utilise si
, on utilise si ![]()
![]() donc
donc
![]() et
et ![]() .
.
![]() Loi du couple
Loi du couple ![]()
On détermine lorsque ![]() ,
, 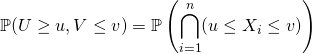
4.3. Utilisation de relations matricielles
Soit ![]() .
. ![]() une partie non vide de
une partie non vide de ![]() formée d’éléments consécutifs (en général
formée d’éléments consécutifs (en général ![]() ou
ou ![]() ).
).
On suppose que l’on définit une famille (finie ou infinie) de variables aléatoires ![]() à valeurs dans
à valeurs dans ![]() telles que
telles que ![]() tel que
tel que ![]() ,
, ![]()
(![]() est indépendant de
est indépendant de ![]() ).
).
On introduit la matrice ![]()
Soit ![]() .
.
On vérifie que ![]() .
.
Dans le cas où ![]() , on obtient pour tout entier
, on obtient pour tout entier ![]() ,
, ![]() , il faudra déterminer la matrice
, il faudra déterminer la matrice ![]() (en la diagonalisant par exemple).
(en la diagonalisant par exemple).
Propriétés de ![]() et de sa transposée.
et de sa transposée.
![]() a) La somme des termes de chaque colonne de
a) La somme des termes de chaque colonne de ![]() est égale à 1.
est égale à 1.
![]() b)
b) ![]() admet 1 pour valeur propre et le vecteur de coordonnées égales à 1 est un vecteur propre de
admet 1 pour valeur propre et le vecteur de coordonnées égales à 1 est un vecteur propre de ![]() associé à la valeur propre 1
associé à la valeur propre 1
![]() c) 1 est toujours valeur propre de la matrice
c) 1 est toujours valeur propre de la matrice ![]() (puisque 1 est valeur propre de
(puisque 1 est valeur propre de ![]() ). On peut démontrer que les autres valeurs propres de
). On peut démontrer que les autres valeurs propres de ![]() sont de module inférieur ou égal à 1.
sont de module inférieur ou égal à 1.
Voir aussi le paragraphe 5 chaînes de Markov (méthodes probabilités), pour déterminer la limite de la suite ![]() lorsque
lorsque ![]() .
.
4.5. Loi de la différence de deux variables aléatoires à valeurs dans ![]()
Soient ![]() et
et ![]() deux variables aléatoires à valeurs dans
deux variables aléatoires à valeurs dans ![]() .
.
On utilise si ![]() ,
, 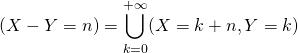
et 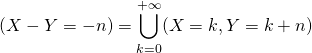
Dans les deux cas, on a introduit une réunion dénombrable d’événements 2 à 2 incompatibles.
Il est conseillé de calculer ![]() si
si ![]() plutôt que
plutôt que ![]() pour
pour ![]() .
.
On raisonne comme dans le paragraphe précédent, avec les mêmes précautions dans les calculs pratiques.
Par contre, il est impossible d’utiliser la fonction génératrice de ![]() sauf si
sauf si ![]() .
.
Il est conseillé de calculer ![]() si
si ![]() plutôt que
plutôt que ![]() pour
pour ![]() .
.
On raisonne comme dans le paragraphe précédent, avec les mêmes précautions dans les calculs pratiques.
Par contre, il est impossible d’utiliser la fonction génératrice de ![]() sauf si
sauf si ![]() .
.
Délaisser les révisions de certains chapitres de maths est une mauvaise stratégie de révision. En effet, pour obtenir de bonnes notes lors des épreuves de concours, il est primordial de s’assurer d’avoir un niveau de connaissances homogène dans tous les chapitres du programme. Si ce n’est pas le cas, utilisez un cours particulier de maths en ligne pour améliorer votre niveau, et révisez :

