Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Algèbre linéaire et matrices pour les MP, PC, PSI et PT
Résumé de cours et exercices corrigés
Résumé de cours et méthodes – algèbre linéaire et matrices
1. Sous espaces vectoriels d’un e.v. de dimension 3
Dans toute cette partie, ![]() est un
est un ![]() – espace vectoriel de dimension 3 de base
– espace vectoriel de dimension 3 de base ![]() .
.
Exercice 1.
Soit ![]() le sous espace vectoriel
le sous espace vectoriel
![]() .
.
1. Trouver une base de ![]()
2. Trouver une base pour ![]()
3. On rappelle que ![]()
![]() et que
et que ![]() .
.
Trouver une base de ![]()
4. Montrer que ![]()
2. S.e.v. et supplémentaire
Soit ![]() dont la base canonique est notée
dont la base canonique est notée ![]() .
.
Soit ![]() l’ensemble
l’ensemble
![]()
et ![]() .
.
Question 1
Quel est la dimension de l’espace vectoriel ![]() ?
?
Question 2
On rappelle que ![]() est égal à
est égal à
![]()
et ![]()
et que ![]() est la base canonique.
est la base canonique.
Quel est le couple de vecteurs qui n’engendre pas un supplémentaire de ![]()
3. Exemples d’espaces vectoriels d’applications
On se place dans l’espace vectoriel ![]() des applications dérivables de
des applications dérivables de ![]() dans
dans ![]() .
.
Premier exemple
On note ![]() :
: ![]() ,
,
![]() :
: ![]()
et ![]() :
: ![]() .
.
La famille ![]() est-elle une famille libre ?
est-elle une famille libre ?
Deuxième exemple
Soit ![]() :
: ![]()
![]() :
: ![]()
![]() :
: ![]() .
.
La famille ![]() est-elle une famille libre ?
est-elle une famille libre ?
Pour encore plus de cours en ligne gratuits et accessibles directement depuis votre ordinateur ou smartphone, rendez-vous dès maintenant sur la page de cours en ligne de Maths en MP, la page des cours en ligne de Maths en PSI mais aussi sur la page de cours en ligne de Maths en PC et sur la page des cours en ligne de Maths en PT. Vous pouvez, de plus, retrouvez nos cours de soutien en maths pour réussir en prépa scientifique.
4. Recherche d’image et de noyau
Soit ![]() l’endomorphisme de
l’endomorphisme de ![]() canoniquement associé à
canoniquement associé à
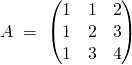 .
.
Question 1
Quel est le rang de ![]() ?
?
Question 2 : Image de ![]()
Une base de ![]() est égale à
est égale à
Question 3 : Noyau de ![]()
Une base de ![]() est
est ![]() pour
pour ![]()
Question 4
![]() a pour équation dans la base canonique
a pour équation dans la base canonique ![]()
5. Étude d’une matrice de projecteur
Question 1
L’ endomorphisme ![]() canoniquement associé à la matrice
canoniquement associé à la matrice
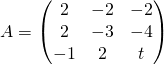
est un projecteur pour ![]() ?
?
On suppose dans la suite que ![]() est la matrice d’un projecteur
est la matrice d’un projecteur ![]() dans la base canonique de
dans la base canonique de ![]() .
.
Question 2
Pour déterminer ![]() , on résout l’équation
, on résout l’équation ![]() ?
?
Question 3
Pour déterminer une base de ![]() , on résout l’équation
, on résout l’équation ![]() ?
?
Question 4
![]() est le plan d’équation
est le plan d’équation ![]() où
où ![]() ?
?
Question 5 : (suite des questions 3 et 4)
![]() est une base de
est une base de ![]() dans laquelle la matrice de
dans laquelle la matrice de ![]() est une matrice diagonale ?
est une matrice diagonale ?
Si l’affirmation est vraie, donner cette matrice diagonale.
Question 6
Montrer que la matrice de passage de la base canonique à la base ![]() est
est
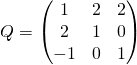
et ![]() .
.
COURS DE MATHS A DOMICILE
Les meilleurs profs de maths pour
réussir sa scolarité
En ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
Corrigés des exercices sur les espaces vectoriels en maths spé
Exercice 1 :
1. Méthode :
![]() est l’équation d’un plan
est l’équation d’un plan ![]() dans un espace vectoriel de dimension 3 par rapport à une base donnée.
dans un espace vectoriel de dimension 3 par rapport à une base donnée.
On tire l’une des inconnues en fonction des autres, on remplace dans le vecteur générique de ![]() que l’on ordonne en fonction des inconnues conservées ; les deux vecteurs ainsi obtenus en coefficients de ces inconnues forment une base du plan.
que l’on ordonne en fonction des inconnues conservées ; les deux vecteurs ainsi obtenus en coefficients de ces inconnues forment une base du plan.
On généralise cette méthode dans le cas d’un hyperplan ![]() d’équation
d’équation ![]() dans un espace vectoriel de dimension
dans un espace vectoriel de dimension ![]() .
.
Calcul :
![]() est un plan donné par son équation dans la base
est un plan donné par son équation dans la base ![]() ,
,
donc ![]()
![]()
![]()
![]()
![]()
où ![]() et
et ![]() .
.
![]() est une famille génératrice formée de deux vecteurs non colinéaires, c’est une base de
est une famille génératrice formée de deux vecteurs non colinéaires, c’est une base de ![]() .
.
⚠️ On peut démontrer par contre que
Vect![]() est un supplémentaire de
est un supplémentaire de ![]() .
.
Pour cela, puisque ![]() est un plan de
est un plan de ![]() , il suffit de prouver que
, il suffit de prouver que ![]()
⚠️ On fera attention à ne pas confondre le vecteur ![]() et les coordonnées
et les coordonnées ![]() .
.
Pour qu’il y ait égalité, il faut que ![]() soit égal à
soit égal à ![]() et que
et que ![]() soit la base canonique de
soit la base canonique de ![]() .
.
2. ![]()
![]()
![]()
où ![]() et
et ![]() .
.
![]() est une famille génératrice du plan
est une famille génératrice du plan ![]() formée de deux vecteurs non colinéaires, c’est une base de
formée de deux vecteurs non colinéaires, c’est une base de ![]() .
.
3. On cherche ![]() vérifiant le système :
vérifiant le système :
![]()
![]()
![]()
On obtient ![]() et on obtient une base en prenant
et on obtient une base en prenant ![]() soit
soit ![]() .
.
4.Par la formule de Grassmann,
![]()
![]()
donc ![]() .
.
La Maths Spé est la dernière ligne droite avant l’intégration des meilleures écoles d’ingénieurs françaises. Pour maximiser vos chances de réussite, continuez vos révisions avec les autres chapitres au programme de MP, PC et PSI, dont :

