Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Dénombrements en MP, PC, PSI et PT
Résumé de cours Exercices et corriges
Exercices et corrigés – Dénombrements
1. Ensembles dénombrables
Exercice 1 :
Soit ![]() une fonction croissante de
une fonction croissante de ![]() dans
dans ![]() . Montrer que l’ensemble des points de discontinuité de
. Montrer que l’ensemble des points de discontinuité de ![]() est au plus dénombrable.
est au plus dénombrable.
Corrigé de l’exercice 1 :
Soit ![]() l’ensemble des points de discontinuité de
l’ensemble des points de discontinuité de ![]() .
.
En tout point ![]() ,
, ![]() admet une limite à gauche
admet une limite à gauche ![]() et une limite à droite
et une limite à droite ![]() telles que
telles que ![]() .
.
![]() étant dense dans
étant dense dans ![]() , il existe
, il existe ![]() tel que
tel que ![]() .
.
On définit ainsi une application ![]() injective.
injective.
Comme ![]() est dénombrable, il existe une bijection
est dénombrable, il existe une bijection ![]() de
de ![]() sur
sur ![]() donc une injection
donc une injection ![]() de
de ![]() dans
dans ![]() .
.
On en déduit que ![]() est finie ou dénombrable.
est finie ou dénombrable.
Exercice 2 :
Soit ![]() l’ensemble des suites d’éléments égaux à
l’ensemble des suites d’éléments égaux à ![]() ou
ou ![]() .
.
Question 1
![]() est dénombrable ?
est dénombrable ?
Question 2
On note ![]() l’ensemble des éléments de
l’ensemble des éléments de ![]() qui sont des
qui sont des ![]() à partir d’un certain rang.
à partir d’un certain rang.
![]() est dénombrable ?
est dénombrable ?
Question 3
L’ensemble ![]() des suites périodiques de
des suites périodiques de ![]() est dénombrable ?
est dénombrable ?
Corrigé de l’exercice 2 :
Question 1 :
On définit alors la suite
On obtient un élément
Question 2
On note ![]() ,
, ![]()
et si ![]() l’ensemble des éléments de
l’ensemble des éléments de ![]() dont le terme d’indice
dont le terme d’indice ![]() est égal à 1, les termes d’indices supérieurs ou égaux à
est égal à 1, les termes d’indices supérieurs ou égaux à ![]() sont des
sont des ![]() .
.
L’application ![]()
![]() est bijective.
est bijective.
Comme ![]() est fini,
est fini, ![]() est fini.
est fini.
![]() est la réunion dénombrable des ensembles finis
est la réunion dénombrable des ensembles finis ![]() et de l’ensemble
et de l’ensemble ![]() , donc
, donc ![]() est fini ou dénombrable.
est fini ou dénombrable.
![]() contient une famille infinie :
contient une famille infinie : ![]() où
où ![]() est la suite formée de
est la suite formée de ![]()
![]() suivis de
suivis de ![]() .
.
Donc ![]() est dénombrable.
est dénombrable.
Question 3
On note ![]() l’ensemble des éléments de
l’ensemble des éléments de ![]() périodiques de période
périodiques de période ![]() .
.
Si ![]() , à tout élément
, à tout élément ![]() de
de ![]() on associe l’élément de
on associe l’élément de ![]() égal à
égal à ![]() .
.
On définit ainsi une application bijective de ![]() dans
dans ![]() car une suite périodique de période
car une suite périodique de période ![]() est entièrement définie par ses
est entièrement définie par ses ![]() premiers éléments.
premiers éléments.
![]()
![]() est une réunion dénombrable d’ensembles finis, donc
est une réunion dénombrable d’ensembles finis, donc ![]() est fini ou dénombrable.
est fini ou dénombrable.
![]() contient une famille infinie à savoir la famille
contient une famille infinie à savoir la famille ![]() où
où ![]() est la suite périodique de période
est la suite périodique de période ![]() dont les
dont les ![]() premiers éléments sont
premiers éléments sont ![]()
(![]() éléments
éléments ![]() suivis de
suivis de ![]() ).
).
Donc ![]() est dénombrable.
est dénombrable.
Exercice 3 :
Question 1
Montrer que l’ensemble des parties finies de ![]() est dénombrable.
est dénombrable.
Question 2
L’ensemble des parties de ![]() n’est pas dénombrable ?
n’est pas dénombrable ?
Corrigé de l’exercice 3 :
Question 1 :
On note ![]() l’ensemble des parties finies non vides de
l’ensemble des parties finies non vides de ![]() .
.
On note ![]() l’ensemble des parties finies de
l’ensemble des parties finies de ![]() de cardinal
de cardinal ![]() .
.
![]() Première méthode
Première méthode
On considère ![]() (les
(les ![]() étant rangés par ordre strictement croissant).
étant rangés par ordre strictement croissant).
![]() est une application injective. Donc
est une application injective. Donc ![]() est fini ou dénombrable.
est fini ou dénombrable.
![]() n’est pas fini car il contient l’ensemble infini
n’est pas fini car il contient l’ensemble infini ![]() . donc
. donc ![]() est dénombrable.
est dénombrable.
Les ensembles ![]() forment une partition de
forment une partition de ![]() et sont dénombrables, donc par réunion dénombrable d’ensembles dénombrables,
et sont dénombrables, donc par réunion dénombrable d’ensembles dénombrables, ![]() est un ensemble dénombrable.
est un ensemble dénombrable.
![]() Deuxième méthode
Deuxième méthode
On note ![]() l’ensemble des parties finies de
l’ensemble des parties finies de ![]() dont le plus grand élément est égal à
dont le plus grand élément est égal à ![]() .
.
Se donner un élément de ![]() revient à se donner une partie de
revient à se donner une partie de ![]() et à lui ajouter l’élément
et à lui ajouter l’élément ![]() .
.
Donc ![]() (car le nombre de parties de
(car le nombre de parties de ![]() est égal à
est égal à ![]() ).
).
Les ensembles ![]() forment une partition de
forment une partition de ![]() et sont finis, donc par réunion dénombrable d’ensembles finis,
et sont finis, donc par réunion dénombrable d’ensembles finis, ![]() est un ensemble dénombrable ou fini.
est un ensemble dénombrable ou fini.
![]() contient la famille infinie
contient la famille infinie ![]() , donc
, donc ![]() est dénombrable.
est dénombrable.
Question 2
On suppose que l’ensemble ![]() des parties non vides de
des parties non vides de ![]() est dénombrable.
est dénombrable.
Il existe donc une application ![]() de
de ![]() dans
dans ![]() bijective.
bijective.
Pour tout ![]() , on note
, on note ![]() .
.
On note ![]() la partie de
la partie de ![]() définie ainsi :
définie ainsi : ![]() .
.
![]() est une partie de
est une partie de ![]() . Il existe donc
. Il existe donc ![]() tel que
tel que ![]() .
.
Or si ![]() et si
et si ![]() , donc
, donc ![]() . On aboutit à une contradiction.
. On aboutit à une contradiction.
L’ensemble des parties non vides de ![]() est non dénombrable. Il en est de même de l’ensemble des parties de
est non dénombrable. Il en est de même de l’ensemble des parties de ![]() .
.
Exercice 4 :
Soit ![]() une famille d’intervalles ouverts non vides et 2 à 2 disjoints de
une famille d’intervalles ouverts non vides et 2 à 2 disjoints de ![]() .
.
![]() est au plus dénombrable ?
est au plus dénombrable ?
Corrigé de l’exercice 4 :
En utilisant la densité de ![]() , pour tout
, pour tout ![]() , il existe
, il existe ![]() .
.
Si ![]() ,
, ![]() car
car ![]() .
.
On définit ainsi une injection ![]() .
.
Comme il existe une bijection ![]() ,
, ![]() est une injection de
est une injection de ![]() dans
dans ![]() , alors
, alors ![]() est fini ou dénombrable.
est fini ou dénombrable.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
2. Exercies sur les dénombrements en maths spé
Exercice 5 :
On tire 5 cartes d’un jeu de 32 cartes. Quel est le nombre de mains contenant 2 as ?
Corrigé de l’exercice 5 :
On choisit 2 as parmi 4 de ![]() façons.
façons.
Puis on choisit 3 cartes parmi les ![]() cartes sans as de
cartes sans as de ![]() façons.
façons.
Le nombre de mains contenant deux as est égal à ![]() .
.
Exercice 6 :
Quel est le nombre de mains de 4 cartes d’un jeu de 32 cartes contenant 2 rois ou 3 dames ?
Corrigé de l’exercice 6 :
On ne peut pas avoir deux rois et trois dames en même temps dans une main de 4 cartes.
On note ![]() l’ensemble des mains contenant 2 Rois et
l’ensemble des mains contenant 2 Rois et ![]() l’ensemble des mains contenant 3 dames.
l’ensemble des mains contenant 3 dames.
![]()
![]()
car on choisit 2 rois parmi 4 de ![]() façons puis 2 cartes parmi les 28 qui restent de
façons puis 2 cartes parmi les 28 qui restent de ![]() façons.
façons.
![]()
![]()
car on choisit 3 dames parmi 4 de ![]() façons puis 1 carte parmi les 28 qui restent de
façons puis 1 carte parmi les 28 qui restent de ![]() façons.
façons.
![]() car
car ![]() .
.
Aviez-vous pensé à écrire que les deux ensembles sont disjoints ?
Exercice 7 :
Quel est le nombre de mains de 4 cartes contenant 2 rois ou 3 trèfles d’un jeu de 32 cartes ?
Corrigé de l’exercice 7 :
On peut obtenir une main contenant le roi de trèfle.
Soit ![]() l’ensemble des mains contenant
l’ensemble des mains contenant ![]() rois et
rois et ![]() l’ensemble des mains de 4 cartes contenant
l’ensemble des mains de 4 cartes contenant ![]() trèfles.
trèfles.
![]()
![]()
car on choisit ![]() rois parmi
rois parmi ![]() de
de ![]() façons puis
façons puis ![]() cartes parmi les
cartes parmi les ![]() qui restent de
qui restent de ![]() façons.
façons.
![]()
![]()
car on choisit ![]() trèfles parmi
trèfles parmi ![]() de
de ![]() façons puis
façons puis ![]() carte parmi les
carte parmi les ![]() qui restent de
qui restent de ![]() façons.
façons.
![]()
![]()
C’est l’ensemble des mains contenant le roi de trèfle, un autre roi et ![]() autres trèfles.
autres trèfles.
On choisit un roi qui n’est pas de trèfle (![]() choix), deux trèfles différents du roi de
choix), deux trèfles différents du roi de ![]() façons.
façons.
![]()
![]() .
.
Exercice 8 :
Soit ![]() un ensemble de cardinal
un ensemble de cardinal ![]() . Soit
. Soit ![]() l’ensemble des parties de
l’ensemble des parties de ![]() ayant un nombre pair d’éléments.
ayant un nombre pair d’éléments.
Déterminer ![]() .
.
Corrigé de l’exercice 8 :
On note ![]() (la partie entière de
(la partie entière de ![]() ).
).
Si ![]() , on note
, on note ![]() l’ensemble des parties de
l’ensemble des parties de ![]() à
à ![]() éléments.
éléments.
La famille ![]() forme une partition de
forme une partition de ![]() .
.
Donc 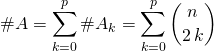
![]() (pour le calcul de la somme, voir l’exercice 3 du §2.4. dans la partie méthodes).
(pour le calcul de la somme, voir l’exercice 3 du §2.4. dans la partie méthodes).
Exercice 9
Soient ![]() et
et ![]() trois entiers naturels non nuls avec
trois entiers naturels non nuls avec ![]() .
.
En utilisant un raisonnement de dénombrement, démontrer la formule de Vandermonde :
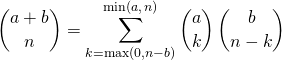 .
.
Corrigé de l’exercice 9 :
Soient ![]() et
et ![]() .
.
![]() et
et ![]() sont disjoints et ont respective- ment
sont disjoints et ont respective- ment ![]() et
et ![]() éléments.
éléments. ![]() .
.
![]() On note
On note ![]() l’ensemble des parties de
l’ensemble des parties de ![]() ayant
ayant ![]() éléments.
éléments. ![]() .
.
![]() On note
On note ![]() l’ensemble des parties de
l’ensemble des parties de ![]() formées de
formées de ![]() éléments dans
éléments dans ![]() et
et ![]() dans
dans ![]() .
.
L’ensemble ![]() est non vide
est non vide
ssi ![]() et
et ![]()
ssi ![]() .
.
Les ensembles (![]() forment une partition de
forment une partition de ![]() .
.
![]() car on doit choisir
car on doit choisir ![]() éléments parmi
éléments parmi ![]() et
et ![]() éléments parmi
éléments parmi ![]() .
.
![]()
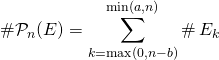
soit 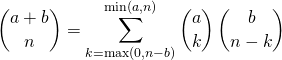 .
.
D’autres chapitres de mathématiques peuvent être révisés par les étudiants en CPGE, en se rendant sur les pages de cours en ligne de Maths en Maths Spé. Sont accessibles, les cours en ligne de Maths en PC, la page de cours en ligne de Maths en MP et la page de cours en ligne de Maths en PSI.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
2. Exercices sur les les surjections en maths spé
Exercice 10 :
Si ![]() , on note
, on note ![]() .
.
Soient ![]() et
et ![]() deux entiers naturels non nuls. On note
deux entiers naturels non nuls. On note ![]() le nombre de surjections de
le nombre de surjections de ![]() dans
dans ![]() .
.
Question 1
Donner les valeurs de ![]() et de
et de ![]() si
si ![]() .
.
Question 2
Calculer ![]() .
.
Question 3
Calculer ![]() .
.
Question 4
Calculer ![]() .
.
Question 5
Si ![]() ,
,
![]()
![]() .
.
Question 6
Montrer que 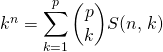
Question 7
Si ![]() ,
,
![]() est égal à
est égal à ![]()
Corrigé de l’exercice 10 :
Question 1 :
![]() Une application de
Une application de ![]() dans lui-même est une surjection ssi elle est bijective, donc
dans lui-même est une surjection ssi elle est bijective, donc ![]() .
.
![]() Il n’y a aucune surjection de
Il n’y a aucune surjection de ![]() dans
dans ![]() lorsque
lorsque ![]() car une application de
car une application de ![]() dans
dans ![]() a au plus
a au plus ![]() images distinctes.
images distinctes.
Question 2 :
Une application de ![]() dans
dans ![]() est surjective ssi elle n’est pas constante. Il y a
est surjective ssi elle n’est pas constante. Il y a ![]() applications de
applications de ![]() dans
dans ![]() et deux applications constantes, donc
et deux applications constantes, donc ![]() .
.
Question 3
On note ![]() l’ensemble des applications de
l’ensemble des applications de ![]() dans
dans ![]() .
. ![]() .
.
On forme une partition de ![]() de la façon suivante :
de la façon suivante :
![]()
![]() est l’ensemble des applications constantes : il y en a 3.
est l’ensemble des applications constantes : il y en a 3.
![]()
![]() est l’ensemble des applications dont l’image est une partie à deux éléments.
est l’ensemble des applications dont l’image est une partie à deux éléments.
Pour définir un élément de ![]() , on se donne une partie de
, on se donne une partie de ![]() à deux éléments (ce qui se fait de
à deux éléments (ce qui se fait de ![]() façons). Puis on définit une application surjective de
façons). Puis on définit une application surjective de ![]() dans cet ensemble. En utilisant la question 2, il y a
dans cet ensemble. En utilisant la question 2, il y a ![]() applications de ce type.
applications de ce type.
Donc ![]() .
.
![]()
![]() est l’ensemble des surjections.
est l’ensemble des surjections.
Comme ![]() , on en déduit que
, on en déduit que ![]() .
.
Question 4 :
Pour définir une surjection de ![]() dans
dans ![]()
![]() on choisit l’élément
on choisit l’élément ![]() de
de ![]() ayant deux antécédents : il y a
ayant deux antécédents : il y a ![]() choix pour
choix pour ![]() .
.
![]() on se donne les deux éléments
on se donne les deux éléments ![]() de
de ![]() d’image égale à
d’image égale à ![]() : il y a
: il y a ![]() choix.
choix.
![]() on définit une surjection (donc une bijection) de
on définit une surjection (donc une bijection) de ![]() dans
dans ![]() ce qui se fait de
ce qui se fait de ![]() façons.
façons.
Donc ![]()
![]() .
.
Question 5 :
On note ![]() l’ensemble des surjections de
l’ensemble des surjections de ![]() dans
dans ![]() .
.
On écrit que ![]() où
où
![]() est l’ensemble des surjections
est l’ensemble des surjections ![]() de
de ![]() dans
dans ![]() telles que la restriction de
telles que la restriction de ![]() à
à ![]() soit une surjection de
soit une surjection de ![]() sur
sur ![]() et
et ![]() est l’ensemble des surjections
est l’ensemble des surjections ![]() de
de ![]() dans
dans ![]() telles que cette restriction ne soit pas surjective .
telles que cette restriction ne soit pas surjective .
![]() Se donner un élément
Se donner un élément ![]() de
de ![]() revient à se donner une surjection
revient à se donner une surjection ![]() de
de ![]() dans
dans ![]() et à donner
et à donner ![]() quelconque dans
quelconque dans ![]() (
(![]() choix pour
choix pour ![]() ) donc
) donc ![]() .
.
![]() Pour définir un élément
Pour définir un élément ![]() de
de ![]() ,
,
![]() on définit la restriction
on définit la restriction ![]() de
de ![]() à
à ![]() , un seul élément
, un seul élément ![]() de
de ![]() n’est pas atteint par
n’est pas atteint par ![]() , on choisit cet élément (
, on choisit cet élément (![]() choix), puis on définit
choix), puis on définit ![]() qui est une surjection de
qui est une surjection de ![]() sur
sur ![]() ce qui se fait de
ce qui se fait de ![]() façons
façons
![]() puis on définit
puis on définit ![]() .
.
Donc ![]()
![]() Comme
Comme ![]() et
et ![]() sont incompatibles :
sont incompatibles :
![]()
![]() .
.
Question 6 :
Si ![]() , on note
, on note ![]() l’ensemble des applications
l’ensemble des applications ![]() de
de ![]() dans
dans ![]() telles que
telles que ![]() .
.
On forme ainsi une partition de l’ensemble ![]() , ensemble des applications de
, ensemble des applications de ![]() dans
dans ![]() .
.
Donc 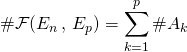 .
.
Se donner un élément ![]() de
de ![]() revient à se donner une partie
revient à se donner une partie ![]() de
de ![]() ayant
ayant ![]() éléments (de
éléments (de ![]() façons) puis à définir une application surjective de
façons) puis à définir une application surjective de ![]() dans
dans ![]() ce qui se fait de
ce qui se fait de ![]() façons.
façons.
donc ![]() .
.
On obtient donc 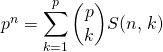 .
.
Question 7 :
Si ![]() ,
,
![]()
![]()
soit ![]() .
.
4. Exercices sur les mots de Dyck
On appelle » mot de Dyck » une chaîne de ![]() caractères,
caractères, ![]() , formée de
, formée de ![]() lettres
lettres ![]() et
et ![]() lettres
lettres ![]() , telle que, lorsque l’on dénombre les lettres de gauche à droite, en s’arrêtant à une lettre du mot, le nombre de
, telle que, lorsque l’on dénombre les lettres de gauche à droite, en s’arrêtant à une lettre du mot, le nombre de ![]() soit toujours supérieur ou égal au nombre de
soit toujours supérieur ou égal au nombre de ![]() . Ainsi, le seul mot de Dyck de longueur
. Ainsi, le seul mot de Dyck de longueur ![]() est :
est : ![]() . Les mots de Dyck de longueur 4 sont :
. Les mots de Dyck de longueur 4 sont : ![]() et
et ![]() .
.
![]() et
et ![]() sont des mots de Dyck, alors que
sont des mots de Dyck, alors que ![]() et
et ![]() n’en sont pas.
n’en sont pas.
Pour tout entier ![]() , on désigne par
, on désigne par ![]() le nombre de mots de Dyck de
le nombre de mots de Dyck de ![]() lettres.
lettres.
Question 1
Calculer ![]() .
.
Question 2
On pose : ![]() . Montrer que, pour tout entier
. Montrer que, pour tout entier 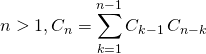
Question 3
Montrer que ![]() .
.
👍 ![]() est appelé le
est appelé le ![]() -ième nombre de Catalan.
-ième nombre de Catalan.
Question 4 : Une application
Une particule se déplace sur une droite graduée en partant de l’origine et en se déplaçant à chaque minute d’une unité vers la droite ou vers la gauche.
Le nombre de façons de revenir pour la première fois à l’instant ![]() en
en ![]() est égal à
est égal à ![]()
Si toutes les réponses à ces exercices sont correctes, il faut désormais passer aux entraînements sur les annales. Mais, si vous souhaitez vous entraîner sur d’autres exercices de cours en ligne, vous avez le choix. Quelques idées de chapitres au programme de Maths Spé :

