Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Espaces vectoriels normés en MP, PC, PSI
Résumé de cours Exercices et corrigés
Exercices et corrigés sur les espaces vectoriels normés et topologie
1. Sur les normes
Exercice 1
Soit ![]() l’ensemble des suites réelles bornées.
l’ensemble des suites réelles bornées.
On rappelle que ![]() définit une norme sur
définit une norme sur ![]() .
.
On définit ![]() .
.
Question 1
Montrer que ![]() est une norme sur
est une norme sur ![]() .
.
Question 2
Montrer que ![]() et
et ![]() sont équivalentes et donner les valeurs optimales de
sont équivalentes et donner les valeurs optimales de ![]() et
et ![]() telles que
telles que ![]() .
.
Corrigé de l’exercice 1 :
Question 1 :
On sait que ![]() est une norme sur
est une norme sur ![]() .
.
On remarquera l’utilisation de la norme ![]() et de ses propriétés qui évite les démonstrations « pénibles » sur les sup pour la norme
et de ses propriétés qui évite les démonstrations « pénibles » sur les sup pour la norme ![]() .
.
![]()
![]() est défini car l’ensemble
est défini car l’ensemble ![]() est borné et
est borné et ![]() , donc
, donc ![]() .
.
De plus, en utilisant ![]() ,
,
on en déduit que ![]() .
.
![]() Séparation.
Séparation.
Si ![]() , comme
, comme ![]() ,
, ![]() ;
; ![]() étant une norme,
étant une norme, ![]() .
.
![]() Homogénéité.
Homogénéité.
Soit ![]() et
et ![]() .
.
Soit ![]() où
où ![]() ,
,
![]() .
.
![]() Inégalité triangulaire. Soit
Inégalité triangulaire. Soit ![]() .
.
On note ![]() où pour tout
où pour tout ![]() ,
,
![]() et
et ![]() ,
,
![]() où
où ![]() .
.
![]() , alors
, alors ![]()
Donc ![]() soit
soit ![]()
On a prouvé que ![]() est une norme.
est une norme.
Question 2 :
Dans la question 1, on a montré que ![]() .
.
Soiet ![]() et
et ![]() des réels strictement positifs tels que
des réels strictement positifs tels que ![]() .
.
![]() En prenant
En prenant ![]() avec
avec ![]() et si
et si ![]() ,
, ![]() et
et ![]() , donc
, donc ![]() .
.
![]() En prenant
En prenant ![]() avec
avec ![]() et
et ![]() pour tout
pour tout ![]() .
.
![]() .
.
![]() selon que
selon que ![]() est pair ou impair.
est pair ou impair.
Donc ![]() , alors
, alors ![]() .
.
Les coefficients optimaux sont ![]() et
et ![]() .
.
Exercice 2
Soit ![]() et
et ![]() deux entiers naturels supérieurs ou égaux à 1.
deux entiers naturels supérieurs ou égaux à 1.
On introduit ![]() des réels 2 à 2 distincts. Soit
des réels 2 à 2 distincts. Soit ![]() .
.
Trouver une CNS pour que ![]() ,
, 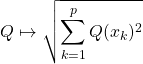 définisse une norme sur
définisse une norme sur ![]() .
.
Corrigé de l’exercice 2 :
![]() Si
Si ![]() et
et 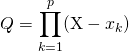 ,
, ![]() car
car ![]() et
et ![]() avec
avec ![]() ;
; ![]() n’est pas une norme sur
n’est pas une norme sur ![]() .
.
![]() On suppose que
On suppose que ![]() .
.
On démontre que ![]() est une norme euclidienne.
est une norme euclidienne.
On introduit  .
.
![]() Il est simple de prouver que pour tout
Il est simple de prouver que pour tout ![]() ,
, ![]() est linéaire.
est linéaire.
![]() Par commutativité de la multiplication des réels,
Par commutativité de la multiplication des réels, ![]() .
.
![]() Pour tout
Pour tout ![]() ,
, ![]() .
.
![]() Si
Si ![]() vérifie
vérifie ![]() , comme somme nulle de réels positifs ou nuls, pour tout
, comme somme nulle de réels positifs ou nuls, pour tout ![]() , le polynôme
, le polynôme ![]() de degré inférieur ou égal à
de degré inférieur ou égal à ![]() admet
admet ![]() racines distinctes, donc
racines distinctes, donc ![]() .
.
On a prouvé que ![]() est un produit scalaire et donc
est un produit scalaire et donc ![]() est une norme euclidienne.
est une norme euclidienne.
Exercice 3
Soit ![]() une norme sur
une norme sur ![]() .
.
Montrer qu’il existe une constante ![]() telle que
telle que ![]() .
.
Corrigé de l’exercice 3 :
L’application ![]() ,
, ![]() est bilinéaire donc continue puisque
est bilinéaire donc continue puisque ![]() est de dimension finie.
est de dimension finie.
L’application ![]() est continue par composée de fonctions continues.
est continue par composée de fonctions continues.
![]() est un compact de
est un compact de ![]() , donc
, donc ![]() est un compact de
est un compact de ![]() .
.
La fonction ![]() est bornée sur ce compact, il existe donc
est bornée sur ce compact, il existe donc ![]() tel que si
tel que si ![]() ,
, ![]() .
.
Soient ![]() et
et ![]() deux éléments non nuls de
deux éléments non nuls de ![]() , on note
, on note ![]() et
et ![]() .
.
![]() et
et ![]() ont une norme égale à 1, l’inégalité
ont une norme égale à 1, l’inégalité ![]() s’écrit aussi par homogénéité de la norme :
s’écrit aussi par homogénéité de la norme : ![]() .
.
Cette inégalité reste vraie si ![]() ou
ou ![]() est la matrice nulle.
est la matrice nulle.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
2. Limites de matrices
Exercice 4
Soit ![]() vérifiant la relation
vérifiant la relation ![]() .
.
Montrer que la suite ![]() converge vers une matrice de projection.
converge vers une matrice de projection.
Corrigé de l’exercice 4 :
Soit
Il existe une matrice
Alors
Comme
On note
Par continuité de l’endomorphisme de
L’application bilinéaire définie par
⚠️ Il n’y a aucun théorème sur les limites de produit de suites de vecteurs, ces produits n’étant pas définis en général.
👍 Il faudra systématiquement faire la démonstration pour des limites de produits de matrices, en général en utilisant la continuité d’applications linéaires de la forme ![]() ou
ou ![]() ou d’applications bilinéaires de la forme
ou d’applications bilinéaires de la forme ![]() .
.
Exercice 5
Soit si ![]() ,
, ![]() .
.
Question 1
Déterminer un réel ![]() et un réel
et un réel ![]() tel que
tel que ![]() où
où
![]() .
.
Question 2
En déduire la limite de la suite ![]() .
.
Corrigé de l’exercice 5 :
Question 1 :
On cherche un réel ![]() et un réel
et un réel ![]() tels que
tels que ![]() et
et ![]() .
.
Il suffit de choisir ![]() et
et ![]() .
.
Car alors ![]() , donc
, donc ![]() car
car ![]() et
et ![]() .
.
Question 2 :
En utilisant ![]() , (propriétés des matrices de rotation vues en MPSI)
, (propriétés des matrices de rotation vues en MPSI)
![]() .
.
![]()
![]() , donc
, donc ![]() alors
alors ![]()
![]() , donc
, donc ![]() .
.
Alors ![]() .
.
On rappelle que pour déterminer la limite d’une suite de matrices, il suffit de chercher les limites de chacune des suites coordonnées.
3. Continuité des applications linéaires
Exercice 6
Soit ![]() .
.
Il existe ![]() tel que pour tout
tel que pour tout ![]() ,
, 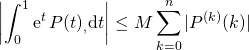 .
.
Corrigé de l’exercice 6 :
a) On démontre que 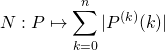 définit une norme sur
définit une norme sur ![]() .
.
![]()
![]() est bien définie et à valeurs positives ou nulles.
est bien définie et à valeurs positives ou nulles.
![]() On suppose que
On suppose que ![]() , alors pour tout
, alors pour tout ![]() comme somme nulle de réels positifs ou nuls.
comme somme nulle de réels positifs ou nuls.
Si ![]() était non nul, on pourrait noter
était non nul, on pourrait noter ![]() son degré et
son degré et ![]() son coefficient dominant, alors
son coefficient dominant, alors ![]() , on aboutit donc à une contradiction.
, on aboutit donc à une contradiction.
On en déduit que ![]() .
.
![]() L’homogénéité résulte de la sommation des relations
L’homogénéité résulte de la sommation des relations ![]()
![]() Si
Si ![]() , pour tout
, pour tout ![]() ,
, ![]() , et par sommation, on obtient l’inégalité triangulaire
, et par sommation, on obtient l’inégalité triangulaire ![]() .
.
b) L’application ![]() est linéaire et
est linéaire et ![]() est de dimension finie, elle est lipschitzienne, donc il existe
est de dimension finie, elle est lipschitzienne, donc il existe ![]() tel que
tel que ![]() , de plus
, de plus ![]() car
car ![]() .
.
On a donc justifié l’inégalité demandée.
Exercice 7
Soient ![]() et
et ![]() deux espaces vectoriels normés et
deux espaces vectoriels normés et ![]() une application de
une application de ![]() dans
dans ![]() telle que :
telle que :
![]()
![]()
![]()
![]() tel que
tel que
![]()
![]()
![]() .
.
Question 1
Montrer que ![]() est lipschitzienne.
est lipschitzienne.
Question 2
En déduire que ![]() est linéaire.
est linéaire.
Corrigé de l’exercice 7 :
Question 1 :
![]() En prenant
En prenant ![]() , on obtient
, on obtient ![]() , donc
, donc ![]() .
.
![]() En prenant
En prenant ![]() où
où ![]() ,
, ![]() donc
donc ![]() .
.
![]() Soit
Soit ![]() et
et ![]() , on note
, on note ![]() , donc
, donc ![]() ,
,
![]() soit
soit ![]() donc
donc ![]() .(*)
.(*)
L’inégalité reste vraie si ![]() .
.
Puis si ![]() sont dans
sont dans ![]() ,
, ![]()
![]() .
.
En utilisant l’inégalité (*) en ![]() :
:
![]() .
.
![]() est
est ![]() -lipschitzienne.
-lipschitzienne.
Question 2 :
![]() Par récurrence, on démontre que
Par récurrence, on démontre que ![]() .
.
![]() Comme
Comme ![]() est impaire, pour tout
est impaire, pour tout ![]() et
et ![]() ,
, ![]() .
.
![]() Soit
Soit ![]() , on note
, on note ![]() avec
avec ![]() et
et ![]() , soit
, soit ![]() ,
, ![]() .
.
![]() donc
donc ![]() soit
soit ![]() .
.
![]() Soit
Soit ![]() , il existe une suite
, il existe une suite ![]() de rationnels qui converge vers
de rationnels qui converge vers ![]() , pour tout
, pour tout ![]() ,
, ![]() .
.
Comme ![]() est continue, par caractérisation séquentielle de la continuité, on obtient :
est continue, par caractérisation séquentielle de la continuité, on obtient : ![]()
On a donc prouvé que ![]() est linéaire.
est linéaire.
Exercice 8
Soit ![]() muni de la norme de la convergence en moyenne.
muni de la norme de la convergence en moyenne.
Soit ![]() ,
, ![]() où
où ![]() est la primitive de
est la primitive de ![]() nulle en
nulle en ![]() .
.
Question 1
![]() est continue de
est continue de ![]() dans
dans ![]() ?
?
Question 2
Déterminer : ![]() .
.
Corrigé de l’exercice 8 :
Question 1 :
Pour tout ![]() ,
, ![]() , donc
, donc ![]()
puis par intégration, ![]() soit
soit ![]() ou
ou ![]() , alors si
, alors si ![]() ,
, ![]() ce qui prouve la continuité de l’application linéaire
ce qui prouve la continuité de l’application linéaire ![]() .
.
![]() On vient de montrer que 1 est un majorant de
On vient de montrer que 1 est un majorant de ![]() donc
donc ![]() .
.
![]()
![]() est continue et positive, donc
est continue et positive, donc ![]()
![]() .
.
![]() est définie pour
est définie pour ![]() par
par ![]()
![]()
![]()
Comme ![]() , en passant à la limite, on obtient
, en passant à la limite, on obtient ![]() .
.
Par double inégalité, ![]() .
.
Des révisions régulières sont essentielles pour réussir en Maths Spé, et bien sûr réussir les concours post-prépa. Les cours en ligne de Maths en MP, les cours en ligne de Maths en PC et les cours en ligne de PSI en Maths sont réalisés spécialement pour aider et accompagner les étudiants dans leur réussite.
4. Ouverts et fermés
Exercice 9
Soit ![]() et
et ![]() l’ensemble des
l’ensemble des ![]() tels que
tels que ![]() prend au moins une fois une valeur strictement négative.
prend au moins une fois une valeur strictement négative.
Montrer que ![]() est un ouvert de
est un ouvert de ![]() .
.
Corrigé de l’exercice 9 :
On remarque que ![]() .
.
Si ![]() est fixé dans
est fixé dans ![]() , l’application
, l’application ![]() ,
, ![]() est une forme linéaire définie sur un espace vectoriel de dimension finie, elle est donc continue.
est une forme linéaire définie sur un espace vectoriel de dimension finie, elle est donc continue.
![]() est un ouvert comme image réciproque de l’ouvert
est un ouvert comme image réciproque de l’ouvert ![]() par
par ![]() .
.
![]() est un ouvert comme réunion d’ouverts.
est un ouvert comme réunion d’ouverts.
Exercice 10
Soit ![]() une suite de réels strictement croissante.
une suite de réels strictement croissante.
On note ![]() .
.
Montrer que ![]() est un fermé de
est un fermé de ![]() ssi
ssi ![]() .
.
Corrigé de l’exercice 10 :
![]() Si la suite
Si la suite ![]() converge vers
converge vers ![]() , comme la suite est strictement croissante, pour tout
, comme la suite est strictement croissante, pour tout ![]() . Le vecteur
. Le vecteur ![]() est adhérent à
est adhérent à ![]() , car la suite
, car la suite ![]() est une suite de
est une suite de ![]() qui converge vers
qui converge vers ![]() et
et ![]() , donc
, donc ![]() n’est pas fermé.
n’est pas fermé.
![]() On suppose que
On suppose que ![]() ,
, ![Rendered by QuickLaTeX.com \displaystyle \textrm{C} _{\mathbb{R}} E\, =\, ] - \infty , \, u_0[ \; \cup\; \left ( \bigcup_{n = 0}^ {+\infty}\; ] u_n , \, u_{n + 1}[ \right )](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-efb31d81eb0a79f6c9a5026d28264cce_l3.png) est une réunion d’ouverts, donc est un ouvert, alors
est une réunion d’ouverts, donc est un ouvert, alors ![]() est un fermé.
est un fermé.
Exercice 11
Soit ![]() un evn.
un evn.
Question 1
Si ![]() est un ouvert non vide et
est un ouvert non vide et ![]() une partie non vide de
une partie non vide de ![]() ,
,
![]() est un ouvert de
est un ouvert de ![]() .
.
Question 2
Soit ![]() un fermé et
un fermé et ![]() un compact. Montrer que
un compact. Montrer que ![]() est fermé.
est fermé.
Question 3
Soit ![]() et
et ![]() .
.
![]() et
et ![]() sont deux fermés de
sont deux fermés de ![]() tels que
tels que ![]() n’est pas fermé ?
n’est pas fermé ?
Question 4
Soit ![]() un compact de
un compact de ![]() tel que
tel que ![]() .
.
Montrer que ![]() est fermé.
est fermé.
Corrigé de l’exercice 11 :
Question 1
Soit ![]() , comme
, comme ![]() est un ouvert contenant
est un ouvert contenant ![]() , il existe
, il existe ![]() tel que
tel que ![]() .
.
Pour tout ![]() , alors
, alors ![]() donc
donc ![]() et on a écrit
et on a écrit
![]() avec
avec ![]() et
et ![]() ce qui prouve que
ce qui prouve que ![]() .
.
On a donc montré que ![]() .
.
![]() est un ouvert de
est un ouvert de ![]() .
.
Question 2 :
On introduit une suite ![]() de
de ![]() qui converge vers
qui converge vers ![]() dans
dans ![]() . On écrit pour tout
. On écrit pour tout ![]() ,
, ![]() avec
avec ![]() et
et ![]() .
.
![]() est une suite du compact
est une suite du compact ![]() , il existe une suite extraite
, il existe une suite extraite ![]() qui converge vers
qui converge vers ![]() .
.
Alors ![]() et
et ![]() .
.
Comme ![]() est un fermé,
est un fermé, ![]() , donc
, donc ![]() avec
avec ![]() et
et ![]() , alors
, alors ![]() est un fermé par caractérisation séquentielle des fermés.
est un fermé par caractérisation séquentielle des fermés.
Question 3 :
![Rendered by QuickLaTeX.com \displaystyle \textrm{C} \, K \; =\; ]- \infty ,\, 1[\, \cup \, \bigcup_{n = 1}^{+\infty}\; ]n ,\, n + 1[](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-f0c414ade704269f909dd896093cc518_l3.png) est une réunion d’ouverts, donc est un ouvert.
est une réunion d’ouverts, donc est un ouvert.Alors
On démontre que
![Rendered by QuickLaTeX.com \displaystyle \textrm{C} \, A= \left( \bigcup_{n = 1}^{+\infty}\; ]u_{n +1},\, u_{ n}[ \right ) \; \cup \; ] u_0 , \, + \infty[](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-ab21464c6cf6268abeb63d4ef3be8ee0_l3.png) puisque pour tout
puisque pour tout On applique ce résultat à la suite définie pour
il suffit de remarquer que
Donc
On démontre que
Si
Donc
Question 4 :
Soit pour tout ![]() ,
, ![]() où
où ![]() et
et ![]() .
.
On suppose que ![]() .
.
![]() est une suite du compact
est une suite du compact ![]() , il existe une suite extraite
, il existe une suite extraite ![]() qui converge vers
qui converge vers ![]() ,
, ![]() car
car ![]() .
.
![]() et
et ![]() donc
donc ![]() .
.
La suite ![]() est une suite de réels bornée, elle admet une suite extraite
est une suite de réels bornée, elle admet une suite extraite ![]() qui converge vers
qui converge vers ![]() .
.
Alors ![]()
donne ![]() , comme
, comme ![]() ,
, ![]() , donc
, donc ![]() .
.
On a établi que ![]() est un fermé.
est un fermé.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
5. Continuité et topologie.
Exercice 12
Soient ![]() et
et ![]() deux espaces vectoriels normés et
deux espaces vectoriels normés et ![]() une application de
une application de ![]() dans
dans ![]() .
.
![]() est continue de
est continue de ![]() dans
dans ![]()
![]() pour tout
pour tout ![]() ,
, ![]() .
.
Corrigé de l’exercice 12 :
![]() On suppose que
On suppose que ![]() est continue de
est continue de ![]() dans
dans ![]() .
.
Soit ![]() une partie non vide de
une partie non vide de ![]() (sinon l’inclusion est évidente).
(sinon l’inclusion est évidente).
Si ![]() il existe
il existe ![]() tel que
tel que ![]() .
.
Soit ![]() une suite de
une suite de ![]() telle que
telle que ![]()
Par continuité de ![]() ,
, ![]() , donc
, donc ![]() est la limite de la suite
est la limite de la suite ![]() de points de
de points de ![]() et
et ![]() .
.
On a prouvé que pour tout ![]() ,
, ![]() .
.
![]() On suppose que pour tout
On suppose que pour tout ![]() ,
, ![]() .
.
Soit ![]() . Soit
. Soit ![]() une suite de
une suite de ![]() qui converge vers
qui converge vers ![]() .
.
On raisonne par l’absurde et on suppose que la suite ![]() ne converge pas vers
ne converge pas vers ![]() .
.
Il existe donc ![]() tel que pour tout
tel que pour tout ![]() , il existe
, il existe ![]() tel que
tel que ![]() ; on construit ainsi une suite extraite
; on construit ainsi une suite extraite ![]() telle que
telle que ![]() .
.
On note ![]() ,
, ![]() est un point adhérent à
est un point adhérent à ![]() .
.
![]() implique
implique ![]() .
.
Comme ![]() , pour le réel
, pour le réel ![]() ,
, ![]() rencontre
rencontre ![]() ce qui contredit la construction de la suite
ce qui contredit la construction de la suite ![]() .
.
On en déduit que la suite ![]() converge vers
converge vers ![]() .
.
![]() est donc continue en
est donc continue en ![]() .
.
Exercice 13
Soit ![]() un espace vectoriel normé.
un espace vectoriel normé.
Question 1
Soient ![]() et
et ![]() deux parties compactes non vides de
deux parties compactes non vides de ![]() .
.
Montrer qu’il existe ![]() et
et ![]() tels que
tels que ![]() .
.
Question 2
On suppose que ![]() est un espace vectoriel de dimension finie.
est un espace vectoriel de dimension finie.
Montrer que le résultat précédent est valable si l’on suppose seulement ![]() compact et
compact et ![]() fermé non vides.
fermé non vides.
Corrigé de l’exercice 13 :
Question 1 :
On considère l’application ![]()
On utilise la norme ![]() sur
sur ![]() définie par :
définie par : ![]() ;
; ![]() est une application linéaire de
est une application linéaire de ![]() dans
dans ![]() vérifiant :
vérifiant : ![]() ,
, ![]() .
.
En utilisant la linéarité de![]() , on en déduit que
, on en déduit que ![]() est lipschitizienne donc continue.
est lipschitizienne donc continue.
On en déduit que ![]() est continue.
est continue.
![]() est une partie compacte de
est une partie compacte de ![]() , donc
, donc ![]() admet un minimum sur
admet un minimum sur ![]() , il existe donc
, il existe donc ![]() tel que
tel que ![]() .
.
Question 2 :
La suite
Soit
Pour tout
La suite
On note
La suite

