Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Intégrales à paramètre en MP, PC, PSI, PT
Résumé de cours Exercices et corrigés
Exercices et corrigés – Intégrales à paramètre
1. Calcul de l’intégrale de Dirichlet
Mines-Ponts PSI 2018
Soit ![]() .
.
Question 1
Montrer que ![]() est continue sur
est continue sur ![]() .
.
Question 2
Montrer que ![]() est de classe
est de classe ![]() sur
sur ![]()
Question 3
Trouver les limites de ![]() et
et ![]() en
en ![]() .
.
Question 4
Déterminer ![]() pour
pour ![]() .
.
Question 5
En déduire la valeur de ![]() .
.
Corrigé de l’exercice :
Question 1 :
Deux résultats utiles dans la suite :
![]() Soit
Soit ![]() .
.
En utilisant ![]() , on prolonge
, on prolonge ![]() par continuité en
par continuité en ![]() en posant
en posant ![]() .
.
Puis en utilisant si ![]() ,
, ![]() , par domination,
, par domination, ![]() est intégrable sur
est intégrable sur ![]() donc
donc ![]() est intégrable sur
est intégrable sur ![]() .
.
![]() On utilisant
On utilisant ![]() , on obtient
, on obtient ![]() .
.
Continuité de ![]() .
.
On note ![]() .
.
![]() Pour tout
Pour tout ![]() ,
, ![]() est continue sur
est continue sur ![]() .
.
![]() Pour tout
Pour tout ![]() et on a prouvé que
et on a prouvé que ![]() est continue et intégrable sur
est continue et intégrable sur ![]() .
.
Par le théorème de continuité des intégrales à paramètre, la fonction ![]() est définie et continue sur
est définie et continue sur ![]() .
.
Question 2 :
On rappelle que l’on a prouvé que ![]() . (*)
. (*)
![]() Pour tout
Pour tout ![]() ,
, ![]() est continue et intégrable sur
est continue et intégrable sur ![]() .
.
![]() Pour tout
Pour tout ![]() ,
, ![]() est de classe
est de classe ![]() sur
sur ![]() .
.
![]()
![]()
![]()
![]()
![]() Soit
Soit ![]() , si
, si ![]() ,
,
![]()
![]() (par (*))
(par (*))
![]()
![]()
Les fonctions ![]() et
et ![]() sont continues et intégrables sur
sont continues et intégrables sur ![]() (il n’y a pas de problème pour
(il n’y a pas de problème pour ![]() ; pour
; pour ![]() , on utilise
, on utilise ![]() ).
).
![]()
![]() Par le théorème de dérivation des intégrales à paramètre, la fonction
Par le théorème de dérivation des intégrales à paramètre, la fonction ![]() est de classe
est de classe ![]() sur
sur ![]() et
et
![]()
![]() .
.
![]() .
.
![]()
![]() .
.
![]() .
.
COURS PARTICULIERS EN CPGE MATHS SPE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers pour les élèves de Maths Spé
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Question 3 :
En utilisant ![]() , pour tout
, pour tout ![]() ,
,
![]() , donc par encadrement,
, donc par encadrement, ![]() .
.
De même, ![]() .
.
On démontre facilement que ![]()
![]() .
.
Donc par encadrement, ![]() .
.
Question 4 :
![]() On commence par calculer
On commence par calculer ![]() .
.
On calcule ![]()
![]() .
.
![]() .
.
![]() .
.
![]() .
.
Donc ![]() .
.
![]() Calcul de
Calcul de ![]() .
.
On en déduit qu’il existe ![]() pour tout
pour tout ![]()
![]()
![]()
En passant à la limite, on obtient ![]() .
.
![]() Calcul de
Calcul de ![]() .
.
On cherche une primitive ![]() de
de ![]() en intégrant par parties :
en intégrant par parties :
![]()
![]()
et comme ![]() ,
,
![]()
![]()
![]()
Il existe un réel ![]() tel que pour tout
tel que pour tout ![]()
![]()
![]()
Comme ![]() ,
, ![]()
En passant à la limite (![]() ) , on obtient
) , on obtient ![]() .
.
Alors pour tout ![]() ,
, ![]()
![]() .
.
Question 5 :
Comme ![]() est continue en
est continue en ![]() ,
, ![]() .
.
c’est à dire ![]()
Puis les fonctions ![]() et
et ![]() sont de classe
sont de classe ![]() sur
sur ![]() ,
, ![]() est intégrable sur
est intégrable sur ![]() ,
, ![]() admet
admet ![]() pour limite en
pour limite en ![]() et en
et en ![]() , par le théorème d’intégration par parties,
, par le théorème d’intégration par parties,
![]()
On a donc prouvé que ![]() .
.
Pour accéder aux meilleurs cours particuliers à domicile ou en ligne, sélectionner le prof qu'il vous faut

2. Valeur d’une intégrale à paramètre par utilisation d’une équation différentielle
On pose ![]() .
.
Question 1
Montrer que ![]() est de classe
est de classe ![]() sur
sur ![]() .
.
Question 2
À l’aide d’une équation différentielle vérifiée par ![]() , calculer sa valeur.
, calculer sa valeur.
Corrigé de l’exercice
Question 1 :
![]() Résultat préliminaire.
Résultat préliminaire.
La fonction ![]() est continue sur
est continue sur ![]() .
.
![]()
![]() , donc
, donc ![]() est intégrable sur
est intégrable sur ![]() .
.
![]() Si
Si ![]() , donc
, donc ![]() est intégrable sur
est intégrable sur ![]() .
.
Alors ![]() est intégrable sur
est intégrable sur ![]() .
.
![]() Domaine de définition de
Domaine de définition de ![]() .
.
Soit ![]() . La fonction
. La fonction ![]() est continue sur
est continue sur ![]() et
et ![]() , donc
, donc ![]() est intégrable sur
est intégrable sur ![]() , ce qui justifie l’existence de
, ce qui justifie l’existence de ![]() sur
sur ![]() .
.
![]() On démontre que
On démontre que ![]() est de classe
est de classe ![]() sur
sur ![]() .
.
Soit ![]() .
.
On note ![]() .
.
![]() Pour tout réel
Pour tout réel ![]() ,
, ![]() est continue et intégrable sur
est continue et intégrable sur ![]() .
.
![]() Pour tout
Pour tout ![]() ,
, ![]() est de classe
est de classe ![]() sur
sur ![]() et
et ![]()
![]() Pour tout
Pour tout ![]() est continue sur
est continue sur ![]() .
.
![]() On note
On note ![]() .
.
![]()
![]() .
.
![]() est continue sur
est continue sur ![]() et vérifie
et vérifie ![]() , donc
, donc ![]() est intégrable sur
est intégrable sur ![]() .
.
Par le théorème de dérivation des intégrales à paramètres, ![]() est de classe
est de classe ![]() sur
sur ![]() et
et ![]()
Question 2 :
![]() Recherche de l’équation différentielle.
Recherche de l’équation différentielle.
On note ![]() et
et ![]()
![]() et
et ![]() sont de classe
sont de classe ![]() sur
sur ![]() ,
, ![]() est intégrable sur
est intégrable sur ![]() ,
, ![]() admet 0 pour limite en 0 et en
admet 0 pour limite en 0 et en ![]() , donc par le théorème d’intégration par parties,
, donc par le théorème d’intégration par parties,
![]() .
.
![]() .
.
![]() Résolution de l’équation différentielle.
Résolution de l’équation différentielle.
![]() admet comme primitive
admet comme primitive ![]() .
.
On en déduit qu’il existe ![]() ,
, ![]() .
.
![]() Calcul de
Calcul de ![]() .
.
La fonction ![]() est une bijection de classe
est une bijection de classe ![]() strictement croissante, par le théorème de changement de variable,
strictement croissante, par le théorème de changement de variable,
![]() .
.
En utilisant l’intégrale de Gauss, ![]() .
.
On en déduit que ![]() .
.
STAGE INTENSIF EN MATHS SPÉ
Profite de tes vacances pour gagner des points aux concours.
100% obtiennent une école d’ingénieur
58% admissibles Mines-Centrales
99% de recommandation à leurs amis
Avis Google France ★★★★★ 4,9 sur 5
3. Étude d’une intégrale à paramètre
![]() .
.
Question 1.
Trouver le domaine de définition ![]() de
de ![]() .
.
Question 2
Démontrer que ![]() est de classe
est de classe ![]() sur
sur ![]() et que
et que ![]() est strictement monotone. Trouver une équation différentielle vérifiée par
est strictement monotone. Trouver une équation différentielle vérifiée par ![]() .
.
Question 3
Etudier les limites et les branches infinies du graphe de ![]() . Tracer le graphe de
. Tracer le graphe de ![]() .
.
Corrigé de l’exercice :
Question 1:
La fonction ![]() est continue sur
est continue sur ![]() , donc pour tout
, donc pour tout ![]() ,
, ![]() est continue sur
est continue sur ![]() donc
donc ![]() est définie sur
est définie sur ![]() .
.
Question 2 :
![]()
![]() est de classe
est de classe ![]() .
.
![]() Pour tout
Pour tout ![]() ,
, ![]() est continue et intégrable sur
est continue et intégrable sur ![]() .
.
![]() Pour tout
Pour tout ![]() ,
, ![]() est de classe
est de classe ![]() sur
sur ![]() et
et ![]()
![]() Pour tout
Pour tout ![]() ,
, ![]() est continue sur
est continue sur ![]() .
.
![]() Soit
Soit ![]() , si
, si ![]() ,
, ![]() où
où ![]() .
.
La fonction ![]() est continue et intégrable sur
est continue et intégrable sur ![]() .
.
![]()
![]() La fonction
La fonction ![]() est de classe
est de classe ![]() sur
sur ![]() et
et ![]() .
.
![]() Stricte monotonie de
Stricte monotonie de ![]() .
.
Comme ![]() est continue sur
est continue sur ![]() , à valeurs négatives ou nulles et différente de la fonction nulle,
, à valeurs négatives ou nulles et différente de la fonction nulle, ![]() .
.
![]() est strictement décroissante sur
est strictement décroissante sur ![]() .
.
![]() Équation différentielle.
Équation différentielle.
![]() si
si ![]() et
et ![]() .
.
Question 3 :
![]() Limite en
Limite en ![]() .
.
Si ![]() ,
, ![]() , donc
, donc ![]() , donc par minoration
, donc par minoration ![]() .
.
Puis par division par ![]() ,
, ![]()
![]() .
.
Le graphe de ![]() admet une branche parabolique de direction Oy.
admet une branche parabolique de direction Oy.
![]() Limite en
Limite en ![]()
Si ![]() . Par encadrement,
. Par encadrement, ![]() .
.
Le graphe admet une asymptote d’équation ![]() en
en ![]() .
.
Pour accéder aux meilleurs cours particuliers à domicile ou en ligne, sélectionner le prof qu'il vous faut

Avant de s’entraîner en conditions réelles de concours, il est important pour les étudiants de Maths Spé, de s’assurer d’être à jour dans les cours et de ne souffrir d’aucune difficulté. Une petite relecture des cours en ligne de Maths en PC, des cours en ligne de Maths en PSI ou des cours en ligne de Maths en MP est fortement recommandée.
4. Généralisation de la formule de Stirling
Question 1 : deux inégalités.
a) Montrer que pour tout ![]()
![]() .
.
b) Soit ![]() , pour tout
, pour tout ![]() , montrer que
, montrer que
![]() .
.
Question 2 : convergence d’une intégrale.
On note si ![]() et
et ![]() ,
, ![]() .
.
Justifier l’existence de ![]() .
.
Question 3 : limite de l’intégrale de la question 2.
Déterminer ![]() .
.
Question 4 : Équivalent de ![]() en
en ![]() .
.
En justifiant soigneusement le changement de variable ![]() , trouver un équivalent de
, trouver un équivalent de ![]() en
en ![]() .
.
On utilisera ![]() .
.
Corrigé de l’exercice :
Question 1 :
a) On note si ![]()
![]() .
.
![]() .
.
![]() est décroissante sur
est décroissante sur ![]() et
et ![]() donc pour tout
donc pour tout ![]()
![]() .
.
b) On note si ![]()
![]()
![]()
![]()
![]()
![]()
![]() est croissante sur
est croissante sur ![]() et
et ![]() , donc pour tout
, donc pour tout ![]() , ce que l’on voulait démontrer.
, ce que l’on voulait démontrer.
Question 2 :
Soit ![]() fixé ;
fixé ; ![]() est continue sur
est continue sur ![]() .
.
Comme ![]() car
car ![]() , on prolonge
, on prolonge ![]() par continuité en
par continuité en ![]() en posant
en posant ![]() .
.
Puis ![]()
En utilisant ![]() , on obtient
, on obtient ![]() , ce qui donne
, ce qui donne ![]() , donc
, donc ![]() est intégrable sur
est intégrable sur ![]() par domination par une fonction intégrable.
par domination par une fonction intégrable.
Question 3 :
On note ![]() , où
, où ![]() si
si ![]() et
et ![]() si
si ![]() .
.
![]() Pour tout
Pour tout ![]() ,
, ![]() est continue sur
est continue sur ![]() .
.
![]() Pour tout
Pour tout ![]() , pour
, pour ![]() assez grand,
assez grand, ![]() et
et ![]() .
.
![]()
![]()
![]()
![]()
donc ![]() .
.
La fonction ![]() est continue sur
est continue sur ![]() .
.
![]() Domination : en utilisant l’inégalité
Domination : en utilisant l’inégalité ![]()
lorsque ![]() ,
, ![]()
par multiplication par ![]() et croissance de l’exponentielle, on obtient
et croissance de l’exponentielle, on obtient ![]() .
.
En utilisant pour tout ![]() ,
, ![]() ,
,
et par croissance de l’exponentielle, on obtient ![]() soit
soit ![]() .
.
On note ![]() si
si ![]() et
et ![]() si
si ![]() .
.
On a montré que si ![]()
ce qui reste vrai si ![]() .
.
La fonction ![]() est continue par morceaux sur
est continue par morceaux sur ![]() , elle est intégrable sur
, elle est intégrable sur ![]() et sur
et sur ![]() car c’est un
car c’est un ![]() au voisinage de
au voisinage de ![]() .
.
On peut donc appliquer la généralisation du théorème de convergence dominée
![]() .
.
Question 4 :
La fonction ![]()
![]() définit une bijection strictement croissante de classe
définit une bijection strictement croissante de classe ![]() , le théorème de changement de variable dans
, le théorème de changement de variable dans ![]() donne :
donne :
![]()
![]()
![]() .
.
En utilisant ![]()
on a prouvé que ![]()
soit ![]() .
.
On rappelle que si ![]() , on retrouve donc la formule de Stirling.
, on retrouve donc la formule de Stirling.
Pour accéder aux meilleurs cours particuliers à domicile ou en ligne, sélectionner le prof qu'il vous faut

5. Une expression de 
On rappelle que l’on a prouvé que ![]() .
.
Question 1
Soit ![]() . Montrer que l’intégrale
. Montrer que l’intégrale ![]() est convergente et la calculer.
est convergente et la calculer.
Question 2
Déterminer ![]() .
.
Question 3 : Calcul de ![]() .
.
En utilisant ![]() , montrer que
, montrer que ![]() .
.
Corrigé de l’exercice :
Question 1 :
![]() Convergence de l’intégrale.
Convergence de l’intégrale.
La fonction ![]() est continue sur
est continue sur ![]() et équivalente en
et équivalente en ![]() à
à ![]() qui est intégrable sur
qui est intégrable sur ![]() , donc
, donc ![]() est intégrable sur
est intégrable sur ![]() .
.
![]() Calcul par intégration par parties.
Calcul par intégration par parties.
Les fonctions ![]() et
et ![]() sont de classe
sont de classe ![]() sur
sur ![]() et vérifient
et vérifient ![]() car
car ![]()
et ![]() .
.
La fonction ![]() est intégrable sur
est intégrable sur ![]() .
.
Par le théorème d’intégration par parties,
![]() .
.
Si ![]() ,
, ![]()
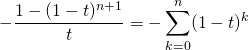
donc ![Rendered by QuickLaTeX.com \displaystyle I_n = \left [ \sum _{k = 0} ^{n } \frac {(1 - t) ^{k + 1} } {(k + 1)(n+1)} \right ] _ 0 ^1](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-036f73df9293f59ed55569072b82d41d_l3.png)
 .
.
![]()
![]() On a démontré que
On a démontré que ![]() où
où 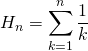 .
.
Question 2 :
On définit ![]() si
si ![]() et
et ![]() si
si ![]() .
.
Pour tout ![]() , il existe
, il existe ![]() tel que si
tel que si ![]() donc
donc ![]() , où
, où ![]() est continue sur
est continue sur ![]()
En utilisant si ![]() (il suffit d’étudier la fonction) alors si
(il suffit d’étudier la fonction) alors si ![]() ,
, ![]() puis
puis ![]() donc
donc ![]() où
où ![]()
![]() est continue sur
est continue sur ![]() et vérifie
et vérifie ![]() ,
, ![]() est intégrable par domination sur
est intégrable par domination sur ![]() .
.
Comme ![]() ,
, ![]() est intégrable sur
est intégrable sur ![]() .
.
Par le théorème de convergence dominée, ![]()
Question 3 :
La fonction ![]() est une bijection de classe
est une bijection de classe ![]() strictement croissante, par changement de variable dans l’intégrale
strictement croissante, par changement de variable dans l’intégrale ![]()
![]() , on obtient
, on obtient ![]()
![]()
![]()
![]() .
.
En utilisant ![]() , on obtient
, on obtient ![]() soit
soit ![]() donc
donc ![]() .
.
6. La fonction Béta.
On désigne par ![]() et
et ![]() deux réels strictement positifs et l’on considère l’intégrale
deux réels strictement positifs et l’on considère l’intégrale ![]() définie par
définie par
![]() .
.
Question 1.
Justifier l’existence de ![]() .
.
Question 2
![]() et
et ![]() sont égales pour tout
sont égales pour tout ![]() et
et ![]() ?
?
Question 3
Montrer que si ![]() ,
, ![]() ,
, ![]() .
.
Question 4.
Montrer que la fonction ![]() est de classe
est de classe ![]() sur
sur ![]() .
.
Corrigé de l’exercice :
Question 1 :
![]() La fonction
La fonction ![]() est continue sur
est continue sur ![]() à valeurs positives.
à valeurs positives.
![]()
![]() , donc
, donc ![]() est intégrable sur
est intégrable sur ![]() .
.
![]()
![]() , donc
, donc ![]() est intégrable sur
est intégrable sur ![]() ssi
ssi ![]() ssi
ssi ![]() .
.
On a donc justifié l’existence de ![]() pour tout
pour tout ![]() et
et ![]() .
.
Question 2 :
La fonction ![]() est une bijection de classe
est une bijection de classe ![]() et la fonction
et la fonction ![]() est intégrable sur
est intégrable sur ![]() .
.
Par le théorème de changement de variable,
![]() .
.
Question 3 :
Soient ![]() et
et ![]() .
.
![]() et
et ![]() sont de classe
sont de classe ![]() sur
sur ![]() ,
, ![]() est intégrable sur
est intégrable sur ![]() ,
, ![]() admet
admet ![]() pour limite en
pour limite en ![]() et en
et en ![]() . Par le théorème d’intégration par parties,
. Par le théorème d’intégration par parties,
![]() .
.
Puis comme ![]() ,
,
les intégrales introduites ensuite étant convergentes,
![]()
![]() .
.
soit ![]() ce qui démontre que
ce qui démontre que
![]()
soit la relation demandée.
Question 4 :
On fixe ![]() .
.
On considère l’application ![]() .
.
On note ![]() et
et ![]() .
.
![]() Si
Si ![]() est continue sur
est continue sur ![]() et intégrable sur
et intégrable sur ![]() .
.
![]() Si
Si ![]() est de classe
est de classe ![]() et
et ![]() .
.
![]() Si
Si ![]() est continue sur
est continue sur ![]() .
.
![]() Soit
Soit ![]() un segment quelconque inclus dans
un segment quelconque inclus dans ![]() .
.
On note ![]() .
.
… ![]() ,
,
… ![]() est continue sur
est continue sur ![]() .
.
… en choisissant ![]() ,
, ![]() et
et ![]() , donc
, donc ![]() est intégrable sur
est intégrable sur ![]() .
.
… en écrivant ![]() car
car ![]() , on peut alors prolonger
, on peut alors prolonger ![]() par continuité en
par continuité en ![]() en posant
en posant ![]() car
car ![]() .
.
La fonction ![]() est intégrable sur
est intégrable sur ![]() .
.
Par le théorème de dérivabilité des intégrales à paramètre, la fonction ![]() admet une dérivée partielle par rapport à la première variable sur
admet une dérivée partielle par rapport à la première variable sur ![]() et
et
![]() .
.
Pour accéder aux meilleurs cours particuliers à domicile ou en ligne, sélectionner le prof qu'il vous faut

7. Généralisation des intégrales de Wallis
Question 1.
Soit ![]() et
et ![]() . Montrer que
. Montrer que ![]() .
.
Question 2
Montrer que l’on peut définir pour ![]() ,
, ![]() .
.
Montrer que ![]() est de classe
est de classe ![]() sur
sur ![]() . Quel est son sens de variation ?
. Quel est son sens de variation ?
Question 3
Si ![]() , trouver une relation entre
, trouver une relation entre ![]() et
et ![]() .
.
Question 4
Montrer que ![]() est 1-périodique sur
est 1-périodique sur ![]() .
.
Quelle est la valeur de ![]() si
si ![]() ?
?
Question 5
a) Justifier l’équivalence de ![]() et
et ![]() en
en ![]() .
.
b) Montrer que ![]() .
.
Question 6
a) Trouver un équivalent de ![]() lorsque l’entier
lorsque l’entier ![]() tend vers
tend vers ![]() .
.
b) En déduire un équivalent de ![]() lorsque
lorsque ![]() .
.
Corrigé de l’exercice :
Question 1 :
La fonction ![]() définit une bijection strictement croissante de
définit une bijection strictement croissante de ![]() sur
sur ![]() de classe
de classe ![]() .
.
Par le théorème de changement de variable dans l’intégrale ![]() :
:
![]() .
.
soit ![]() .
.
(Faites glisser vers la gauche pour la première valeur de ![]() . )
. )
Question 2 :
a) On remarque que ![]() On peut donc définir
On peut donc définir ![]() car
car ![]() et
et ![]() .
.
On retiendra que ![]() .
.
b) On a prouvé que ![]() est une fonction de classe
est une fonction de classe ![]() et
et ![]() car on intègre une fonction continue sur
car on intègre une fonction continue sur ![]() à valeurs strictement négatives sur
à valeurs strictement négatives sur ![]() .
.
En utilisant ![]() ,
,
![]() est de classe
est de classe ![]() sur
sur ![]() de dérivée à valeurs strictement négatives donc
de dérivée à valeurs strictement négatives donc ![]() est strictement décroissante sur
est strictement décroissante sur ![]() .
.
Question 3 :
Soit ![]() et
et ![]() . On note
. On note ![]() et
et ![]() .
.
![]() et
et ![]() sont de classe
sont de classe ![]() sur
sur ![]() , la fonction
, la fonction ![]() est intégrable sur
est intégrable sur ![]() ,
, ![]() admet 0 pour limite en
admet 0 pour limite en ![]() et
et ![]() car
car ![]() , donc par le théorème d’intégration par parties :
, donc par le théorème d’intégration par parties :
![]() .
.
Puis comme ![]() , on obtient :
, on obtient :
![]() soit
soit ![]() .
.
Question 4 :
Soit ![]() , alors
, alors ![]()
et ![]()
![]() en utilisant la relation de la question précédente, donc
en utilisant la relation de la question précédente, donc ![]() .
.
Alors pour tout ![]() ,
, ![]() .
.
Question 5 :
Si
soit
Par encadrement,
b) On note ![]() .
.
En utilisant l’encadrement ![]() et la décroissance de
et la décroissance de ![]() ,
, ![]() .
.
Si ![]() ,
, ![]() et
et ![]() ,
,
par encadrement par deux suites qui convergent vers ![]() ,
, ![]() soit
soit ![]() .
.
Question 6 :
a) On utilise ![]() et
et ![]() , donc
, donc ![]() .
.
Puis, ![]() et comme
et comme ![]() ,
, ![]() .
.
b) En divisant l’encadrement ![]() par
par ![]() ,
,
par encadrement par deux fonctions de limite égale à 1, on obtient : ![]() .
.
Puis on termine avec la question 5.b) :
![]() donc
donc ![]()
Si vous vous sentez parfaitement à l’aise sur ce chapitre des intégrales à paramètre en Maths Spé, prenez le temps de revoir tranquillement d’autres cours de maths qui vous paraissent un peu plus difficiles, comme par exemple :




