Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Séries entières en MP, PC, PSI, PT
Résumé de cours Exercices et corrigés
Exercices et corrigés – Séries entières
1. Détermination de rayons de convergence
Exercice 1
Déterminer le rayon de convergence ![]() de
de ![]() où
où ![]() .
.
Corrigé de l’exercice 1 :
Si ![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() où
où ![]()
(on a utilisé ![]() ).
).
![]() admet 0 pour limite, donc
admet 0 pour limite, donc ![]() ,
,
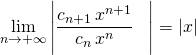
![]() converge si
converge si ![]() et diverge si
et diverge si ![]() , le rayon de convergence de
, le rayon de convergence de ![]() est égal à
est égal à ![]() , par équivalence, le rayon de convergence de
, par équivalence, le rayon de convergence de ![]() est égal à
est égal à ![]() .
.
Exercice 2
Si pour ![]() ,
, ![]() est la somme des carrés des diviseurs de
est la somme des carrés des diviseurs de ![]() , le rayon de convergence
, le rayon de convergence ![]() de
de ![]() vérifie
vérifie
Corrigé de l’exercice 2 :
L’ensemble des diviseurs de ![]() est inclus dans
est inclus dans ![]() .
.
![]() , donc
, donc ![]() .
.
Si ![]() ,
, ![]() , le rayon de convergence de
, le rayon de convergence de ![]() est égal à 1 (utilisation très simple de la règle de d’Alembert), donc le rayon de convergence de
est égal à 1 (utilisation très simple de la règle de d’Alembert), donc le rayon de convergence de ![]() est égal à 1.
est égal à 1.
Grâce à l’encadrement de ![]() à l’aide des termes généraux de deux séries de rayon égal à 1, le rayon de convergence de
à l’aide des termes généraux de deux séries de rayon égal à 1, le rayon de convergence de ![]() est égal à 1.
est égal à 1.
Exercice 3 Mines Ponts MP 2017
Le rayon de convergence ![]() de
de ![]() où
où ![]() est le produit des chiffres de
est le produit des chiffres de ![]() vérifie
vérifie
Corrigé de l’exercice 3 :
![]() On note
On note 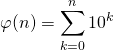 ;
; ![]() .
.
Soit ![]() , la suite
, la suite ![]() est bornée ssi
est bornée ssi ![]() . Si la suite
. Si la suite ![]() est bornée, il en est de même de toute suite extraite, alors
est bornée, il en est de même de toute suite extraite, alors ![]() , donc
, donc ![]() .
.
![]() Soit
Soit ![]() , on introduit
, on introduit ![]() tel que
tel que ![]() , alors
, alors ![]() (cas où
(cas où ![]() est formé de
est formé de ![]() chiffres
chiffres ![]() )
)
![]()
![]()
![]() .
.
En notant ![]() , on a donc prouvé que
, on a donc prouvé que ![]() .
.
On forme : ![]() avec
avec ![]() tend vers
tend vers ![]() , donc
, donc ![]() ,
, 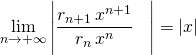 .
.
La série converge si ![]() et diverge si
et diverge si ![]() , le rayon de convergence de
, le rayon de convergence de ![]() est égal à 1, alors le rayon de convergence de
est égal à 1, alors le rayon de convergence de ![]() est supérieur ou égal à 1.
est supérieur ou égal à 1.
![]()
![]() Par double inégalité,
Par double inégalité, ![]() .
.
Exercice 4 Mines Ponts 2018
Justifier l’existence de ![]() et trouver le rayon de convergence de
et trouver le rayon de convergence de ![]() .
.
Corrigé de l’exercice 4 :
![]() Existence de
Existence de ![]()
![]() est continue sur
est continue sur ![]() et vérifie
et vérifie ![]() , donc
, donc ![]() est intégrable par domination par une fonction intégrable sur
est intégrable par domination par une fonction intégrable sur ![]() .
.
![]() Deux changements de variable
Deux changements de variable
![]() On fait un premier changement de variable :
On fait un premier changement de variable :
![]() est une bijection de classe
est une bijection de classe ![]() strictement croissante :
strictement croissante :
![]()
![]() .
.
![]() Puis un deuxième changement de variable :
Puis un deuxième changement de variable :
![]()
est une bijection de classe ![]() strictement croissante :
strictement croissante :
![]() .
.
![]() avec
avec ![]() .
.
![]() Recherche d’un équivalent de
Recherche d’un équivalent de ![]()
On cherche maintenant à utiliser le théorème de convergence dominée :
Soit ![]() .
.
![]()
![]() est continue sur
est continue sur ![]() .
.
![]() la suite
la suite ![]() converge simplement sur
converge simplement sur ![]() vers la fonction continue
vers la fonction continue ![]() .
.
![]() Pour tout
Pour tout ![]() et
et ![]() ,
, ![]() .
.
La fonction ![]() est intégrable sur
est intégrable sur ![]() .
.
Donc par le théorème de convergence dominée, ![]() .
.
![]() Conclusion
Conclusion
On note ![]() .
.
![]() (on intègre une fonction continue positive et différente de la fonction nulle).
(on intègre une fonction continue positive et différente de la fonction nulle).
Alors ![]() , le rayon de convergence de
, le rayon de convergence de ![]() est égal au rayon de convergence de
est égal au rayon de convergence de ![]() soit égal à
soit égal à ![]() .
.
👍 : Soit ![]() et
et ![]() .
.
En présence d’une intégrale convergente ![]() , le changement de variable
, le changement de variable ![]() permet (après justification précise) d’écrire
permet (après justification précise) d’écrire ![]() .
.
Lorsque ![]() est intégrable sur l’intervalle de bornes
est intégrable sur l’intervalle de bornes ![]() et
et ![]() , le théorème de convergence dominée permet de montrer que
, le théorème de convergence dominée permet de montrer que ![]()
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
2. Exercices sur les calculs de sommes de séries
Exercice 5
Convergence et valeur de 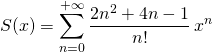 .
.
Corrigé de l’exercice 5 :
![]() Le rayon de convergence est égal à
Le rayon de convergence est égal à ![]() car
car ![]()
et ![]() a même rayon de convergence que
a même rayon de convergence que ![]() .
.
![]() On cherche les réels
On cherche les réels ![]() et
et ![]() tels que
tels que
![]() .
.
En comparant les coefficients de ![]() , on obtient :
, on obtient : ![]() .
.
Puis en prenant les valeurs en ![]() et
et ![]() , on obtient :
, on obtient :
![]() .
.
Comme toutes les séries introduites convergent :
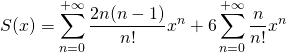
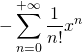
En supprimant les termes nuls :
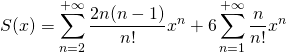
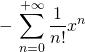
on peut ensuite simplifier :
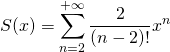
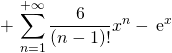
puis par changement d’indices
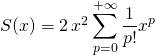
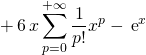
![]() .
.
Exercice 6
Convergence et valeur de ![]() .
.
Corrigé de l’exercice 6
![]() Le rayon de convergence est égal à 1 et la série est absolument convergente en
Le rayon de convergence est égal à 1 et la série est absolument convergente en ![]() .
.
![]()
![]() Calcul de
Calcul de ![]() si
si ![]() .
.
Les deux séries étant convergentes :
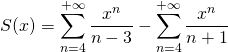 .
.
Par changement d’indices (![]() et
et ![]() ) :
) :
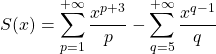 .
.
![]()
![]() .
.
![]() Pour
Pour ![]() ,
,
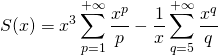
![]()
![]()
![]() avec
avec ![]() .
.
![]() Calcul de
Calcul de ![]() et
et ![]() .
.
La série de fonctions continues de terme général ![]() converge normalement sur
converge normalement sur ![]() car
car ![]() où
où ![]() converge, donc la somme
converge, donc la somme ![]() est continue sur
est continue sur ![]() .
.
![]() ,
,
la relation ![]()
donne ![]() .
.
![]() .
.
Par continuité de ![]() en
en ![]() :
: ![]() .
.
![]() par continuité de
par continuité de ![]() en
en ![]() .
.
Exercice 7 CCP PSI 2017
Convergence et somme de la série entière ![]() avec
avec ![]() .
.
Corrigé de l’exercice 7 :
![]() Rayon de convergence.
Rayon de convergence.
![]() et
et ![]() .
.
Pour tout ![]() .
.
Les rayons de convergence ![]() et
et ![]() des séries
des séries ![]() et
et ![]() vérifient
vérifient ![]() 1, alors
1, alors ![]() = 1 car
= 1 car ![]() .
.
La série de terme général ![]() diverge grossièrement en
diverge grossièrement en ![]() .
.
![]() Calcul de la somme.
Calcul de la somme.
Si ![]() , les séries
, les séries ![]() et
et ![]() étant convergentes, on peut écrire
étant convergentes, on peut écrire 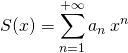 :
:
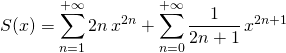
![]() En utilisant :
En utilisant : ![Rendered by QuickLaTeX.com \quad \forall \, t \in \; ] - 1 ,\, 1[,\; \displaystyle \sum _ {n = 1}^ {+\infty} n \, t ^{n - 1} = \frac 1 {( 1 - t)^2}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-8edd39ca94777e8ae190304aa8ef938c_l3.png)
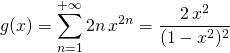 .
.
![]() Si
Si 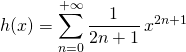 ,
,
par dérivation,
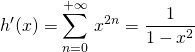
![]()
donc il existe un réel ![]() tel que
tel que
![]()
Comme ![]() ,
, ![]() .
.
Alors pour tout ![]() ,
, ![]() .
.
Tous les chapitres à connaître et à maîtriser parfaitement pour réussir aux concours des meilleures écoles d’ingénieurs sont disponibles gratuitement grâce aux cours en ligne de Maths en PSI, aux cours en ligne de MP en Maths et aux cours en ligne de PC en Maths.
3. Exercices sur les Développement en série entière de fonctions
Exercice 8
Déterminer le DSE de ![]() .
.
Corrigé de l’exercice 8 :
![]()
![]() est de classe
est de classe ![]() sur
sur ![]() et
et
![]() .
.
On pose ![]() et
et ![]() .
.
![]()
puis on cherche ![]() et
et ![]() tels que
tels que
![]() .
.
On obtient facilement ![]()
![]()
ce qui donne ![]() .
.
![]() On transforme
On transforme ![]() de façon à utiliser la série géométrique.
de façon à utiliser la série géométrique.
![]() .
.
![]()
Si ![]() , alors
, alors ![]() et
et ![]() , on peut utiliser le DSE de
, on peut utiliser le DSE de ![]() :
:
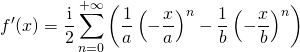
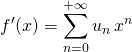
où 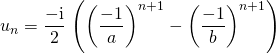
![]() Un peu de calculs dans les complexes pour simplifier l’expression de
Un peu de calculs dans les complexes pour simplifier l’expression de ![]() :
:
![]()
et ![]()
![]()
![]()
![]() .
.
![]() Par intégration d’une série entière sur l’intervalle ouvert de convergence, sans oublier le terme
Par intégration d’une série entière sur l’intervalle ouvert de convergence, sans oublier le terme ![]() ,
,
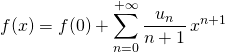
soit 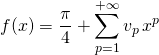
avec ![]() .
.
👍 Les calculs sont nettement plus simples si l’on garde les notations ![]() et
et ![]() plutôt que
plutôt que ![]() et
et ![]() .
.
Aviez vous bien terminé les calculs, c’est-à-dire donné des coefficients de la série entière visiblement réels, puisque ![]() est à valeurs réelles ?
est à valeurs réelles ?
Exercice 9
Montrer que ![]() est DSE et donner ce DSE.
est DSE et donner ce DSE.
Corrigé de l’exercice 9 :
![]() Recherche d’une équation différentielle
Recherche d’une équation différentielle
![]() est deux fois dérivable sur
est deux fois dérivable sur ![]() .
.
![]()
![]()
![]()
soit ![]() .
.
De plus ![]() et
et ![]() .
.
![]() est la seule solution sur
est la seule solution sur ![]() de
de ![]() telle que
telle que ![]() (conséquence du théorème de Cauchy-Lipschitz, à admettre si nécessaire en début d’année).
(conséquence du théorème de Cauchy-Lipschitz, à admettre si nécessaire en début d’année).
![]() Recherche d’une solution DSE de l’équation différentielle
Recherche d’une solution DSE de l’équation différentielle
On cherche une suite ![]() telle que
telle que ![]() ait un rayon de convergence
ait un rayon de convergence ![]() non nul et la fonction définie sur
non nul et la fonction définie sur ![]() par
par 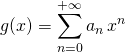 soit solution de l’équation différentielle
soit solution de l’équation différentielle ![]()
et vérifie ![]() et
et ![]() .
.
![]() Si
Si ![]()
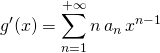 ,
, 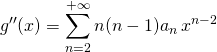
Soit pour ![]() ,
, ![]() .
.
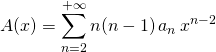
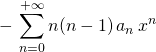
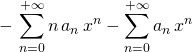
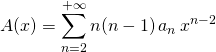
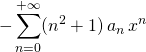
puis avec ![]() ,
,
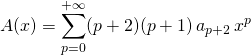
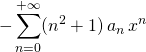 .
.
Par unicité du DSE, la condition ![]() est équivalente à
est équivalente à ![]()
![]() .
.
On détermine les ![]() en utilisant
en utilisant ![]() en distinguant les cas
en distinguant les cas ![]() et
et ![]() .
.
![]()
![]() donne
donne
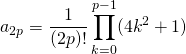 .
.
![]()
![]() donne
donne
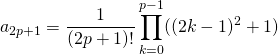 .
.
![]() On détermine le rayon de convergence.
On détermine le rayon de convergence.
![]() si
si ![]() ,
, ![]() ,
, ![]() converge si
converge si ![]() et diverge grossièrement si
et diverge grossièrement si ![]() .
.
![]() si
si ![]() ,
, ![]() ,
, ![]() converge si
converge si ![]() et diverge grossièrement si
et diverge grossièrement si ![]() .
.
![]() Si
Si ![]() , les suites
, les suites ![]() et
et ![]() sont bornées, donc la suite
sont bornées, donc la suite ![]() est bornée.
est bornée.
Si ![]() , les suites
, les suites ![]() et
et ![]() ne sont pas bornées, donc la suite
ne sont pas bornées, donc la suite ![]() n’est pas bornée.
n’est pas bornée.
Le rayon de convergence de ![]() est égal à 1.
est égal à 1.
![]() Conclusion
Conclusion
Il existe une unique fonction ![]() développable en série entière sur
développable en série entière sur ![]() solution de
solution de ![]() et vérifiant
et vérifiant ![]() et
et ![]() .
.
La fonction ![]() est solution sur
est solution sur ![]() de
de ![]() et vérifie
et vérifie ![]() et
et ![]() .
.
On en déduit que ![]() sur
sur ![]() , donc
, donc ![]() est développable en série entière et
est développable en série entière et ![Rendered by QuickLaTeX.com \forall\, x \in ]-1 , \, 1[,\; \displaystyle f(x) = \sum _{n = 0} ^{+\infty} a_n \, x^n](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-7f1ccb63244a9ea9ac77e73aa04b7c14_l3.png) avec
avec
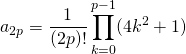
et 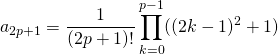 .
.
Exercice 10 Intégrale de Poisson 🧡
Question 1
Soit ![]() . Montrer que
. Montrer que ![]() est définie sur
est définie sur ![]() . La développer en série entière.
. La développer en série entière.
Montrer que le résultat obtenu est encore valable si ![]() où
où ![]() .
.
Question 2
Soit ![]() . Développer en série entière
. Développer en série entière ![]()
![]() .
.
Corrigé de l’exercice 10 :
Question 1 :
![]()
![]() a un discriminant égal à
a un discriminant égal à ![]() donc est à valeurs strictement positives.
donc est à valeurs strictement positives.
![]()
![]() .
.
![]() En décomposant en éléments simples,
En décomposant en éléments simples,
![]()
![]() .
.
![]() En utilisant le DSE de
En utilisant le DSE de ![]() , lorsque
, lorsque ![]() ,
,
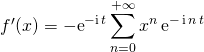
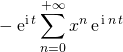 .
.
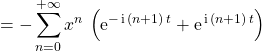
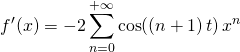 .
.
![]() Alors il existe
Alors il existe ![]() tel que pour tout
tel que pour tout ![]() ,
,
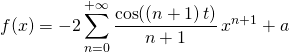
comme ![]() ,
, ![]() donc
donc
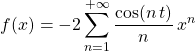 .
.
![]() Lorsque
Lorsque ![]() ,
, ![]() , la relation obtenue est encore vraie.
, la relation obtenue est encore vraie.
![]() Lorsque
Lorsque ![]() ,
, ![]() , la relation obtenue est encore vraie car
, la relation obtenue est encore vraie car ![]() .
.
On en déduit que pour tout réel ![]() et tout
et tout ![]() ,
, 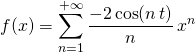 .
.
Question 2 :
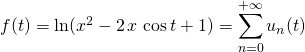 avec
avec 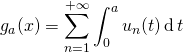
![Rendered by QuickLaTeX.com \displaystyle g_a(x) = \sum_{n = 1} ^{+\infty} \left [ \frac {- 2 \sin(n\,t) } n \, x^n \right ] _{t =0 }^{t = a }](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-7c82840ecb8af29e2134811b034b0087_l3.png)
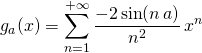 .
.En particulier si
⚠️ Il fallait faire attention à la variable d’intégration ![]() , il ne s’agissait pas d’intégrer terme à terme la somme d’une série entière !
, il ne s’agissait pas d’intégrer terme à terme la somme d’une série entière !
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
4. Fonctions à dérivées positives
Exercice 11 : Mines PSI 2017.
Soit ![]() et
et ![]() une fonction de classe
une fonction de classe ![]() sur
sur ![]() dont toutes les dérivées successives sont positives.
dont toutes les dérivées successives sont positives.
Question 1
Soit ![]() . On note
. On note ![]() le reste intégral de la formule de Taylor écrite à l’ordre
le reste intégral de la formule de Taylor écrite à l’ordre ![]() pour
pour ![]() entre
entre ![]() et
et ![]() .
.
Montrer que la fonction ![]() est croissante sur
est croissante sur ![]() .
.
Question 2
En déduire que ![]() est développable en série entière sur
est développable en série entière sur ![]() .
.
Question 3 Application
Montrer que la fonction ![]() est DSE sur
est DSE sur ![]() .
.
Corrigé de l’exercice 11 :
Question 1 :
![]() Par la formule de Taylor avec reste intégral,
Par la formule de Taylor avec reste intégral, ![]() où
où
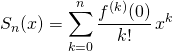 et
et
![]() .
.
En utilisant le changement de variable de classe ![]() défini par :
défini par : ![]() ,
,
![]()
![]()
![]() Si
Si ![]() et
et ![]() ,
, ![]() , la fonction
, la fonction ![]() étant croissante sur
étant croissante sur ![]() ,
,
![]() ,
,
on multiplie par ![]() et on intègre sur
et on intègre sur ![]() :
:
![]()
![]()
soit ![]() .
.![]()
![]() La fonction
La fonction ![]() est croissante sur
est croissante sur ![]() .
.
Question 2 :
Soit ![]() et
et ![]() , alors
, alors ![]() , donc
, donc ![]() .
.
Puis comme ![]() car
car ![]()
![]() .
.
Comme ![]() , par encadrement,
, par encadrement, ![]() .
.
On a prouvé que ![]() .
.
![]() est développable en série entière sur
est développable en série entière sur ![]() .
.
Question 3 :
La fonction ![]() est de classe
est de classe ![]() sur
sur ![]() .
.
On va démontrer que ![]() est à valeurs positives sur
est à valeurs positives sur ![]() .
.
On note ![]() :
: ![]() où
où ![]() est une fonction polynôme à coefficients dans
est une fonction polynôme à coefficients dans ![]() .
.
La propriété est vraie pour ![]() avec
avec ![]()
On suppose qu’elle est vraie au rang ![]() .
.
Pour ![]()
![]()
![]() où
où ![]() est un polynôme à coefficients dans
est un polynôme à coefficients dans ![]() .
.
On en déduit que ![]() .
.
Par application de la deuxième question,![]() est développable en série entière sur
est développable en série entière sur ![]() .
.
Par parité, la relation obtenue est alors valable sur ![]() .
.
Les sujets de concours post-prépa font appel à l’ensemble des notions de mathématiques de Maths Spé, une connaissance parfaite de tous les chapitres du programme est donc requise. Pour vous aider voici une partie des chapitres à connaître par cœur :
- le dénombrement
- les intégrales à paramètre
- les variables aléatoires
- les probabilités
- les espaces préhilbertiens
Pour avoir les corrigés de tous ces exercices et accéder à tous les exercices et annales corrigés, n’hésitez pas à télécharger l’application mobile PrepApp.

