Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Suites et séries de fonctions en MP, PC, PSI
Résumé de cours Exercices et corrigés
Exercices et corrigés – Suites et séries de fonctions
1. Études de convergence de suites
Exercice 1
Soit la suite de fonctions définies pour ![]() par
par ![]() sur
sur ![]() et
et ![]() si
si ![]() .
.
Étudier de la convergence simple puis uniforme.
Corrigé de l’exercice 1 :
![]() Étude de la convergence simple
Étude de la convergence simple
![]() donc
donc ![]() .
.
Si ![]() , il existe
, il existe ![]() tel que
tel que ![]() , alors si
, alors si ![]() ,
, ![]() ,
, ![]()
![]() .
.
La suite ![]() converge simplement vers la fonction nulle.
converge simplement vers la fonction nulle.
On remarquera la discontinuité de ![]() en
en ![]() .
.
![]() Étude de la convergence uniforme
Étude de la convergence uniforme
Sur ![]() ,
, ![]() est croissante et varie de 0 à
est croissante et varie de 0 à ![]() .
.
Sur ![]() ,
, ![]() est décroissante (calculer la dérivée sur l’intervalle ouvert) et varie de 0 à
est décroissante (calculer la dérivée sur l’intervalle ouvert) et varie de 0 à ![]() .
.
alors ![]()
![]() ,
,
![]() . alors la suite converge uniformément sur
. alors la suite converge uniformément sur ![]() vers la fonction nulle.
vers la fonction nulle.
⚠️ : il est absurde de donner une réponse du type si ![]() converge vers …
converge vers …
Exercice 2
![]() .
.
Question 1
Étude de la convergence simple et uniforme de la suite ![]() .
.
Question 2
Montrer que la limite ![]() est dérivable mais que la suite
est dérivable mais que la suite ![]() ne converge pas vers
ne converge pas vers ![]() sur
sur ![]() .
.
Corrigé de l’exercice 2 :
Question 1 :
![]() Étude de la convergence simple
Étude de la convergence simple
![]()
![]() tend vers 0.
tend vers 0.
![]() Si
Si ![]() .
.
La suite ![]() converge simplement sur
converge simplement sur ![]() vers la fonction
vers la fonction ![]() .
.
![]() Étude de la convergence uniforme
Étude de la convergence uniforme
Soit pour ![]() ,
, ![]()
![]() .
.
![]() est croissante sur
est croissante sur ![]() et décroissante sur
et décroissante sur ![]() ,
, ![]() ,
, ![]() ,
, ![]() admet 0 pour limite en
admet 0 pour limite en ![]() .
.
Donc ![]() .
.
Donc la suite ![]() converge uniformément vers la fonction
converge uniformément vers la fonction ![]() sur
sur ![]() .
.
Question 2 :
Il est évident que ![]() est dérivable sur
est dérivable sur ![]() et
et ![]() .
.
![]() .
.
![]() , cette suite ne converge pas vers
, cette suite ne converge pas vers ![]() . La suite
. La suite![]() ne converge pas simplement vers
ne converge pas simplement vers ![]() .
.
Exercice 3
Pour ![]() ,
, ![]() sur
sur ![]() .
.
Question 1
Étude de la convergence simple puis uniforme de la suite.
Question 2
Déterminer ![]() .
.
Corrigé de l’exercice 3 :
Question 1 :
![]() Étude de la convergence simple
Étude de la convergence simple
![]() , la suite
, la suite ![]() converge vers 0.
converge vers 0.
Si ![]() , la suite
, la suite ![]() converge vers 0, donc
converge vers 0, donc ![]() , puis par croissance comparée,
, puis par croissance comparée, ![]() , la suite
, la suite ![]() converge simplement vers la fonction nulle sur
converge simplement vers la fonction nulle sur ![]() .
.
![]() Étude de la convergence uniforme
Étude de la convergence uniforme
![]()
On utilise ![]() , donc
, donc ![]() .
.
Comme ![]() ,
, ![]() ne converge pas vers 0, car elle est supérieure à une suite de limite égale à
ne converge pas vers 0, car elle est supérieure à une suite de limite égale à ![]() . Il n’y a pas de convergence uniforme.
. Il n’y a pas de convergence uniforme.
Question 2 :
En utilisant si ![]() et
et ![]()
![]()
![]()
![]() .
.
Donc ![]() .
.
2. Exercices théoriques sur les suites et séries de fonctions
Exercice 4
Soit ![]() une suite de fonctions définies sur
une suite de fonctions définies sur ![]() à valeurs dans
à valeurs dans ![]() .
.
Question 1
Si la suite ![]() converge uniformément sur
converge uniformément sur ![]() et si la suite
et si la suite ![]() converge, la suite
converge, la suite ![]() converge uniformément sur
converge uniformément sur ![]()
Question 2
Si la suite ![]() converge uniformément sur
converge uniformément sur ![]() et si toutes les fonctions
et si toutes les fonctions ![]() sont continues sur
sont continues sur ![]() , la suite
, la suite ![]() converge uniformément sur
converge uniformément sur ![]() ?
?
Question 3
Si la suite ![]() converge uniformément sur tout segment de
converge uniformément sur tout segment de ![]() , si toutes les fonctions
, si toutes les fonctions ![]() sont continues sur
sont continues sur ![]() et si la suite
et si la suite ![]() converge, la suite
converge, la suite ![]() converge uniformément sur
converge uniformément sur ![]()
Corrigé de l’exercice 4 :
Question 1 :
Comme la suite ![]() converge uniformément vers
converge uniformément vers ![]() sur
sur ![]() :
:
![]()
![]() .
.
et comme la suite ![]() converge vers
converge vers ![]() :
: ![]() .
.
On note ![]() et on en déduit que si
et on en déduit que si ![]() , si
, si ![]() ,
, ![]() , donc
, donc ![]() .
.
On en déduit que ![]() converge uniformément vers
converge uniformément vers ![]() sur
sur ![]() .
.
Question 2 :
La suite ![]() converge uniformément vers
converge uniformément vers ![]() sur
sur ![]() .
.
Pour tout ![]() , par continuité de
, par continuité de ![]() sur
sur ![]() ,
, ![]() admet une limite finie en
admet une limite finie en ![]() .
.
Par application du théorème de la double limite ,
![]() soit
soit ![]() .
.
On peut donc appliquer la question 1, puisque la suite ![]() converge, donc la suite
converge, donc la suite ![]() converge uniformément sur
converge uniformément sur ![]() .
.
Question 3 :
Si l’on note ![]() ,
,
Si ![]() , donc la suite
, donc la suite ![]() converge uniformément sur tout segment de [0 ,\, 1[,
converge uniformément sur tout segment de [0 ,\, 1[,
La suite ![]() est une suite constante égale à
est une suite constante égale à ![]() , elle converge.
, elle converge.
Mais la suite ![]() ne converge pas uniformément sur
ne converge pas uniformément sur ![]() , car sa limite est une fonction discontinue, alors que chaque fonction
, car sa limite est une fonction discontinue, alors que chaque fonction ![]() est continue sur
est continue sur ![]() .
.
Exercice 5
Soit ![]() une suite de fonctions définies sur
une suite de fonctions définies sur ![]() à valeurs dans
à valeurs dans ![]() .
.
On suppose que la suite ![]() converge uniformément sur
converge uniformément sur ![]() .
.
Soit ![]() une fonction continue sur
une fonction continue sur ![]() à valeurs dans
à valeurs dans ![]() .
.
La suite ![]() converge uniformément sur
converge uniformément sur ![]() .
.
Corrigé de l’exercice 5 :
On note ![]() la limite uniforme de
la limite uniforme de ![]() sur
sur ![]() .
.
Pour tout ![]() ,
, ![]() , par passage à la limite dans l’encadrement pour tout
, par passage à la limite dans l’encadrement pour tout ![]() ,
, ![]() .
.
![]() est continue sur
est continue sur ![]() donc uniformément continue.
donc uniformément continue.
![]() tel que si
tel que si ![]() et
et ![]() ,
, ![]() .
.
Comme ![]() , il existe
, il existe ![]() .
.
Pour tout ![]() , donc
, donc ![]() , soit
, soit ![]() .
.
On a donc prouvé que ![]() converge uniformément vers
converge uniformément vers ![]() sur
sur ![]() .
.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
3. Théorème de Weierstrass
Exercice 6 🧡
Soit ![]() une fonction continue sur
une fonction continue sur ![]() à valeurs dans
à valeurs dans ![]() telle que
telle que ![]() . Alors la fonction
. Alors la fonction ![]() est nulle sur
est nulle sur ![]() .
.
Corrigé de l’exercice 6 :
Par combinaison linéaire, pour tout polynôme ![]() :
: ![]() .
.
Par le théorème de Weirstrass, il existe une suite ![]() de fonctions polynomiales telle que
de fonctions polynomiales telle que ![]() .
.
![]()
![]()
donc ![]()
La suite ![]() converge uniformément vers
converge uniformément vers ![]() sur
sur ![]() . On en déduit que
. On en déduit que
![]() .
.
Par unicité de la limite, ![]() .
.
La fonction ![]() étant continue sur
étant continue sur ![]() , à valeurs positives ou nulles et d’intégrale nulle sur
, à valeurs positives ou nulles et d’intégrale nulle sur ![]() ,
,
![]() .
.
Exercice 7 Mines Ponts 2013.
Soit ![]() . Soit
. Soit ![]() une suite d’éléments de
une suite d’éléments de ![]() convergeant uniformément vers une fonction
convergeant uniformément vers une fonction ![]() . Démontrer que
. Démontrer que ![]() est polynomiale.
est polynomiale.
Corrigé de l’exercice 7 :
On suppose que ![]() est une suite d’éléments de
est une suite d’éléments de ![]() convergeant uniformément vers une fonction
convergeant uniformément vers une fonction ![]() .
.
Soit ![]() . Il existe
. Il existe ![]() , tel que si
, tel que si ![]() ,
, ![]() .
.
![]()
![]()
![]() est une fonction polynôme bornée sur
est une fonction polynôme bornée sur ![]() , donc elle est constante.
, donc elle est constante.
Il existe ![]() tel que
tel que
![]() ,
, ![]() .
.
Puis ![]() ,
,
donc ![]() ; si
; si ![]() tend vers
tend vers ![]() ,
, ![]() .
.
![]() est une fonction polynomiale.
est une fonction polynomiale.
Tous nos cours en ligne ont pour unique objectif de faciliter l’apprentissage et d’améliorer le niveau de connaissances des étudiants de Maths Spé. Tous les chapitres du programme sont disponibles en cours en ligne de Maths en MP, en cours en ligne de Maths en PC et aussi en cours en ligne de Maths en PSI.
4. Convergence simple, normale, uniforme
Exercice 8 :
Soit ![]() où
où ![]() .
.
Question 1.
La série converge simplement sur quel domaine ?
Question 2
La série converge-t-elle normalement sur ![]() ?
?
Question 3
Pour tout ![]() ,
, ![]() converge normalement sur
converge normalement sur ![]() .
.
Question 4
La série ne converge pas uniformément sur ![]() .
.
Question 5
La somme ![]() est continue sur
est continue sur ![]() et admet une limite finie en
et admet une limite finie en ![]()
Question 6
La fonction ![]() n’est pas continue en
n’est pas continue en ![]() .
.
Question 7
Montrer que ![]() .
.
Question 8 (plus compliquée)
a) Soit ![]() , on note
, on note ![]() .
.
Montrer que ![]() .
.
Dans les questions b) et c), on fixe![]() .
.
Soit pour ![]() et
et ![]() .
.
b) Montrer que 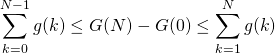 .
.
c) Montrer que 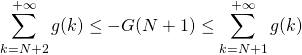 .
.
d) En déduire un encadrement de ![]() puis la limite de
puis la limite de ![]() à droite en
à droite en ![]() .
.
Corrigé de l’exercice 8 :
Question 1:
![]() Si
Si ![]() , donc
, donc ![]() diverge grossièrement
diverge grossièrement
![]() Si
Si ![]() , la série converge.
, la série converge.
![]() Si
Si ![]() ,
, ![]() , donc
, donc ![]() , la série de terme général
, la série de terme général ![]() converge par domination par une série de Riemann divergente.
converge par domination par une série de Riemann divergente.
Donc la série de terme général ![]() converge simplement sur
converge simplement sur ![]() .
.
Question 2 :
Si ![]() ,
, ![]() .
.
![]() est croissante sur
est croissante sur ![]() , décroissante sur
, décroissante sur ![]() ,
, ![]() admet un maximum en
admet un maximum en ![]() et
et ![]()
et ![]() puisque
puisque ![]() est à valeurs positives ou nulles sur
est à valeurs positives ou nulles sur ![]() .
.
La série ne converge pas normalement sur ![]() .
.
Question 3 :
donc
Question 4 :
Si ![]() .
. 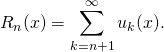
Comme les fonctions sont à valeurs positives ou nulles, 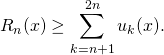
Comme on somme ![]() termes tous supérieurs ou égaux à
termes tous supérieurs ou égaux à ![]() ,
,
![]()
![]()
donc ![]() . La suite de terme général
. La suite de terme général ![]() ne converge pas uniformément vers 0.
ne converge pas uniformément vers 0.
On en déduit que la série ne converge pas uniformément sur ![]() .
.
Question 5 :
![]() La série
La série ![]() converge normalement donc uniformément sur
converge normalement donc uniformément sur ![]() pour tout
pour tout ![]() donc converge uniformément sur tout segment inclus dans
donc converge uniformément sur tout segment inclus dans ![]() , les fonctions
, les fonctions ![]() sont continues, par le théorème de continuité des sommes de séries de fonctions, la somme
sont continues, par le théorème de continuité des sommes de séries de fonctions, la somme ![]() de la série est continue sur
de la série est continue sur ![]() .
.
![]() Étude de la limite en
Étude de la limite en ![]()
![]() La série
La série ![]() converge normalement donc uniformément sur
converge normalement donc uniformément sur ![]() .
.
![]() Pour tout
Pour tout ![]() ,
, ![]() .
.
Par le théorème de la double limite, ![]() .
.
Question 6 :
Pour tout ![]() ,
, 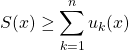 .
.
Donc 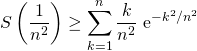
Comme ![]()
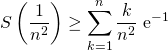
soit ![]()
La suite ![]() est supérieure à une suite de limite strictement positive, donc elle ne converge pas vers
est supérieure à une suite de limite strictement positive, donc elle ne converge pas vers ![]() , donc
, donc ![]() n’est pas continue en
n’est pas continue en ![]() .
.
Question 7 :
![]() La série de terme général
La série de terme général ![]() converge normalement sur
converge normalement sur ![]() et pour tout
et pour tout ![]() ,
, ![]() admet 0 pour limite en
admet 0 pour limite en ![]() .
.
Par le théorème de la double limite, ![]() admet
admet ![]() pour limite en
pour limite en ![]() .
.
![]() . On écrit
. On écrit ![]() avec
avec 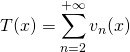 où
où ![]() .
.
![]() Pour tout
Pour tout ![]() .
.
![]() La fonction
La fonction ![]() est décroissante sur
est décroissante sur ![]() , à valeurs positives,
, à valeurs positives,
![]() .
.
Comme ![]() si
si ![]() ,
, ![]() qui est le terme général d’une série géométrique convergente.
qui est le terme général d’une série géométrique convergente.
Donc ![]() converge normalement sur
converge normalement sur ![]() .
.
![]() Par le théorème de la double limite,
Par le théorème de la double limite, ![]() et on a prouvé que
et on a prouvé que ![]() .
.
Question 8 :
a/ On utilise ![]() donc
donc ![]() et alors
et alors ![]() , donc
, donc ![]() .
.
On peut aussi écrire que ![]() .
.
b/
On remarque que ![]() est une primitive de
est une primitive de ![]() .
.
![]() Si
Si ![]() ,
, ![]() .
.
![]() .
.
Soit ![]() ,
, ![]() est croissante sur
est croissante sur ![]() et décroissante sur
et décroissante sur ![]() .
.
![]() Si
Si ![]()
![]() .
.
En intégrant sur ![]() ,
, ![]() .
.
![]() Puis en sommant pour
Puis en sommant pour ![]() , par la relation de Chasles,
, par la relation de Chasles,
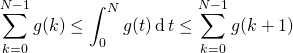
soit
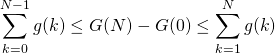 .
.
c/ ![]() Si
Si ![]()
![]() .
.
En intégrant sur ![]() ,
, ![]() .
.
![]() Puis en sommant pour
Puis en sommant pour ![]() , par la relation de Chasles,
, par la relation de Chasles,
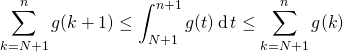
soit ![Rendered by QuickLaTeX.com \displaystyle \sum_{k = N + 2 } ^{n + 1 } g(k) \leq \left [ G(t) \right] _{N + 1}^{n + 1} \leq \sum _{k = N + 1 } ^{n} g(k)](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-c47a1c59304d60ade137e34e111c545f_l3.png) .
.
![]() Puis si
Puis si ![]() tend vers
tend vers ![]() , comme
, comme ![]() admet 0 pour limite en
admet 0 pour limite en ![]() ,
,
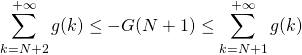 .
.
d/ En sommant les inégalités des questions b) et c), sachant que 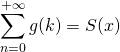 ,
,
![]()
![]()
Ce qui donne un encadrement ![]() avec
avec ![]() et
et ![]()
![]()
![]()
Sachant que ![]() ,
,![]()
![]() et
et ![]() .
.
![]() Puis comme
Puis comme ![]() ,
, ![]() , donc
, donc ![]() .
.
Il en est de même de ![]() .
.
Alors ![]() .
.
![]() Par encadrement par deux expressions ayant même limite
Par encadrement par deux expressions ayant même limite ![]() lorsque
lorsque ![]() , on a donc prouvé
, on a donc prouvé ![]() .
.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
5. Série de fonctions définie à l’aide d’intégrales
Exercice 9 :
(Mines Ponts PSI 2017)
Soit ![]() une fonction continue de
une fonction continue de ![]() dans
dans ![]() . On définit la suite
. On définit la suite ![]() par :
par : ![]() .
.
Question 1
Étudier la convergence uniforme sur tout segment de ![]() .
.
On note 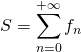 .
.
Question 2
Déterminer ![]() à l’aide d’une équation différentielle.
à l’aide d’une équation différentielle.
Corrigé de l’exercice 9 :
Question 1 :
![]() Par récurrence immédiate, pour tout
Par récurrence immédiate, pour tout ![]() est continue sur
est continue sur ![]() .
.
![]() Soit
Soit ![]() . On note
. On note ![]() .
.
On note ![]() .
.
![]()
![]() est vraie par définition de
est vraie par définition de ![]() .
.
![]() On suppose que
On suppose que ![]() est vraie.
est vraie.
Si ![]()
![]()
… Si ![]() ,
, ![]() .
.
… Si ![]() ,
, ![]()
![]()
![]()
![]() .
.
On a obtenu dans les deux cas : ![]() .
.
La propriété ![]() est vérifiée.
est vérifiée.
![]() Alors
Alors ![]() .
.
Par domination par une série convergente (de somme exponentielle) la série de terme général ![]() converge donc
converge donc ![]() converge normalement donc uniformément sur
converge normalement donc uniformément sur ![]() .
.
Question 2 :
![]() On note
On note ![]() la somme de la série. La fonction
la somme de la série. La fonction ![]() est une fonction continue sur
est une fonction continue sur ![]() comme limite uniforme sur tout segment d’une série de fonctions continues.
comme limite uniforme sur tout segment d’une série de fonctions continues.
![]() Soit
Soit ![]() ,
, 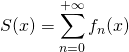 .
.
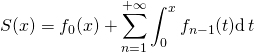 .
.
La série converge normalement sur tout segment, on peut donc intervertir le signe ![]() et l’intégrale :
et l’intégrale :
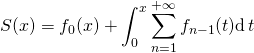 .
.
![]() .
.
Par le théorème fondamental de l’intégration, la fonction ![]() est une fonction de classe
est une fonction de classe ![]() telle que
telle que ![]() .
.
De plus, ![]() .
.
![]() On résout l’équation différentielle
On résout l’équation différentielle ![]() .
.
![]() La solution générale de l’équation sans second membre est
La solution générale de l’équation sans second membre est ![]() où
où ![]() .
.
![]() Par la méthode de variation de la constante, la fonction
Par la méthode de variation de la constante, la fonction ![]() est solution de l’équation différentielle ssi
est solution de l’équation différentielle ssi
![]()
![]()
![]()
![]()
Soit ![]() ,
, ![]() est une solution particulière de l’équation différentielle.
est une solution particulière de l’équation différentielle.
![]() La solution générale de l’équation
La solution générale de l’équation ![]() est donnée par
est donnée par ![]() où
où ![]() .
.
Et comme on cherche la solution ![]() telle que
telle que ![]() , on obtient
, on obtient ![]() et
et ![]() .
.
Donc ![]()
6. Recherche d’un équivalent en une borne de l’intervalle
Exercice 10 (Zeta) 🧡
Soit si 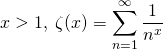 .
.
Montrer que ![]() .
.
Corrigé de l’exercice 10 :
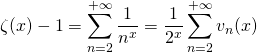 où
où ![]()
On note 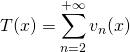
![]()
![]() et
et ![]() .
.
![]() Si
Si ![]() et
et ![]() ,
, ![]() car la fonction
car la fonction ![]() est décroissante sur
est décroissante sur ![]() .
.
donc ![]() qui est le terme général d’une série convergente.
qui est le terme général d’une série convergente.
![]() Par le théorème de la double limite,
Par le théorème de la double limite, ![]() , on a donc prouvé que
, on a donc prouvé que ![]() .
.
Un bon niveau en Maths s’acquiert par des révisions de cours mais aussi par des entraînements sur des exercices de cours. Testez-vous et vérifiez vos connaissances sur les cours en ligne et les exercices corrigés de Maths Spé suivants :
- l’intégration sur un intervalle quelconque
- les séries entières
- le dénombrement
- les intégrales à paramètre
- les variables aléatoires
Pour avoir les corrigés de tous ces exercices et accéder à tous les exercices et annales corrigés, n’hésitez pas à télécharger l’application mobile PrepApp.

