Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Variables aléatoires en MP, PC, PSI et PT
Résumé de cours Exercices et corrigés
Exercices et corrigés – Variables aléatoires
1. Loi géométrique : min, max etc …
Soient ![]() et
et ![]() deux variables aléatoires suivant des lois géométriques de paramètres
deux variables aléatoires suivant des lois géométriques de paramètres ![]() et
et ![]() (
(![]() ).
).
Soit ![]() et
et ![]() .
.
Question 1.
Déterminer la loi conjointe du couple ![]() .
.
Question 2
![]() suit une loi géométrique de paramètre
suit une loi géométrique de paramètre
Question 3
Pour tout ![]() ,
, ![]()
Question 4
![]() et
et ![]() sont indépendantes
sont indépendantes
Question 5
Soit ![]() .
.
De la loi de ![]() , on peut déduire la loi de
, on peut déduire la loi de ![]() . Si oui, la donner.
. Si oui, la donner.
Question 6
Déterminer la loi de ![]() .
.
Corrigé de l’exercice :
Question 1 :
On note dans la suite ![]() et
et ![]() .
. ![]() et
et ![]() .
.
![]() Si
Si ![]() ,
, ![]()
![]()
![]() car
car ![]() et
et ![]() sont indépendantes.
sont indépendantes.
![]() .
.
![]() Si
Si ![]() ,
,
![]()
![]()
![]()
![]()
![]()
et par indépendance de ![]() et
et ![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
STAGE INTENSIF EN MATHS SPÉ
Profite de tes vacances pour gagner des points aux concours.
100% obtiennent une école d’ingénieur
58% admissibles Mines-Centrales
99% de recommandation à leurs amis
Avis Google France ★★★★★ 4,9 sur 5
Question 2 :
On détermine la loi de ![]() comme loi marginale du couple :
comme loi marginale du couple :
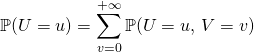
On distingue le cas ![]() de
de ![]() .
.
![]()
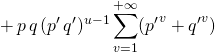 .
.
![]()
![]() .
.
![]() et
et ![]() donnent la simplification :
donnent la simplification :
![]()
On calcule : ![]()
![]() .
.
On a montré que pour tout ![]() ,
,
![]()
avec ![]() .
.
![]() suit une loi géométrique de paramètre
suit une loi géométrique de paramètre ![]() .
.
Question 3 :
La propriété est fausse si ![]() mais vraie si
mais vraie si ![]() .
.
![]()
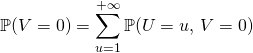
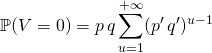
![]()
![]() Si
Si ![]() ,
,
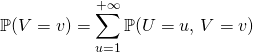
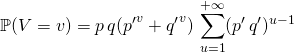
![]()
![]()
Question 4 :
Soit
Si
et
donc pour tout
![]()
![]() et
et ![]() sont des variables aléatoires indépendantes.
sont des variables aléatoires indépendantes.
Question 5 :
On utilise ![]() .
.
Donc si ![]() ,
,
![]()
![]() si
si ![]() ,
, ![]() .
.
![]() si
si ![]() ,
, ![]()
![]() .
.
![]() si
si ![]() ,
, ![]()
![]()
où ![]() et
et ![]() .
.
Question 6 :
Pour déterminer la loi de ![]() , on calcule
, on calcule ![]()
Par indépendance de ![]() et
et ![]() ,
,
![]() .
.
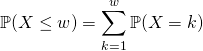
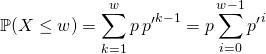
![]() .
.
![]()
La propriété reste vraie si ![]() .
.
On écrit ensuite si ![]() ,
, ![]() .
.
Ces événements étant incompatibles :
![]()
donc
![]()
![]()
![]()
![]() .
.
Pour accéder aux meilleurs cours particuliers à domicile ou en ligne, sélectionner le prof qu'il vous faut

2. Somme de variables indépendantes de loi géométrique
Annale Mines Ponts MP 2018
Question 1.
On considère ![]() variables aléatoires indépendantes qui suivent une loi géométrique de paramètre
variables aléatoires indépendantes qui suivent une loi géométrique de paramètre ![]() . Soit
. Soit ![]() .
.
La somme ![]() de ces
de ces ![]() variables aléatoires vérifie si
variables aléatoires vérifie si ![]()
a) ![]()
b) ![]()
c) ![]()
d) ![]()
Question 2.
Une bactérie a une probabilité ![]() de se faire toucher par un laser et il faut
de se faire toucher par un laser et il faut ![]() coups de laser pour la tuer. Calculer la loi de
coups de laser pour la tuer. Calculer la loi de ![]() , temps de vie de la bactérie, et son espérance sachant qu’il y a 1 seconde entre chaque passage de laser.
, temps de vie de la bactérie, et son espérance sachant qu’il y a 1 seconde entre chaque passage de laser.
a) ![]()
b) ![]()
c) ![]()
d) ![]() .
.
Corrigé de l’exercice :
Question 1 :
![]() La fonction génératrice
La fonction génératrice ![]() d’une variable aléatoire de loi géométrique de paramètre
d’une variable aléatoire de loi géométrique de paramètre ![]() est définie sur
est définie sur ![]() par
par ![]() en notant
en notant ![]() .
.
La fonction génératrice d’une somme de ![]() variables aléatoires indépendantes est égale au produit des fonctions génératrices, donc la fonction génératrice de
variables aléatoires indépendantes est égale au produit des fonctions génératrices, donc la fonction génératrice de ![]() est définie sur
est définie sur ![]() par
par ![]() .
.
![]() En dérivant
En dérivant ![]() fois la relation
fois la relation ![Rendered by QuickLaTeX.com \quad \forall\, u \in \; ]-1, \, 1[,\; \displaystyle \frac 1 {1 - u} = \sum _ {k = 0} ^{+\infty} u ^k](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-8086eccc5df4ce3ee919eb2b2ca25268_l3.png) ,
,
on obtient
![]()
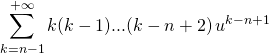 ,
,
En divisant par ![]() , on obtient
, on obtient
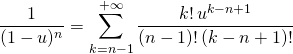
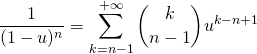 .
.
![]() Alors
Alors ![]() est égal à
est égal à
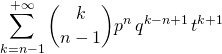
Puis en posant ![]() ,
,
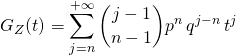 .
.
Par unicité du DSE,
si ![]() et si
et si ![]() .
.
Question 2 :
On obtient ![]() .
.
Soit ![]() où
où ![]() « la bactérie est touchée à la seconde
« la bactérie est touchée à la seconde ![]() » et
» et ![]() « en
« en ![]() secondes, la bactérie a été touchée
secondes, la bactérie a été touchée ![]() fois et non touchée
fois et non touchée ![]() fois ».
fois ».
![]()
![]() car
car ![]() où
où ![]() suit une loi binomiale de paramètres
suit une loi binomiale de paramètres ![]() .
.
![]() .
.
On remarque que ![]() a même loi que la somme de
a même loi que la somme de ![]() variables aléatoires
variables aléatoires ![]() indépendantes de loi géométrique de paramètre
indépendantes de loi géométrique de paramètre ![]() .
.
Alors 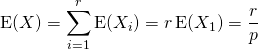 .
.
L’ensemble des chapitres de mathématiques qui sont au programme de Maths Spé sont disponibles en cours en ligne. Révisez le chapitre sur lequel vous souhaitez progresser parmi les cours en ligne de Maths en PC, les cours en ligne de Maths en MP et les cours en ligne de Maths en PSI.
3. Problème du collectionneur
CCP MP 2018 – Mines Ponts PSI 2015
On cherche à obtenir toutes les pièces d’un puzzle de ![]() pièces différentes.
pièces différentes.
On achète chaque semaine une pièce emballée, chaque pièce étant équiprobable. On note ![]() la variable aléatoire égale au nombre de semaines nécessaires pour avoir une
la variable aléatoire égale au nombre de semaines nécessaires pour avoir une ![]() -ième nouvelle pièce à partir du moment où l’on en a déjà
-ième nouvelle pièce à partir du moment où l’on en a déjà ![]() .
.
Question 1
a) Quelle est la loi de ![]() ? Quelle est celle de
? Quelle est celle de ![]() si
si ![]() ?
?
b) Les variables ![]() sont-elles mutuellement indépendantes ?
sont-elles mutuellement indépendantes ?
c) Donner l’espérance et la variance de ![]() si
si ![]()
Question 2
On introduit ![]() la variable aléatoire comptant le nombre d’achats nécessaires pour avoir les
la variable aléatoire comptant le nombre d’achats nécessaires pour avoir les ![]() pièces différentes du puzzle.
pièces différentes du puzzle.
a) Si 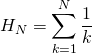 , l’espérance de
, l’espérance de ![]() est égale à
est égale à
R1 : ![]() R2 :
R2 : ![]()
b) En utilisant une comparaison série-intégrale, on démontre que ![]() .
.
c) L’espérance de ![]() est équivalente à
est équivalente à ![]() si
si ![]() .
.
d) Il existe un équivalent de ![]() lorsque
lorsque ![]() de la forme
de la forme ![]() .
.
Corrigé de l’exercice :
Question 1 :
a/ ![]() est la variable aléatoire certaine égale à 1.
est la variable aléatoire certaine égale à 1.
Si ![]() ,
, ![]() est le temps d’attente du premier succès lors d’une suite d’épreuves indépendantes de probabilité de succès égale à
est le temps d’attente du premier succès lors d’une suite d’épreuves indépendantes de probabilité de succès égale à ![]() .
.
![]() suit une loi géométrique :
suit une loi géométrique : ![]() et pour tout
et pour tout ![]()
![]() .
.
b/
On démontre que les variables sont mutuellement indépendantes :
Si ![]() et si
et si ![]() , avec
, avec ![]() , on note
, on note ![]()
![]() .
.
Réaliser 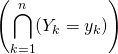 revient
revient
![]() à obtenir la même pièce du rang 1 au rang
à obtenir la même pièce du rang 1 au rang ![]() de probabilité
de probabilité ![]()
![]() à obtenir une nouvelle pièce au rang
à obtenir une nouvelle pièce au rang ![]() de probabilité
de probabilité ![]()
![]() à obtenir une des deux pièces déjà obtenues du rang
à obtenir une des deux pièces déjà obtenues du rang ![]() au rang
au rang ![]() soit
soit ![]() fois de probabilité
fois de probabilité ![]()
![]() à obtenir une nouvelle pièce au rang
à obtenir une nouvelle pièce au rang ![]() de probabilité
de probabilité ![]() ,
,
….
![]() obtenir une des
obtenir une des ![]() pièces déjà obtenues du rang
pièces déjà obtenues du rang ![]() au rang
au rang ![]() soit
soit ![]() fois de probabilité
fois de probabilité ![]()
![]() obtenir une nouvelle pièce au rang
obtenir une nouvelle pièce au rang ![]() de probabilité
de probabilité ![]() .
.
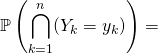
![]()
![]() .
.
On a vu que si ![]()
![]() .
.
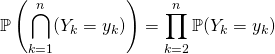 ,
,
soit aussi
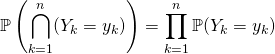 .
.
car ![]() .
.
On a prouvé l’indépendance des v.a.r. ![]() pour tout
pour tout ![]() tel que
tel que ![]() , donc les variables
, donc les variables ![]() sont mutuellement indépendantes.
sont mutuellement indépendantes.
c/
Par propriété des lois géométriques,
![]()
et ![]() .
.
Ces résultats sont encore vrais si ![]() .
.
COURS PARTICULIERS EN CPGE MATHS SPE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers pour les élèves de Maths Spé
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Question 2 :
a/
Il est évident que 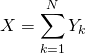 donc par linéarité de l’espérance,
donc par linéarité de l’espérance, 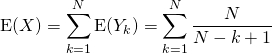 .
.
et en posant ![]() ,
,
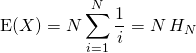 .
.
b/
Par division par ![]() ,
,
![]()
donc par encadrement :
![]()
et alors ![]() .
.
c/
![]() .
.
d/
Comme les variables ![]() sont indépendantes,
sont indépendantes, 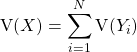 .
.
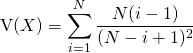
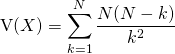 .
.
en posant ![]() . Donc :
. Donc :
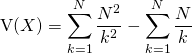 .
.
On note 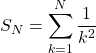 . La suite
. La suite ![]() converge vers
converge vers 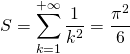 .
.
![]()
et ![]() .
.
En utilisant ![]() lorsque
lorsque ![]() ,
, ![]() .
.
4. Tirages de boules pour avoir deux boules noires consécutives
Mines Ponts MP 2018
On considère un sac dans lequel on a mis des boules blanches et des boules noires. Il y a deux fois plus de boules noires que de boules blanches. Le tirage s’effectue au hasard et avec remise.
On note ![]() la variable aléatoire égale au nombre de tirages pour obtenir deux boules noires consécutives. On pose
la variable aléatoire égale au nombre de tirages pour obtenir deux boules noires consécutives. On pose ![]() pour tout
pour tout ![]() .
.
Question 1
Montrer que : ![]() avec
avec
Question 2.
Démontrer que l’on a bien défini la loi d’une variable aléatoire.
Question 3.
Déterminer la loi de ![]() .
.
Question 4.
Montrer que ![]() admet des moments de tout ordre. Calculer son espérance et sa variance.
admet des moments de tout ordre. Calculer son espérance et sa variance.
Corrigé de l’exercice :
Question 1 :
Il est évident que ![]() .
.
On note ![]() « on tire une boule noire au
« on tire une boule noire au ![]() -ème tirage » et
-ème tirage » et ![]() « on tire une boule blanche au
« on tire une boule blanche au ![]() -ème tirage ».
-ème tirage ».
La famille ![]() est un système complet d’événements de probabilités non nulles.
est un système complet d’événements de probabilités non nulles.
Par la formule des probabilités totales si ![]() ,
,
![]()
![]()
![]()
![]()
![]()
car il reste ![]() tirages pour obtenir les deux noires consécutives.
tirages pour obtenir les deux noires consécutives.
![]()
![]() car il reste
car il reste ![]() tirages pour obtenir les deux noires consécutives, les deux premiers tirages étant « inutiles ».
tirages pour obtenir les deux noires consécutives, les deux premiers tirages étant « inutiles ».
![]() Si
Si ![]() .
.
![]() et
et ![]() .
.
On a donc prouvé que :
![]() .
.
Question 2 :
Les événements ![]() étant deux à deux incompatibles, la série de terme général
étant deux à deux incompatibles, la série de terme général ![]() pour
pour ![]() est convergente. On note
est convergente. On note 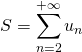 sa somme.
sa somme.
En sommant la relation ![]() ,
,
on obtient comme ![]() ,
,
![]()
et avec ![]()
![]() .
.
On a donc défini la loi d’une variable aléatoire car 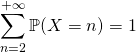 .
.
Question 3 :
L’équation caractéristique ![]() admet deux racines distinctes :
admet deux racines distinctes : ![]() et
et ![]() .
.
Il existe alors deux réels ![]() et
et ![]() tels que pour tout
tels que pour tout ![]() ,
, ![]()
(les puissances ![]() au lieu de puissances
au lieu de puissances ![]() simplifient les calculs qui suivent).
simplifient les calculs qui suivent).
En utilisant ![]() et
et ![]() , on obtient le système :
, on obtient le système : ![]()
![]()
![]()
![]()
![]()
donc pour tout ![]()
![]() .
.
Question 4 :
Pour tout ![]() la série de terme général
la série de terme général ![]() converge absolument car les rayons de convergence des séries
converge absolument car les rayons de convergence des séries ![]() et
et ![]() sont respectivement égaux à
sont respectivement égaux à ![]() et 3.
et 3.
On utilise ensuite 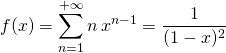 et
et 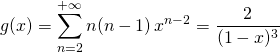 pour calculer l’espérance et la variance.
pour calculer l’espérance et la variance.
![]() Calcul de l’espérance :
Calcul de l’espérance :
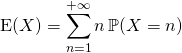
![]()
![]()
![]() .
.
![]() Calcul de la variance :
Calcul de la variance :
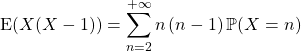
![]()
![]()
![]()
et enfin ![]()
![]() .
.
Pour compléter votre entraînement et vos révisions de mathématiques en Maths Spé, découvrez les autres cours en ligne de maths accessibles gratuitement :




