Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Les Matrices en Maths Spé
Résumé de cours Exercices et corrigés
Noyau, Image, Base Canonique de matrices en MP, PC, PSI, PT
1. Méthodes de calcul de  où
où  .
.
![]() M1. Par récurrence: on calcule
M1. Par récurrence: on calcule ![]() ,
, ![]() , … , etc, jusqu’à conjecturer une formule que l’on démontre par récurrence.
, … , etc, jusqu’à conjecturer une formule que l’on démontre par récurrence.
Par exemple,
![]() Si
Si ![]() , montrer par récurrence que
, montrer par récurrence que ![]() ,
, ![]() .
.
![]() Si
Si ![]() , montrer par récurrence que
, montrer par récurrence que ![]() ,
, ![]() et
et ![]()
![]() M2.Utilisation d’un polynôme
M2.Utilisation d’un polynôme ![]() annulateur de
annulateur de ![]()
(de préférence choisir ![]() non nul de degré
non nul de degré ![]() le plus faible possible tel que
le plus faible possible tel que ![]() ).
).
![]() Le chapitre « réduction des endomorphismes » donne une méthode pour trouver un polynôme annulateur de
Le chapitre « réduction des endomorphismes » donne une méthode pour trouver un polynôme annulateur de ![]()
Quand c’est possible, on choisira le polynôme minimal de ![]() (
(![]() ).
).
Le théorème de division euclidienne donne l’existence de (![]() tel que
tel que
![]()
On détermine ![]() en utilisant les racines de
en utilisant les racines de ![]() (voir ci-dessous).
(voir ci-dessous).
Il restera à calculer ![]() et à écrire que
et à écrire que ![]() , donc
, donc ![]()
![]() Cette méthode s’applique en particulier lorsque
Cette méthode s’applique en particulier lorsque ![]() , on pose
, on pose ![]() .
.
![]() Lorsque
Lorsque ![]() a
a ![]() racines distinctes
racines distinctes ![]() , on obtient un système de
, on obtient un système de ![]() équations à
équations à ![]() inconnues en écrivant que
inconnues en écrivant que
![]()
![]()
C’est un système qui permet de déterminer les ![]() coefficients du polynôme
coefficients du polynôme ![]() .
.
![]() Lorsque
Lorsque ![]() a une racine multiple, par exemple si
a une racine multiple, par exemple si ![]() avec
avec ![]() on écrit que
on écrit que ![]() est divisible par
est divisible par ![]()
![]()
Puis on écrit que les racines de ![]() sont racines de
sont racines de ![]()
![]() M3. Utilisation du binôme de Newton.
M3. Utilisation du binôme de Newton.
Si l’on peut écrire ![]() avec
avec ![]() , pour
, pour ![]()
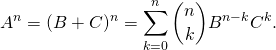
Cette méthode est intéressante
![]() lorsque
lorsque ![]() est une matrice scalaire et
est une matrice scalaire et ![]() une matrice triangulaire dont les éléments de la diagonale sont nuls (car alors
une matrice triangulaire dont les éléments de la diagonale sont nuls (car alors ![]() )
)
![]() ou lorsque
ou lorsque ![]() est la matrice formée uniquement de 1 (dans ce cas, l’expression
est la matrice formée uniquement de 1 (dans ce cas, l’expression ![]()
![]() suppose
suppose ![]() . Il faudra, dans les calculs, mettre à part le terme pour
. Il faudra, dans les calculs, mettre à part le terme pour ![]() ).
).
![]() M4. Si l’on peut trouver une matrice
M4. Si l’on peut trouver une matrice ![]() diagonale et une matrice inversible
diagonale et une matrice inversible ![]() telles que
telles que ![]() ,
, ![]() .
.
On rappelle que si ![]() ,
, ![]() .
.
![]() M5. Si l’on peut trouver une matrice
M5. Si l’on peut trouver une matrice ![]() triangulaire et une matrice inversible
triangulaire et une matrice inversible ![]() telles que
telles que ![]() ,
, ![]() .
.
On calcule ![]() en utilisant M1 ou M3.
en utilisant M1 ou M3.
L’utilisation de M2 ou M3 est plus simple que celle de M4 ou M5 car elle évite le calcul de ![]() .
.
UN PROF DE MATHS POUR EXCELLER
La pratique et la compréhension
clés de la réussite
Cours de maths en ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
2. Méthodes de calcul de l’inverse de  où
où 
![]() M1. Si
M1. Si ![]() où
où ![]() ,
, ![]() est inversible et
est inversible et ![]() .
.
En effet, en notant ![]() , on calcule
, on calcule
![]()
![]() .
.
![]() , donc la matrice
, donc la matrice ![]() est inversible d’inverse
est inversible d’inverse ![]() .
.
![]() M2. En utilisant un polynôme annulateur
M2. En utilisant un polynôme annulateur
Si l’on connaît ![]() tel que
tel que ![]() et
et ![]()
(donc ![]() ), en écrivant que
), en écrivant que
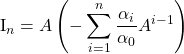
![]() est inversible et
est inversible et 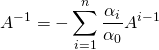
ou ![]()
Attention à ne pas oublier après ![]() la matrice
la matrice ![]() quand on n’utilise pas la notation
quand on n’utilise pas la notation ![]() !
!
![]() M3. Si
M3. Si ![]() est triangulaire,
est triangulaire, ![]() est inversible si, et seulement si, le produit des termes de la diagonale est non nul.
est inversible si, et seulement si, le produit des termes de la diagonale est non nul.
Dans ce cas, on considère que ![]() est la matrice de passage de la base
est la matrice de passage de la base ![]() à la base
à la base ![]()
Pour trouver ![]() , il suffit d’exprimer pour tout
, il suffit d’exprimer pour tout ![]() de
de ![]() , le vecteur
, le vecteur ![]() dans la base
dans la base ![]() .
.
La ![]() -ième colonne de
-ième colonne de ![]() est formée des coordonnées de
est formée des coordonnées de ![]() dans la base
dans la base ![]() .
.
![]() M4. Si
M4. Si ![]() est quelconque, on introduit une base
est quelconque, on introduit une base ![]() de
de ![]() et on note
et on note ![]() le vecteur de
le vecteur de ![]() dont les coordonnées par rapport à la base
dont les coordonnées par rapport à la base ![]() forment la
forment la ![]() -ème colonne de
-ème colonne de ![]()
Si l’on peut, pour tout ![]() , exprimer
, exprimer ![]() en fonction de
en fonction de ![]() , cela permet de démontrer que
, cela permet de démontrer que ![]() est un système générateur de
est un système générateur de ![]() donc une base de
donc une base de ![]()
Alors ![]() est la matrice de passage de la base
est la matrice de passage de la base ![]() à la base
à la base ![]() et
et ![]() est la matrice de passage de la base
est la matrice de passage de la base
![]() à la base
à la base ![]() .
.
La ![]() -ième colonne de
-ième colonne de ![]() est formée des coordonnées de
est formée des coordonnées de ![]() dans la base
dans la base ![]()
![]() M5. On peut aussi introduire
M5. On peut aussi introduire ![]() et
et ![]() et résoudre le système
et résoudre le système
![]() (c’est-à-dire calculer
(c’est-à-dire calculer ![]() en fonction de
en fonction de ![]() ) ce qui permet d’écrire
) ce qui permet d’écrire ![]()
![]() M6. On peut aussi utiliser la méthode du pivot de Gauss (mais c’est souvent une méthode compliquée).
M6. On peut aussi utiliser la méthode du pivot de Gauss (mais c’est souvent une méthode compliquée).
Dans une même matrice ![]() , on place la matrice
, on place la matrice ![]() à inverser suivie à droite de la matrice
à inverser suivie à droite de la matrice ![]() .
.
Par opérations élémentaires sur les lignes de la matrice ![]() , on doit arriver à transformer la matrice
, on doit arriver à transformer la matrice ![]() en une matrice contenant la matrice
en une matrice contenant la matrice ![]() suivie d’une matrice
suivie d’une matrice ![]() . Cette matrice
. Cette matrice ![]() est la matrice inverse de
est la matrice inverse de ![]() .
.
La méthode comporte trois étapes:
![]() Première étape : on obtient une matrice triangulaire sur les
Première étape : on obtient une matrice triangulaire sur les ![]() premières colonnes, de termes diagonaux non nuls (si l’un des ces termes est nul,
premières colonnes, de termes diagonaux non nuls (si l’un des ces termes est nul, ![]() n’est pas inversible et on arrête).
n’est pas inversible et on arrête).
![]() Deuxième étape : on obtient tous les termes de la diagonale égaux à 1.
Deuxième étape : on obtient tous les termes de la diagonale égaux à 1.
![]() Troisième étape : on obtient des zéros au dessus de la diagonale dans les
Troisième étape : on obtient des zéros au dessus de la diagonale dans les ![]() premières colonnes.
premières colonnes.
Attention ! toutes les opérations doivent être effectuées sur les lignes de la matrice.
![]() M7. On peut trouver l’inverse d’une matrice d’ordre 2 par utilisation de déterminants.
M7. On peut trouver l’inverse d’une matrice d’ordre 2 par utilisation de déterminants.
![]() est inversible
est inversible
![]()
![]()
et dans ce cas,
![]() .
.
Certains cours, au vu de leur complexité méritent d’être revus à plusieurs reprises et de manière très sérieuse même après le cours en prépa. Les cours en ligne de Maths en MP, les cours en ligne de Maths en PC et les cours en ligne de Maths en PT, ainsi que les cours en ligne de Maths en PSI sont de très bons supports supplémentaires en plus d’un professeur particulier de maths qui vous permettent d’améliorer votre compréhension des cours de Maths en Maths Spé.
3. Noyau et Image de  défini par sa matrice
défini par sa matrice
![]() M1. Détermination simultanée de l’image et du noyau
M1. Détermination simultanée de l’image et du noyau
Si ![]() a pour matrice
a pour matrice ![]() dans les bases
dans les bases ![]() et
et ![]() de
de ![]() et
et ![]() , on détermine le rang de la famille
, on détermine le rang de la famille ![]() en l’échelonnant (on raisonne par opérations élémentaires sur les colonnes de la matrice
en l’échelonnant (on raisonne par opérations élémentaires sur les colonnes de la matrice ![]() ) et en gardant soigneusement les opérations effectuées.
) et en gardant soigneusement les opérations effectuées.
On suppose que l’on arrive à :
![]()
![]()
![]()
où la famille ![]() est libre.
est libre.
Par cette méthode, on obtient:
![]() la matrice
la matrice ![]() est de rang
est de rang ![]() .
.
![]() les vecteurs
les vecteurs ![]() forment une base de
forment une base de ![]()
![]() les vecteurs
les vecteurs ![]() sont des vecteurs de
sont des vecteurs de ![]() . Après avoir vérifié qu’ils forment une famille libre, on peut affirmer qu’ils forment une base de
. Après avoir vérifié qu’ils forment une famille libre, on peut affirmer qu’ils forment une base de ![]() (c’est sous-espace vectoriel de
(c’est sous-espace vectoriel de ![]() de dimension égale à
de dimension égale à ![]() soit à
soit à ![]() ).
).
![]() M2. Détermination du noyau (et seulement du noyau)
M2. Détermination du noyau (et seulement du noyau)
Soit ![]() , dont la matrice dans les bases
, dont la matrice dans les bases ![]() de
de ![]() et
et ![]() de
de ![]() est notée
est notée ![]()
La méthode la plus simple est d’écrire que ![]()
c’est-à-dire d’introduire la matrice ![]() des coordonnées de
des coordonnées de ![]() dans la base
dans la base ![]() et de résoudre le système de
et de résoudre le système de ![]() équations à
équations à ![]() inconnues
inconnues ![]() obtenu en écrivant
obtenu en écrivant ![]() .
.
Penser à cette méthode, quand il s’agit de déterminer, pour ![]() et
et ![]() ,
, ![]() donc de trouver les
donc de trouver les ![]() tels que
tels que ![]() , ce qui s’écrit matriciellement sous la forme
, ce qui s’écrit matriciellement sous la forme ![]()
![]() M3. Détermination de l’image (et seulement de l’image)
M3. Détermination de l’image (et seulement de l’image)
On cherche une matrice ![]() équivalente à la matrice
équivalente à la matrice ![]() en échelonnant les colonnes de
en échelonnant les colonnes de ![]() par la méthode du pivot de Gauss. Les matrices
par la méthode du pivot de Gauss. Les matrices ![]() et
et ![]() ont même image.
ont même image.
Une base de Im ![]() est formée par les colonnes échelonnées à pivot non nul de la matrice
est formée par les colonnes échelonnées à pivot non nul de la matrice ![]()
COURS DE MATHS
Nous avons recruté pour vous les meilleurs professeurs particuliers de maths
S'EXERCER ET APPRENDRE
Avis Google France ★★★★★ 4,8 sur 5
4. Utilisation de la base canonique
Rappel : La base canonique de ![]() est formée par les matrices
est formée par les matrices
![]() où
où ![]()
(soit ![]() est la matrice carrée d’ordre
est la matrice carrée d’ordre ![]() dont tous les éléments sont nuls sauf celui à l’intersection de la ligne
dont tous les éléments sont nuls sauf celui à l’intersection de la ligne ![]() et de la colonne
et de la colonne
![]() qui est égal à 1).
qui est égal à 1).
![]()
Si ![]() ,
,
![]()
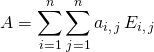 ,
,
![]()
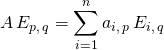
![]() et
et 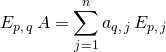 .
.
On peut utiliser la base canonique pour déterminer l’ensemble des matrices ![]() telles que pour tout
telles que pour tout ![]() de
de ![]() le couple
le couple ![]() vérifie une propriété donnée.
vérifie une propriété donnée.
Commencer par trouver les conditions nécessaires vérifiées par ![]() en appliquant l’hypothèse avec
en appliquant l’hypothèse avec ![]() .
.
5. Comment démontrer qu’une famille est génératrice de  ?
?
Pour démontrer que ![]() est une famille génératrice de
est une famille génératrice de ![]() ,
,
![]() M1. Montrer que
M1. Montrer que
![]() Vect
Vect![]()
![]() M2. Montrer que pour tout
M2. Montrer que pour tout ![]() de
de ![]() , on peut trouver des scalaires
, on peut trouver des scalaires ![]() tels que
tels que
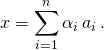
![]() M3. Si l’on connaît une base
M3. Si l’on connaît une base ![]() de
de ![]() , montrer que, pour tout
, montrer que, pour tout ![]() , on peut trouver
, on peut trouver ![]() de
de ![]() tel que
tel que 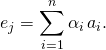 La famille
La famille ![]() engendre la base
engendre la base ![]() , c’est donc une famille génératrice de
, c’est donc une famille génératrice de ![]()
![]() M4. Pour démontrer que la famille infinie
M4. Pour démontrer que la famille infinie ![]() est génératrice de
est génératrice de ![]() , pour tout
, pour tout ![]() de
de ![]() , on démontre qu’il existe une famille presque nulle de scalaires
, on démontre qu’il existe une famille presque nulle de scalaires ![]() telle que
telle que ![]()
Beaucoup d’étudiants en prépa font le choix de prendre des cours particuliers ou de suivre des stages intensifs en maths spé de révisons, ce qui est très efficace pour améliorer ou garder un bon niveau. Mais entre 2 stages ou 2 cours particuliers les étudiants doivent continuer à s’entraîner, par exemple, sur les chapitres de maths suivants :
- les espaces vectoriels normés
- les suites et séries de fonctions
- l’intégration sur un intervalle quelconque
- les séries entières
- le dénombrement
Si vous souhaitez accéder à l’ensemble des méthodes et aux corrigés des exemples, n’hésitez pas à télécharger l’application PrepApp

