Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Réduction des endomorphismes en Maths Spé
Résumé de cours Exercices et corrigés
Résumé de cours et méthodes – Réduction en MP, PC, PSI et PT
1. Utilisation des polynômes d’endomorphismes ou de matrices
1.1. Polynôme minimal d’un endomorphisme
![]() est un
est un ![]() -espace vectoriel,
-espace vectoriel, ![]()
![]()
![]() ,
, ![]() est un morphisme d’algèbre.
est un morphisme d’algèbre.
![]() Ker
Ker ![]() est un idéal de
est un idéal de ![]() , appelé idéal annulateur de
, appelé idéal annulateur de ![]() .
.
![]() Im
Im ![]() est le sous-espace vectoriel engendré par
est le sous-espace vectoriel engendré par ![]() . On le note
. On le note ![]() .
.
Si ![]() est de dimension finie
est de dimension finie ![]() ,
,
![]() l’idéal annulateur de
l’idéal annulateur de ![]() est différent de
est différent de ![]() , il est engendré par un unique polynôme unitaire appelé polynôme minimal de
, il est engendré par un unique polynôme unitaire appelé polynôme minimal de ![]() et noté
et noté ![]() .
.
![]() Si
Si ![]() est le degré du polynôme minimal de
est le degré du polynôme minimal de ![]() ,
, ![]() admet pour base
admet pour base ![]() .
.
![]() Si
Si ![]() est un sev de
est un sev de ![]() non égal à
non égal à ![]() et
et ![]() -stable et si
-stable et si ![]() l’endomorphisme de
l’endomorphisme de ![]() induit par
induit par ![]() ,
, ![]() divise
divise ![]() .
.
1.2. Polynôme minimal d’une matrice
Soit ![]() .
.
![]()
![]() ,
, ![]() est un morphisme d’algèbres.
est un morphisme d’algèbres.
![]() Ker
Ker ![]() est un idéal de
est un idéal de ![]() , appelé idéal annulateur de
, appelé idéal annulateur de ![]() . Il est différent de
. Il est différent de ![]() , il est engendré par un unique polynôme unitaire appelé polynôme minimal de
, il est engendré par un unique polynôme unitaire appelé polynôme minimal de ![]() et noté
et noté ![]() .
.
![]() Im
Im ![]() est le sous-espace vectoriel engendré par
est le sous-espace vectoriel engendré par ![]() . On le note
. On le note ![]() .
.
![]() Si
Si ![]() est le degré du polynôme minimal de
est le degré du polynôme minimal de ![]() ,
, ![]() admet pour base
admet pour base ![]() .
.
![]() Si
Si ![]() est un endomorphisme de
est un endomorphisme de ![]() de matrice
de matrice ![]() dans une base de
dans une base de ![]() ,
, ![]() et
et ![]() ont même polynôme minimal.
ont même polynôme minimal.
1.3. Lemme de décomposition des noyaux
Si ![]() est un endomorphisme du
est un endomorphisme du ![]() -espace vectoriel
-espace vectoriel ![]() , si
, si ![]() sont des éléments de
sont des éléments de ![]() deux à deux premiers entre eux, de produit égal à
deux à deux premiers entre eux, de produit égal à ![]() ,
,
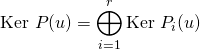 .
.
COURS DE MATHS A DOMICILE
Les meilleurs profs de maths pour
réussir sa scolarité
En ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
2. Synthèse des résultats – reduction des endomorphismes methodes
2.1. Pour un endomorphisme
Dans tout ce §, ![]() est un
est un ![]() -espace vectoriel de dimension finie
-espace vectoriel de dimension finie ![]() ,
,
![]() est un élément de
est un élément de ![]() ,
,
![]() un élément de
un élément de ![]() .
.
On note ![]() le polynôme caractéristique de
le polynôme caractéristique de ![]() .
.
2.1.1. Valeurs propres d’un endomorphisme
![]() Les conditions nécessaires et suffisantes :
Les conditions nécessaires et suffisantes :
![]()
![]()
![]() n’est pas injectif.
n’est pas injectif.
![]() ,
, ![]()
![]()
![]() La condition nécessaire:
La condition nécessaire:
Soit ![]() un élément de
un élément de ![]() .
.
Si ![]() valeur propre de
valeur propre de ![]() et
et ![]() , alors
, alors ![]() .
.
![]()
2.1.2. Polynôme caractéristique
![]()
![]() ,
, ![]() .
.
![]()
![]()
![]()
![]() les racines de
les racines de ![]() sont les valeurs propres de
sont les valeurs propres de ![]() .
.
![]() si
si ![]() est scindé sur
est scindé sur ![]() et
et ![]() , si
, si ![]() est l’ordre de multiplicité de
est l’ordre de multiplicité de ![]() si
si ![]()
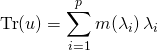 ,
, 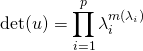 .
.
![]() Si
Si ![]() est un sev de
est un sev de ![]() non égal à
non égal à ![]() et
et ![]() -stable et si
-stable et si ![]() l’endomorphisme de
l’endomorphisme de ![]() induit par
induit par ![]() ,
, ![]() divise
divise
![]() .
.
![]() Théorème de Cayley-Hamilton :
Théorème de Cayley-Hamilton : ![]() .
.
2.1.3. Conditions de diagonalisibilité
![]() Les conditions nécessaires et suffisantes :
Les conditions nécessaires et suffisantes :
![]() est diagonalisable
est diagonalisable
![]() il existe une base de
il existe une base de ![]() formée de vecteurs propres de
formée de vecteurs propres de ![]()
![]() il existe une base de
il existe une base de ![]() dans laquelle la matrice de
dans laquelle la matrice de ![]() est diagonale
est diagonale
![]()
![]()
![]()
![]() est scindé dans
est scindé dans ![]() et pour tout
et pour tout ![]()
![]()
(![]() ordre de multiplicité de la valeur propre
ordre de multiplicité de la valeur propre ![]() dans
dans ![]() )
)
![]() il existe un polynôme
il existe un polynôme ![]() de
de ![]() scindé dans
scindé dans ![]() , à racines simples, tel que
, à racines simples, tel que ![]()
![]() lorsque
lorsque ![]() ,
, ![]() est un polynôme annulateur de
est un polynôme annulateur de ![]() . C’est alors le polynôme minimal de
. C’est alors le polynôme minimal de ![]() .
.
![]() le polynôme minimal de
le polynôme minimal de ![]() est scindé sur
est scindé sur ![]() à racines simples.
à racines simples.
![]() la matrice
la matrice ![]() de
de ![]() dans une base
dans une base ![]() est diagonalisable.
est diagonalisable.
![]()
![]() .
.
![]() La condition suffisante :
La condition suffisante :
Si ![]() = dim
= dim ![]() et si
et si ![]() a
a ![]() racines distinctes,
racines distinctes, ![]() est diagonalisable.
est diagonalisable.
2.1.4. Endomorphisme induit
Si ![]() est un sous-espace vectoriel de
est un sous-espace vectoriel de ![]() différent de
différent de ![]() stable pour l’endomorphisme
stable pour l’endomorphisme ![]() de
de ![]() , on note
, on note ![]() l’endomorphisme induit par
l’endomorphisme induit par ![]() sur
sur ![]() ,
,
![]() Le polynôme caractéristique de
Le polynôme caractéristique de ![]() divise le polynôme caractéristique de
divise le polynôme caractéristique de ![]()
![]() Si
Si ![]() est diagonalisable,
est diagonalisable, ![]() est diagonalisable.
est diagonalisable.
2.2. Pour une matrice
Dans tout ce ![]() ,
, ![]() et
et ![]() un élément de
un élément de ![]() .
.
On note ![]() le polynôme caractéris- tique de
le polynôme caractéris- tique de ![]() .
.
2.2.1. Valeurs propres d’une matrice
Les conditions nécessaires et suffisantes :
![]()
![]() est valeur propre de l’endomor- phisme canoniquement associé à
est valeur propre de l’endomor- phisme canoniquement associé à ![]()
![]() tel que
tel que ![]()
![]() n’est pas inversible
n’est pas inversible
![]()
![]()
![]() .
.
La condition nécessaire :
Soit ![]() un élément de
un élément de ![]() .
.
Si ![]() valeur propre de
valeur propre de ![]() et
et ![]() , alors
, alors ![]() .
.
Donc si ![]() ,
, ![]()
2.2.2. Polynôme caractéristique
![]()
![]()
![]() .
.
![]()
![]()
![]()
![]() les racines de
les racines de ![]() sont les valeurs propres de
sont les valeurs propres de ![]() .
.
![]() si
si ![]() est scindé sur
est scindé sur ![]() et
et ![]() si
si ![]() est l’ordre de multiplicité de
est l’ordre de multiplicité de ![]() pour
pour ![]() ,
,
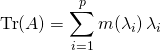 ,
, 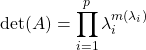
![]()
![]() ,
, ![]() et toute matrice
et toute matrice ![]() semblable à
semblable à ![]() ont même polynôme caractéristique.
ont même polynôme caractéristique.
![]() Théorème de Cayley-Hamilton :
Théorème de Cayley-Hamilton : ![]() .
.
2.2.3. Conditions de diagonalisibilité
Les conditions nécessaires et suffisantes :
![]() est diagonalisable
est diagonalisable
![]() l’endomorphisme canoniquement associé à
l’endomorphisme canoniquement associé à ![]() est diagonalisable.
est diagonalisable.
![]() il existe
il existe ![]() diagonale et
diagonale et ![]() telles que
telles que ![]()
![]()
![]()
![]() est scindé sur
est scindé sur ![]() et pour tout
et pour tout ![]() ,
, ![]()
(![]() ordre de multiplicité de la valeur propre
ordre de multiplicité de la valeur propre ![]() dans
dans ![]() )
)
![]() il existe un polynôme
il existe un polynôme ![]() de
de ![]() scindé sur
scindé sur ![]() , à racines simples, tel que
, à racines simples, tel que ![]()
![]() lorsque
lorsque ![]() ,
, ![]() est un polynôme annulateur de
est un polynôme annulateur de ![]() .
.
![]() le polynôme minimal de
le polynôme minimal de ![]() est scindé sur
est scindé sur ![]() à racines simples.
à racines simples.
![]()
![]() est la matrice d’un endomorphisme diagonalisable.
est la matrice d’un endomorphisme diagonalisable.
![]()
![]() .
.
La condition suffisante :
Si ![]() est carrée d’ordre
est carrée d’ordre ![]() et si
et si ![]() a
a ![]() racines distinctes, la matrice
racines distinctes, la matrice ![]() est diagonalisable.
est diagonalisable.
2.2.4. Cas particulier des matrices symétriques réelles (voir le chapitre espaces vectoriels euclidiens)
Théorème : Soit ![]() une matrice symétrique réelle carrée d’ordre
une matrice symétrique réelle carrée d’ordre ![]() .
.
![]() Le polynôme caractéristique de
Le polynôme caractéristique de ![]() est scindé sur
est scindé sur ![]()
![]() Les sous-espaces propres associés à des valeurs propres distinctes sont orthogonaux dans
Les sous-espaces propres associés à des valeurs propres distinctes sont orthogonaux dans ![]() , muni du produit scalaire canonique.
, muni du produit scalaire canonique.
![]()
![]() est diagonalisable et il existe
est diagonalisable et il existe ![]() orthogonale et
orthogonale et ![]() diagonale telles que
diagonale telles que ![]() .
.
Retrouvez l’ensemble des chapitres de Maths au programme de Maths Spé, grâce à nos cours en ligne pour les différentes filières. Ainsi, il vous est possible d’enrichir vos révisions et vos connaissances à l’aide d’une recherche de prof de maths à domicile, des cours en ligne de Maths en PC, des cours en ligne de Maths en MP et bien sûr des cours en ligne de Maths en PT et des cours en ligne de Maths en PSI.
3. Trouver le polynôme minimal de  ou de
ou de 
![]() 1er cas : le polynôme caractéristique de
1er cas : le polynôme caractéristique de ![]() (ou de
(ou de ![]() ) est scindé sur
) est scindé sur ![]() et
et ![]() étant deux à deux distincts,
étant deux à deux distincts,
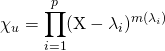 .
.
![]() Si
Si ![]() est diagonalisable,
est diagonalisable, 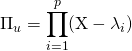 .
.
![]() Si
Si ![]() n’est pas diagonalisable, on cherche
n’est pas diagonalisable, on cherche ![]() sous la forme
sous la forme
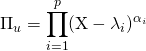
où ![]() ,
, ![]() , l’un au moins des
, l’un au moins des ![]() étant supérieur ou égal à 2.
étant supérieur ou égal à 2.
![]() 2ème cas :
2ème cas : ![]() et le polynôme caractéristique de
et le polynôme caractéristique de ![]() (ou de
(ou de ![]() ) n’est pas scindé sur
) n’est pas scindé sur ![]() .
.
On suppose que 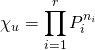 , les polynômes
, les polynômes ![]() étant deux à deux distincts unitaires, soit de degré 1, soit de degré 2 à discriminant strictement négatif et
étant deux à deux distincts unitaires, soit de degré 1, soit de degré 2 à discriminant strictement négatif et ![]() pour tout
pour tout ![]() .
.
Chercher le polynôme minimal sous la forme 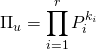
![]() où
où ![]() ,
, ![]() .
.
![]() M3. Détermination de l’image (et seulement de l’image)
M3. Détermination de l’image (et seulement de l’image)
On cherche une matrice ![]() équivalente à la matrice
équivalente à la matrice ![]() en échelonnant les colonnes de
en échelonnant les colonnes de ![]() par la méthode du pivot de Gauss. Les matrices
par la méthode du pivot de Gauss. Les matrices ![]() et
et ![]() ont même image.
ont même image.
Une base de Im ![]() est formée par les colonnes échelonnées à pivot non nul de la matrice
est formée par les colonnes échelonnées à pivot non nul de la matrice ![]()
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
4. Comment trouver les valeurs propres d’une matrice  ?
?
Remarque : les méthodes ci-dessous peuvent être appliquées à un endomorphisme ![]() en introduisant sa matrice
en introduisant sa matrice ![]() dans une base
dans une base ![]() de
de ![]() .
.
Des résultats importants :
![]() R1 : Si
R1 : Si ![]() est un
est un ![]() -espace vectoriel de dimension finie
-espace vectoriel de dimension finie ![]() , tout endomorphisme
, tout endomorphisme ![]() de
de ![]() admet au moins une valeur propre complexe car
admet au moins une valeur propre complexe car ![]() admet au moins une racine dans
admet au moins une racine dans ![]() .
.
Le résultat n’est pas vrai si ![]() est un
est un ![]() -espace vectoriel :
-espace vectoriel :
Prendre ![]() tel que
tel que ![]() et
et ![]() où
où ![]() ) est la base canonique de
) est la base canonique de
![]() ,
, ![]() .
.
![]() R2 : Si
R2 : Si ![]() ,
, ![]() admet au moins une valeur propre complexe.
admet au moins une valeur propre complexe.
![]() R3 : Si
R3 : Si ![]() et si
et si ![]() est impair,
est impair, ![]() admet au moins une valeur propre réelle (puisque
admet au moins une valeur propre réelle (puisque
![]() et
et ![]() est impair).
est impair).
![]() R4 : Si
R4 : Si ![]() , les valeurs propres non réelles de
, les valeurs propres non réelles de ![]() considérée comme élément de
considérée comme élément de
![]() sont deux à deux conjuguées et les sous-espaces propres de valeurs propres conjuguées ont même dimension.
sont deux à deux conjuguées et les sous-espaces propres de valeurs propres conjuguées ont même dimension.
Quand on écrit ![]()
les scalaires ![]() sont deux à deux distincts.
sont deux à deux distincts.
Lorsque ![]() est scindé et les valeurs propres ne sont pas distinctes 2 à 2, il faut dire : on note
est scindé et les valeurs propres ne sont pas distinctes 2 à 2, il faut dire : on note ![]() une liste de valeurs propres de
une liste de valeurs propres de ![]() .
.
![]() M1. En calculant son polynôme caractéristique c’est-à-dire en calculant lorsque
M1. En calculant son polynôme caractéristique c’est-à-dire en calculant lorsque ![]() ,
, ![]()
Cette méthode a deux inconvénients :
![]() cela nécessite un calcul de déterminant (qui peut être pénible quand
cela nécessite un calcul de déterminant (qui peut être pénible quand ![]() ).
).
![]() puis cela nécessite la recherche des racines d’un polynôme de degré
puis cela nécessite la recherche des racines d’un polynôme de degré ![]() (les calculs pouvant être compliqués pour
(les calculs pouvant être compliqués pour ![]() lorsque le polynôme caractéristique n’a pas de racine évidente).
lorsque le polynôme caractéristique n’a pas de racine évidente).
Mais elle peut être intéressante :
si ![]() est facilement calculable et factorisable, on connaît alors les valeurs propres de
est facilement calculable et factorisable, on connaît alors les valeurs propres de ![]() .
.
Exercice : Polynôme caractéristique d’une matrice compagnon. 🧡
Soit ![]() et
et ![]() ,
,
 ,
, 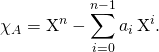
Montrer que ![]() est diagonalisable ssi le polynôme caractéristique de
est diagonalisable ssi le polynôme caractéristique de ![]() est scindé à racines simples.
est scindé à racines simples.
5. Comment trouver les éléments propres d’une matrice ?
![]() Rappel de deux résultats qui peuvent simplifier les calculs:
Rappel de deux résultats qui peuvent simplifier les calculs:
1) Si ![]() et si
et si ![]() ,
, ![]()
et ![]() .
.
Si ![]() est valeur propre simple de
est valeur propre simple de ![]() ,
, ![]() .
.
2) Si ![]() et si
et si ![]() est une valeur propre de
est une valeur propre de ![]() ,
,
![]()
![]() est valeur propre de
est valeur propre de ![]() de même ordre de multiplicité,
de même ordre de multiplicité,
![]()
![]() vérifie
vérifie
![]() .
.
Il suffit donc de déterminer ![]() .
.
![]() M1. On connaît déjà Sp
M1. On connaît déjà Sp![]()
(en utilisant une des méthodes du § II-) ou des conditions nécessaires sur les valeurs propres de ![]() :
:
il suffit de résoudre pour ces valeurs ![]() de
de ![]() , l’équation
, l’équation ![]() , où
, où ![]() .
.
![]() M2. On ne connaît pas Sp
M2. On ne connaît pas Sp![]() (et on ne veut pas calculer
(et on ne veut pas calculer ![]() ) :
) :
il faut chercher ![]() et
et ![]() et
et ![]() tels que
tels que ![]() .
.
Pour cela, on peut :
![]() utiliser le pivot de Gauss, chercher un système triangulaire équivalent et écrire que le système ainsi obtenu admet une solution non nulle (c’est à dire que la matrice
utiliser le pivot de Gauss, chercher un système triangulaire équivalent et écrire que le système ainsi obtenu admet une solution non nulle (c’est à dire que la matrice ![]() triangulaire du système ainsi obtenu est non inversible si, et seulement si,
triangulaire du système ainsi obtenu est non inversible si, et seulement si, ![]() si, et seulement si, le produit des termes de la diagonale de
si, et seulement si, le produit des termes de la diagonale de ![]() est nul).
est nul).
![]() par combinaison linéaire des
par combinaison linéaire des ![]() équations, obtenir une condition nécessaire portant sur
équations, obtenir une condition nécessaire portant sur ![]() ou sur les
ou sur les ![]() et étudier ensuite la réciproque.
et étudier ensuite la réciproque.
Il est indéniable que le travail personnel est la clé de la réussite en prépa et notamment en Maths Spé. Ainsi, pour vous aider à atteindre vos objectifs, nous vous mettons à disposition l’ensemble des chapitres des Maths au programme de Maths Spé, en voici quelques un :
- les matrices
- les espaces vectoriels normés
- les suites et séries de fonctions
- l’intégration sur un intervalle quelconque
- les séries entières
Si vous souhaitez accéder à l’ensemble des méthodes et aux corrigés des exemples, n’hésitez pas à télécharger l’application PrepApp

