Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Séries entières en Maths Spé
Résumé de cours Exercice et corrigés
Résumé de cours et méthodes – Séries entières
1. Trouver le rayon de convergence  de la série de terme général
de la série de terme général  ?
?
Il faut avoir en mémoire la représentation suivante, si ![]() a un rayon de convergence
a un rayon de convergence ![]() :
:
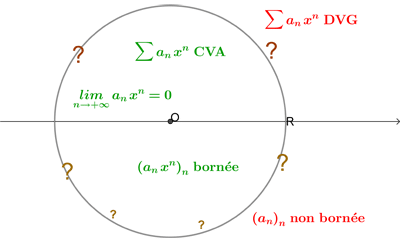
A la question : définition du rayon de convergence ![]() de
de ![]() la réponse attendue est :
la réponse attendue est :
![]() est la borne supérieure de l’ensemble
est la borne supérieure de l’ensemble ![]()
si cet ensemble est majoré et ![]() sinon.
sinon.
Le dessin précédent donne lorsque ![]() est fini et
est fini et ![]() :
:
![]() Si
Si ![]() ,
,
![]()
![]() converge absolument
converge absolument
![]()
![]()
![]() la suite
la suite ![]() est bornée.
est bornée.
![]() Si
Si ![]() ,
,
![]()
![]() diverge grossièrement
diverge grossièrement
![]() la suite
la suite ![]() ne converge pas vers
ne converge pas vers ![]()
![]() la suite
la suite ![]() n’est pas bornée.
n’est pas bornée.
![]() Si
Si ![]() ,
,
l’étude est à faire selon la valeur de la suite ![]() , on peut avoir :
, on peut avoir :
![]() convergence en tout
convergence en tout ![]()
(exemple ![]() )
)
![]() convergence en certains
convergence en certains ![]() et divergence en d’autres
et divergence en d’autres ![]()
(exemple ![]() )
)
![]() divergence pour tout
divergence pour tout ![]()
(exemple ![]() ).
).
![]() M1. Par double inégalité :
M1. Par double inégalité :
![]() S’il existe
S’il existe ![]() tel que la série de terme général
tel que la série de terme général ![]() converge :
converge : ![]() .
.
![]() S’il existe
S’il existe ![]() tel que la suite
tel que la suite ![]() soit bornée :
soit bornée : ![]() .
.
![]() S’il existe
S’il existe ![]() tel que la série de terme général
tel que la série de terme général ![]() diverge :
diverge : ![]() .
.
![]() S’il existe
S’il existe ![]() tel que la suite
tel que la suite ![]() ne soit pas bornée :
ne soit pas bornée : ![]() .
.
Tracer le disque de convergence et placer le point d’affixe ![]() dans le disque fermé de centre
dans le disque fermé de centre ![]() et de rayon
et de rayon ![]() et le point d’affixe
et le point d’affixe ![]() à l’extérieur du disque ouvert de convergence.
à l’extérieur du disque ouvert de convergence.
![]() M2. Par utilisation de la règle de d’Alembert
M2. Par utilisation de la règle de d’Alembert
M2.1. Il vaut mieux faire la démonstration complète à partir de la règle de d’Alembert pour les séries numériques :
On vérifie que ![]() , on démontre que le quotient
, on démontre que le quotient ![]() où
où ![]() admet une limite que l’on met en évidence.
admet une limite que l’on met en évidence.
![]() Si cette limite est nulle,
Si cette limite est nulle, ![]() converge pour tout
converge pour tout ![]() , donc
, donc ![]() .
.
![]() Si cette limite est égale à
Si cette limite est égale à ![]() avec
avec ![]() ,
, ![]() converge si
converge si ![]() et diverge si
et diverge si ![]() , donc
, donc ![]() .
.
M2.2. En utilisant la forme suivante à la limite du programme :
On vérifie que ![]() , on démontre que le quotient
, on démontre que le quotient ![]() admet une limite
admet une limite ![]() que l’on met en évidence.
que l’on met en évidence.
![]() Si
Si ![]() ,
, ![]() .
.
![]() Si
Si ![]() ,
, ![]() .
.
Important : la règle de d’Alembert ne peut servir qu’à déterminer un rayon de convergence, elle n’est d’aucune utilité lorsque l’on connaît le rayon de convergence de ![]() .
.
Ne pas oublier de préciser que ![]() en utilisant M2.1.
en utilisant M2.1.
Il est indispensable d’utiliser M2.1. pour les séries dites « lacunaires » (par exemple si les ![]() sont nuls ou si les
sont nuls ou si les ![]() sont nuls).
sont nuls).
La règle de d’Alembert est assez efficace lorsque ![]() est un produit de facteurs.
est un produit de facteurs.
Lorsque ![]() est « compliquée », il vaut mieux chercher avant un équivalent simple
est « compliquée », il vaut mieux chercher avant un équivalent simple ![]() de
de ![]() . On rappelle que
. On rappelle que ![]() et
et ![]() ont alors même rayon de convergence.
ont alors même rayon de convergence.
![]() M3. Par comparaison à une série de terme général
M3. Par comparaison à une série de terme général ![]() dont on connaît le rayon de convergence
dont on connaît le rayon de convergence ![]() :
:
![]() M3.1. si
M3.1. si ![]() ,
, ![]() :
: ![]()
![]() M3.2. si
M3.2. si ![]() :
: ![]()
![]() M3.3. si
M3.3. si ![]() :
: ![]() .
.
![]() M4- Par utilisation des opérations sur les séries entières :
M4- Par utilisation des opérations sur les séries entières :
![]() M4.1. Si
M4.1. Si ![]() et
et ![]() ont pour rayons de convergence respectifs
ont pour rayons de convergence respectifs ![]() et
et ![]() , le rayon de convergence
, le rayon de convergence ![]() de
de ![]() est égal à
est égal à ![]() lorsque
lorsque ![]() et supérieur ou égal à
et supérieur ou égal à ![]() lorsque
lorsque ![]() .
.
![]() M4.2. Si
M4.2. Si ![]() et
et ![]() ont pour rayons de convergence respectifs
ont pour rayons de convergence respectifs ![]() et
et ![]() , le rayon de convergence
, le rayon de convergence ![]() de la série produit de Cauchy,
de la série produit de Cauchy, ![]() où
où 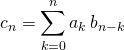 , est supérieur ou égal à
, est supérieur ou égal à ![]() .
.
![]() M4.3. Il y a conservation du rayon de convergence par dérivation ou intégration terme à terme.
M4.3. Il y a conservation du rayon de convergence par dérivation ou intégration terme à terme.
![]() M5. Si l’on connaît les rayons de convergence
M5. Si l’on connaît les rayons de convergence ![]() et
et ![]() de
de ![]() et de
et de ![]() , le rayon
, le rayon ![]() de convergence de
de convergence de ![]() est égal à
est égal à ![]()
2. Comment utiliser les propriétés de la somme d’une série entière de terme général  de rayon de convergence
de rayon de convergence  ?
?
![]() P1. La série de fonctions
P1. La série de fonctions ![]() est normalement convergente sur tout segment inclus dans l’intervalle ouvert de convergence
est normalement convergente sur tout segment inclus dans l’intervalle ouvert de convergence ![]() .
.
![]() P1B. La série de fonctions
P1B. La série de fonctions ![]() est normalement convergente sur tout compact inclus dans le disque ouvert de convergence
est normalement convergente sur tout compact inclus dans le disque ouvert de convergence ![]() .
.
![]() P2. La somme de la série est continue sur l’intervalle ouvert de convergence et sur le disque ouvert de convergence.
P2. La somme de la série est continue sur l’intervalle ouvert de convergence et sur le disque ouvert de convergence.
![]() P3. Si
P3. Si ![]() est le rayon de convergence de
est le rayon de convergence de ![]() et si
et si ![]() converge, la somme
converge, la somme ![]() est continue sur
est continue sur ![]() .
.
La démonstration est obligatoire.
![]() P4. La somme
P4. La somme ![]() de la série est de classe
de la série est de classe ![]() sur l’intervalle
sur l’intervalle ![]() et on obtient sa dérivée en dérivant terme à terme la somme de la série de terme général
et on obtient sa dérivée en dérivant terme à terme la somme de la série de terme général ![]() .
.
![]() P5. On peut calculer les dérivées successives en
P5. On peut calculer les dérivées successives en ![]() de la somme
de la somme ![]() de la série entière de terme général
de la série entière de terme général ![]() :
:
![]() .
.
![]() P6. On obtient une primitive de la somme
P6. On obtient une primitive de la somme ![]() de la série sur
de la série sur ![]() en intégrant terme à terme la série de terme général
en intégrant terme à terme la série de terme général ![]() .
.
![]() P7. On peut intervertir le signe
P7. On peut intervertir le signe ![]() et le signe
et le signe ![]() sur tout segment inclus dans l’intervalle ouvert de convergence
sur tout segment inclus dans l’intervalle ouvert de convergence
pour tout ![]() ,
, 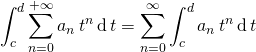
![]() P8. Unicité des coefficients du développement en série entière :
P8. Unicité des coefficients du développement en série entière :
s’il existe ![]() tel que
tel que ![Rendered by QuickLaTeX.com \displaystyle \forall x \in \; ]-\alpha , \alpha[, \; \sum _{n = 0} ^{+\infty} a_n \, x^n = \sum _{n = 0} ^{+\infty} b_n \, x^n](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-a85c1d35a95252d2d0e8749dc28a1294_l3.png) pour tout
pour tout ![]() de
de ![]() ,
, ![]() .
.
![]() P9. Pour démontrer qu’une fonction
P9. Pour démontrer qu’une fonction ![]() est de classe
est de classe ![]() au voisinage de
au voisinage de ![]() , il suffit de prouver que
, il suffit de prouver que ![]() est la somme d’une série entière sur
est la somme d’une série entière sur ![]() .
.
C’est utilisable en particulier pour ![]() ,
, ![]() ,
, ![]() ,
, ![]()
(avec démonstration et en prolongeant par continuité la fonction en 0).
![]() P10. On peut en déduire le développement limité à l’ordre
P10. On peut en déduire le développement limité à l’ordre ![]() au voisinage de
au voisinage de ![]() de
de ![]() :
:
si pour ![]() où
où ![]() ,
,  , alors
, alors 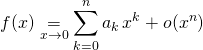 .
.
3. Comment démontrer qu’une fonction  est développable en série entière sur
est développable en série entière sur ![Rendered by QuickLaTeX.com ] - \alpha , \, \alpha[](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%2065%2018%22%3E%3C/svg%3E) ?
?
![]() M1. En utilisant la formule de Taylor :
M1. En utilisant la formule de Taylor :
![]() M1.1. Par la formule de Taylor avec reste intégral (peu utilisé).
M1.1. Par la formule de Taylor avec reste intégral (peu utilisé).
Par la condition nécessaire et suffisante : ![]() étant supposée de classe
étant supposée de classe ![]() sur
sur ![]() ,
, ![]() où
où 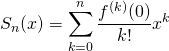 et
et ![]() .
.
![]() est développable en série entière sur
est développable en série entière sur ![]() ssi pour tout
ssi pour tout ![]() de
de ![]() , la suite de terme général
, la suite de terme général ![]() converge vers
converge vers ![]() .
.
![]() M1.2. Par la condition suffisante :
M1.2. Par la condition suffisante :
![]() étant supposée de classe
étant supposée de classe ![]() sur
sur ![]() ,
, ![]() est développable en série entière sur
est développable en série entière sur ![]() lorsque la suite de terme général
lorsque la suite de terme général ![]()
converge vers ![]() .
.
![]() M2. En utilisant des sommes de DSE connus. C’est utilisable :
M2. En utilisant des sommes de DSE connus. C’est utilisable :
![]() 1. pour tout polynôme en
1. pour tout polynôme en ![]() ou
ou ![]() , en linéarisant l’expression.
, en linéarisant l’expression.
![]() 2. pour toute expression de la forme
2. pour toute expression de la forme ![]() ou
ou ![]() , en introduisant
, en introduisant ![]() .
.
![]() 3. pour tout polynôme en
3. pour tout polynôme en ![]() et
et ![]() , en exprimant
, en exprimant ![]() et
et ![]() en fonction de
en fonction de ![]() et de
et de ![]() .
.
![]() 4. utiliser
4. utiliser ![]() et pour
et pour ![]() .
.
![]() 5. pour
5. pour ![]() , utiliser :
, utiliser : ![]()
pour ![]() , utiliser
, utiliser ![]() .
.
![]() M3. En intégrant des DSE connus (par exemple pour
M3. En intégrant des DSE connus (par exemple pour ![]() ,
, ![]() ,
, ![]() ).
).
![]() M4. En dérivant des DSE connus (pour retrouver par exemple le DSE sur
M4. En dérivant des DSE connus (pour retrouver par exemple le DSE sur ![]() de
de ![]() ).
).
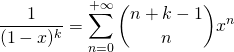 .
.
![]() M5. En utilisant des produits de DSE connus.
M5. En utilisant des produits de DSE connus.
Si ![]()
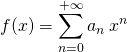 et si
et si 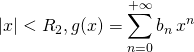 , en notant
, en notant ![]() , si
, si ![]()
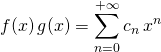 où pour tout
où pour tout  .
.
Prendre le temps d’écrire la formule avant de faire l’application numérique.
Si certaines difficultés persistent n’hésitez pas à bien relire votre cours ou prendre cours de maths à Lyon et à croiser les méthodes et les exemples de cours avec les notions de cours présentes dans les cours en ligne de Maths en PC, les cours en ligne de Maths en PSI ou encore les cours en ligne de Maths en MP et aussi les cours en ligne de PT en Maths.
![]() M6. En utilisant des fractions rationnelles dont le dénominateur ne s’annule pas :
M6. En utilisant des fractions rationnelles dont le dénominateur ne s’annule pas :
On développe ![]() en éléments simples dans le domaine complexe soit sous la forme de sommes de quantité du type suivant :
en éléments simples dans le domaine complexe soit sous la forme de sommes de quantité du type suivant :
![]() pour
pour ![]() , si
, si ![]() ,
,
![]()
![]() .
.
![]() pour
pour ![]() et
et ![]() si
si ![]()
![]()
![]() .
.
On peut conserver les termes de la forme ![]() où
où ![]() et
et ![]() , en utilisant les calculs précédents en remplaçant
, en utilisant les calculs précédents en remplaçant ![]() par
par ![]() .
.
![]() M7. Par utilisation d’équations différentielles :
M7. Par utilisation d’équations différentielles :
a) On démontre que ![]() est développable en série entière
est développable en série entière
b) On cherche une équation différentielle ![]() dont
dont ![]() est solution et on l’écrit de façon à ce que les calculs qui suivent soient simples.
est solution et on l’écrit de façon à ce que les calculs qui suivent soient simples.
c) On écrit qu’il existe ![]() tel que
tel que ![]() , puis que
, puis que ![]() est solution de
est solution de ![]() sur
sur ![]() .
.
En utilisant l’unicité du DSE, on obtient une relation entre les coefficients ![]() .
.
d) On calcule ![]() et le rayon de convergence.
et le rayon de convergence.
e) Si l’on obtient une seule suite ![]() , on a trouvé le développement en série entière de
, on a trouvé le développement en série entière de ![]() .
.
Si l’on obtient plusieurs suites ![]() , on cherche la suite qui convient en utilisant
, on cherche la suite qui convient en utilisant ![]() et éventuellement
et éventuellement ![]() .
.
variante : (c’est la méthode utilisée pour trouver le développement en série entière de ![]()
a) On ne sait pas démontrer que ![]() est développable en série entière mais on peut démontrer que
est développable en série entière mais on peut démontrer que ![]() est la seule solution d’une équation différentielle
est la seule solution d’une équation différentielle ![]() vérifiant de plus une condition
vérifiant de plus une condition ![]() .
.
b) On démontre qu’il existe une et une seule fonction ![]() développable en série entière sur
développable en série entière sur ![]() solution de
solution de ![]() et vérifiant la condition
et vérifiant la condition ![]() .
.
c) Alors ![]() sur
sur ![]() , donc
, donc ![]() est développable en série entière sur
est développable en série entière sur ![]() .
.
a) Avant de se lancer dans les calculs, voir s’il n’y a pas de simplification possible (par exemple, ![]() paire ou impaire).
paire ou impaire).
b) On remplace ![]() par son développement en série entière dans
par son développement en série entière dans ![]() . On développe les calculs.
. On développe les calculs.
On regroupe les termes en ![]() , ceux en
, ceux en ![]() , ceux en
, ceux en ![]() , etc … . On effectue des changements d’indice de façon à ce que toutes les sommes obtenues s’expriment en fonction de
, etc … . On effectue des changements d’indice de façon à ce que toutes les sommes obtenues s’expriment en fonction de ![]() .
.
les coefficients des ![]() doivent être indépendants de
doivent être indépendants de ![]() !
!
c) Si l’on obtient ![]() en fonction de
en fonction de ![]() il faut calculer séparément
il faut calculer séparément ![]() en fonction de
en fonction de ![]() ou
ou ![]() et
et ![]() en fonction de
en fonction de ![]() ou
ou ![]() .
.
COURS DE MATHS
Nous avons recruté pour vous les meilleurs professeurs particuliers de maths
S'EXERCER ET APPRENDRE
Avis Google France ★★★★★ 4,8 sur 5
4. Comment calculer la somme d’une série entière ?
![]() M1. cas où
M1. cas où ![]() où
où ![]() et
et ![]() .
.
En utilisant un équivalent de ![]() , démontrer que le rayon de convergence est égal à
, démontrer que le rayon de convergence est égal à ![]() .
.
Décomposer ![]() dans la base
dans la base ![]()
![]() ,
,
de façon à pouvoir utiliser les sommes de séries suivantes :
si ![]()

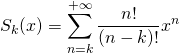
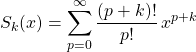
![]() .
.
![]() M2. cas où
M2. cas où ![]() où
où ![]() et
et ![]() .
.
En utilisant un équivalent de ![]() , démontrer que le rayon de convergence est égal à
, démontrer que le rayon de convergence est égal à ![]() .
.
Décomposer ![]() dans la base
dans la base ![]()
![]() ,
,
de façon à se ramener à des sommes de séries de la forme :
si ![]() ,
,
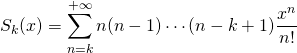
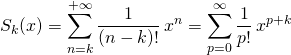
![]() .
.
![]() M3. cas où
M3. cas où ![]() où
où ![]() et
et ![]() sont des fonctions polynômes et
sont des fonctions polynômes et ![]() .
.
Décomposer la fraction ![]() en éléments simples.
en éléments simples.
On saura trouver la somme lorsque l’on obtient des termes de la forme :
a) ![]() où
où ![]() , en utilisant le changement d’indice
, en utilisant le changement d’indice ![]() , on se ramène à la somme
, on se ramène à la somme 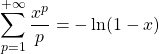 .
.
b)![]() , utiliser le changement de variable :
, utiliser le changement de variable : ![]() et
et ![]() , de façon à se ramener au calcul de
, de façon à se ramener au calcul de 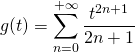 ou
ou 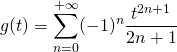 .
.
Dans ce cas, on calcule ![]() pour se ramener à la somme d’une série géométrique.
pour se ramener à la somme d’une série géométrique.
![]() M4. cas où
M4. cas où ![]() où
où ![]() et
et ![]() sont des fonctions polynômes et
sont des fonctions polynômes et ![]() .
.
Décomposer la fraction ![]() en éléments simples.
en éléments simples.
On saura trouver la somme lorsque l’on obtient des termes de la forme :
a) ![]() où
où ![]() , introduire
, introduire 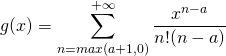 puis calculer
puis calculer ![]() .
.
b)![]() , utiliser le changement de variable :
, utiliser le changement de variable : ![]() et
et ![]() , de façon à introduire
, de façon à introduire 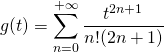
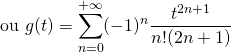
et calculer ![]() .
.
![]() M5. utilisation d’une équation différentielle : (uniquement si c’est suggéré).
M5. utilisation d’une équation différentielle : (uniquement si c’est suggéré).
a) Écrire que ![]() est solution d’une équation différentielle
est solution d’une équation différentielle ![]() .
.
si l’équation différentielle n’est pas donnée par l’énoncé, trouver une expression sans dénominateur liant ![]() et
et ![]() (et éventuellement
(et éventuellement ![]() ), sommer les relations ainsi obtenues multipliées par
), sommer les relations ainsi obtenues multipliées par ![]() (ou
(ou ![]() ) et exprimer ces sommes à l’aide de
) et exprimer ces sommes à l’aide de ![]() (éventuellement
(éventuellement ![]() ) et
) et ![]() .
.
b) Résoudre ![]() .
.
c) Parmi les solutions de ![]() , chercher celle qui convient (en général, on utilisera
, chercher celle qui convient (en général, on utilisera ![]() et même
et même ![]() .
.
5. Développement en série entière d’une intégrale à paramètre
Hypothèses soit à développer en série entière ![]() lorsque
lorsque ![]() ,
, ![]() et si pour tout
et si pour tout ![]() est développable en série entière.
est développable en série entière.
1- Montrer que l’on peut écrire pour tout ![Rendered by QuickLaTeX.com x \in \; ]- R , R[,\; f(x, t) = \displaystyle \sum_{n = 0} ^{+\infty} a_n(t) x^n](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-72524a6549f941fe86aef2a99fde3855_l3.png) pour
pour ![]() .
.
2- Fixer ![]() dans
dans ![]() . Lorsque
. Lorsque ![]() , poser
, poser ![]() (étape indispensable).
(étape indispensable).
Il est important de bien faire attention à la variable de la fonction ![]() il s’agit de la variable d’intégration.
il s’agit de la variable d’intégration.
3- Montrer que pour tout ![]() , la fonction
, la fonction ![]() est continue sur
est continue sur ![]() .
.
4- Montrer que la série de fonctions de terme général ![]() (de la variable
(de la variable ![]() ) converge uniformément sur
) converge uniformément sur ![]() .
.
On peut alors intervertir l’intégrale sur ![]() et le signe
et le signe ![]() et écrire que :
et écrire que :
![]()
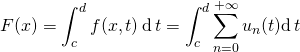
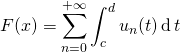
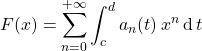
 .
.
Autre cas : lorsque l’intervalle d’intégration ![]() de bornes
de bornes ![]() et
et ![]() n’est pas un segment et lorsque pour tout
n’est pas un segment et lorsque pour tout ![]() est développable en série entière.
est développable en série entière.
1- Montrer que l’on peut écrire pour tout ![Rendered by QuickLaTeX.com x \in \; ]- R , R[,\; f(x, t) = \displaystyle \sum_{n = 0} ^{+\infty} a_n(t) x^n](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-72524a6549f941fe86aef2a99fde3855_l3.png) pour
pour ![]() .
.
2- Fixer ![]() dans
dans ![]() . Lorsque
. Lorsque ![]() , poser
, poser ![]() (étape indispensable).
(étape indispensable).
Il est important de bien faire attention à la variable de la fonction ![]() il s’agit de la variable d’intégration.
il s’agit de la variable d’intégration.
3- Montrer que pour tout ![]() , la fonction
, la fonction ![]() est continue et intégrable sur
est continue et intégrable sur ![]() .
.
4- Par hypothèse, la série de fonctions de terme général ![]() (de la variable
(de la variable ![]() ) converge simplement sur
) converge simplement sur ![]() et sa somme
et sa somme ![]() est continue sur
est continue sur ![]() .
.
5- Montrer que la série de terme général ![]() converge.
converge.
On peut alors utiliser le théorème d’intégration terme à terme et intervertir l’intégrale sur ![]() et le signe
et le signe ![]() et conclure comme dans le premier cas que :
et conclure comme dans le premier cas que :
![]()
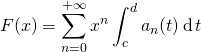
Autre cas : lorsque l’intervalle d’intégration ![]() de bornes
de bornes ![]() et
et ![]() n’est pas un segment et lorsque pour tout
n’est pas un segment et lorsque pour tout ![]() est développable en série entière.
est développable en série entière.
1- Montrer que l’on peut écrire pour tout ![Rendered by QuickLaTeX.com x \in \; ]- R , R[,\; f(x, t) = \displaystyle \sum_{n = 0} ^{+\infty} a_n(t) x^n](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-72524a6549f941fe86aef2a99fde3855_l3.png) pour
pour ![]() .
.
2- Fixer ![]() dans
dans ![]() . Lorsque
. Lorsque ![]() , poser
, poser ![]() (étape indispensable).
(étape indispensable).
Il est important de bien faire attention à la variable de la fonction ![]() il s’agit de la variable d’intégration.
il s’agit de la variable d’intégration.
3- Montrer que pour tout ![]() , la fonction
, la fonction ![]() est continue et intégrable sur
est continue et intégrable sur ![]() .
.
4- Par hypothèse, la série de fonctions de terme général ![]() (de la variable
(de la variable ![]() ) converge simplement sur
) converge simplement sur ![]() et sa somme
et sa somme ![]() est continue sur
est continue sur ![]() .
.
5- Montrer que la série de terme général ![]() converge.
converge.
On peut alors utiliser le théorème d’intégration terme à terme et intervertir l’intégrale sur ![]() et le signe
et le signe ![]() et conclure comme dans le premier cas que :
et conclure comme dans le premier cas que :
![]()
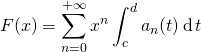 .
.
De nombreux autres cours en ligne ont également été rédigés par nos professeurs, pour accompagner les étudiants dans leur préparation aux concours post-prépa, en voici quelques-uns :
- le dénombrement
- les intégrales à paramètre
- les variables aléatoires
- les probabilités
- les espaces préhilbertiens
Si vous souhaitez accéder à l’ensemble des méthodes et aux corrigés des exemples, n’hésitez pas à télécharger l’application PrepApp

