Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Méthodes Suites et séries de fonctions en MP, PC, PSI
Résumé de cours Exercices et corrigés
Résumé de cours et méthodes – Suites et séries de fonctions
1. Comment démontrer qu’une suite de fonctions converge uniformément sur  ?
?
Les fonctions ![]() sont définies sur
sont définies sur ![]() à valeurs dans
à valeurs dans ![]() (resp. l’e.v.n.
(resp. l’e.v.n. ![]() ).
).
a) On détermine, pour tout ![]() de
de ![]() , la limite
, la limite ![]() de la suite de scalaires (resp. vecteurs)
de la suite de scalaires (resp. vecteurs) ![]() , c’est-à-dire on étudie la limite simple de
, c’est-à-dire on étudie la limite simple de ![]() .
.
b) On vérifie que les fonctions ![]() sont bornées sur
sont bornées sur ![]() pour
pour ![]() assez grand.
assez grand.
![]() M1. On peut chercher à déterminer
M1. On peut chercher à déterminer ![]() et ensuite on regarde si
et ensuite on regarde si ![]() .
.
![]() Lorsque les fonctions
Lorsque les fonctions ![]() et
et ![]() sont à valeurs dans
sont à valeurs dans ![]() , il suffit (lorsque les calculs sont simples) d’étudier les variations de
, il suffit (lorsque les calculs sont simples) d’étudier les variations de ![]() sur
sur ![]() , en faisant attention au signe de
, en faisant attention au signe de ![]() et en utilisant le tableau de variation, on détermine
et en utilisant le tableau de variation, on détermine ![]() .
.
![]() Lorsque les fonctions sont à valeurs dans
Lorsque les fonctions sont à valeurs dans ![]() , il suffit d’étudier la fonction
, il suffit d’étudier la fonction ![]() sur
sur ![]() (fonction à valeurs dans
(fonction à valeurs dans ![]() ) pour déterminer
) pour déterminer ![]() .
.
![]() Pour des fonctions à valeurs dans
Pour des fonctions à valeurs dans ![]() , il faudrait étudier la fonction
, il faudrait étudier la fonction ![]() sur
sur ![]() .
.
On peut choisir une base ![]() de
de ![]() et chercher à étudier la convergence uniforme sur
et chercher à étudier la convergence uniforme sur ![]() des suites de coordonnées
des suites de coordonnées ![]() pour
pour ![]() vers la
vers la ![]() -ème coordonnée
-ème coordonnée ![]() de
de ![]() dans la base
dans la base ![]() et choisir une norme sur
et choisir une norme sur ![]() utilisant cette base.
utilisant cette base.
Exemple
On note si ![]() .
.
Convergence simple et uniforme de la suite de fonctions.
![]() M2. Pour
M2. Pour ![]() , on peut chercher
, on peut chercher ![]() tel que
tel que ![]()
(resp. ![]() ), la suite
), la suite ![]() étant convergente vers 0.
étant convergente vers 0.
Dans les deux cas, ![]() ,
, ![]() .
.
Exemple
Soit si ![]() et
et ![]() ,
, ![]() .
.
Convergence simple et uniforme.
(soit selon le cas,
2. Comment prouver qu’une suite de fonctions ne converge pas uniformément sur  ?
?
![]() M1. Si
M1. Si ![]() n’est pas bornée sur
n’est pas bornée sur ![]() pour
pour ![]() assez grand, la suite
assez grand, la suite ![]() ne converge pas uniformément vers
ne converge pas uniformément vers ![]() sur
sur ![]() .
.
Dans la suite, on suppose que les fonctions ![]() sont bornées sur
sont bornées sur ![]() pour
pour ![]() assez grand.
assez grand.
![]() M2. On démontre que la suite
M2. On démontre que la suite ![]() ne converge pas vers 0.
ne converge pas vers 0.
Dans le cas particulier où ![]() et
et ![]() sont à valeurs dans
sont à valeurs dans ![]() , il suffit d’étudier
, il suffit d’étudier ![]() et de démontrer que la suite
et de démontrer que la suite ![]() ne converge pas vers 0.
ne converge pas vers 0.
Exemple
Appliquer M2 à ![]() .
.
![]() M3. Il suffit de trouver une suite
M3. Il suffit de trouver une suite ![]() de points de
de points de ![]() telle que la suite
telle que la suite ![]() ne converge pas vers 0.
ne converge pas vers 0.
Exemple
Appliquer M3 à ![]() .
.
![]() M4. Si pour tout
M4. Si pour tout ![]() ,
, ![]() est continue sur
est continue sur ![]() et s’il existe
et s’il existe ![]() tel que
tel que ![]() est discontinue en
est discontinue en ![]() , la suite
, la suite ![]() ne converge pas uniformément vers
ne converge pas uniformément vers ![]() . (S’il y avait convergence uniforme,
. (S’il y avait convergence uniforme, ![]() devrait aussi être continue.).
devrait aussi être continue.).
Exemple
Appliquer M4 à ![]() .
.
![]() M5. Lorsque la suite de fonctions continues
M5. Lorsque la suite de fonctions continues ![]() converge vers la fonction continue
converge vers la fonction continue ![]() sur
sur ![]() , s’il existe
, s’il existe ![]() où
où ![]() et tel que
et tel que ![]() , la suite
, la suite ![]() ne converge pas uniformément vers
ne converge pas uniformément vers ![]() sur
sur ![]() .
.
Exemple
Appliquer M5 à ![]() sur
sur ![]() .
.
![]() M6. On démontre que le théorème de la double limite ne s’applique pas :
M6. On démontre que le théorème de la double limite ne s’applique pas :
c’est à dire ![]() étant une borne de l’intervalle
étant une borne de l’intervalle ![]() (resp. un point adhérent à
(resp. un point adhérent à ![]() on démontre que pour tout
on démontre que pour tout ![]() ,
, ![]() a une limite
a une limite ![]() finie (resp. dans
finie (resp. dans ![]() ) en
) en ![]() , et on démontre que la suite
, et on démontre que la suite ![]() ne converge pas, ou que la limite simple
ne converge pas, ou que la limite simple ![]() de la suite
de la suite ![]() n’admet pas
n’admet pas ![]() pour limite en
pour limite en ![]() .
.
Exemple
Appliquer M6 à la suite de fonctions définies pour ![]() et
et ![]() par
par ![]() .
.
COURS DE MATHS A DOMICILE
Les meilleurs profs de maths pour
réussir sa scolarité
En ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
3. Comment utiliser la convergence uniforme d’une suite de fonctions ?
![]() M1. Continuité : Si la suite de fonctions continues
M1. Continuité : Si la suite de fonctions continues ![]() converge uniformément vers
converge uniformément vers ![]() sur
sur ![]() , la fonction
, la fonction ![]() est continue sur
est continue sur ![]() .
.
![]() M1B. Pour démontrer que
M1B. Pour démontrer que ![]() est continue sur
est continue sur ![]() , il suffit de montrer que
, il suffit de montrer que ![]() est une suite de fonctions continues sur
est une suite de fonctions continues sur ![]() qui converge uniformément sur tout segment de
qui converge uniformément sur tout segment de ![]() (resp. au voisinage de tout point
(resp. au voisinage de tout point ![]() ) vers
) vers ![]() .
.
![]() M2. On peut alors appliquer le théorème de la double limite : Si
M2. On peut alors appliquer le théorème de la double limite : Si ![]() est une borne de l’intervalle
est une borne de l’intervalle ![]() (resp. un point adhérent à
(resp. un point adhérent à ![]() ), si la suite de fonctions
), si la suite de fonctions ![]() converge uniformément vers
converge uniformément vers ![]() sur
sur ![]() et si pour tout
et si pour tout ![]() de
de ![]() ,
, ![]() où
où ![]() (resp dans
(resp dans ![]() ), alors
), alors ![]() admet une limite en
admet une limite en ![]() et
et ![]()
![]() M3. Intégrale sur un segment :
M3. Intégrale sur un segment :
Si ![]() est une suite de fonctions continues sur l’intervalle
est une suite de fonctions continues sur l’intervalle ![]() qui converge uniformément sur tout segment de
qui converge uniformément sur tout segment de ![]() vers la fonction
vers la fonction ![]() , lorsque
, lorsque ![]() et
et ![]() sont éléments de
sont éléments de ![]() ,
,
![]() .
.
![]() M4. Dérivabilité :
M4. Dérivabilité :
On prouve que
![]() pour tout
pour tout ![]() de
de ![]() ,
, ![]() est de classe
est de classe ![]() sur l’intervalle
sur l’intervalle ![]() ,
,
![]() la suite
la suite ![]() converge simplement sur
converge simplement sur ![]() vers la fonction
vers la fonction ![]() ,
,
![]() la suite de fonctions
la suite de fonctions ![]() converge uniformément vers
converge uniformément vers ![]() sur tout segment de
sur tout segment de ![]() .
.
Alors ![]() est de classe
est de classe ![]() sur
sur ![]() et
et ![]() .
.
![]() M5. Fonctions de classe
M5. Fonctions de classe ![]() où
où ![]()
On prouve que
![]() pour tout
pour tout ![]() de
de ![]() ,
, ![]() est de classe
est de classe ![]() sur l’intervalle
sur l’intervalle ![]() ,
,
![]() pour tout
pour tout ![]() , la suite de fonctions
, la suite de fonctions ![]() converge simplement sur
converge simplement sur ![]() vers une fonction
vers une fonction ![]()
![]() la suite de fonctions
la suite de fonctions ![]() converge uniformément sur tout segment de
converge uniformément sur tout segment de ![]() vers une fonction
vers une fonction ![]() .
.
Alors ![]() est de classe
est de classe ![]() sur I et pour tout
sur I et pour tout ![]() ,
, ![]() .
.
![]() M6. Le théorème de convergence dominée (chapitre intégration sur un intervalle quelconque) permet d’intervertir, sous certaines conditions, l’intégrale et la limite (sans avoir besoin de la convergence uniforme).
M6. Le théorème de convergence dominée (chapitre intégration sur un intervalle quelconque) permet d’intervertir, sous certaines conditions, l’intégrale et la limite (sans avoir besoin de la convergence uniforme).
Il y a deux théorèmes écrivant une fonction ![]() comme limite uniforme.
comme limite uniforme.
![]() M7. Théorème de Weierstrass : Toute fonction
M7. Théorème de Weierstrass : Toute fonction ![]() continue sur
continue sur ![]() à valeurs dans
à valeurs dans ![]() est limite uniforme sur
est limite uniforme sur ![]() d’une suite de fonctions polynômes à coefficients dans
d’une suite de fonctions polynômes à coefficients dans ![]() .
.
![]() M8. Toute fonction continue par morceaux sur
M8. Toute fonction continue par morceaux sur ![]() à valeurs dans
à valeurs dans ![]() est limite uniforme sur
est limite uniforme sur ![]() d’une suite de fonctions en escalier sur
d’une suite de fonctions en escalier sur ![]() .
.
Les étudiants en Maths Spé, peuvent se servir des cours en ligne de maths en PSI, des cours en ligne en PC de Maths ou des cours en ligne de Maths en MP et des cours de maths à domicile pour compléter leurs révisions en vue des concours des écoles d’ingénieurs.
4. Comment étudier la convergence d’une série de fonctions ?
Les questions à se poser quand on demande d’étudier la convergence de la série de fonctions de terme général ![]() sur l’intervalle
sur l’intervalle ![]() .
.
![]() Q1. La série est-elle simplement convergente sur
Q1. La série est-elle simplement convergente sur ![]() ? Si ce n’est pas le cas, on se place sur un intervalle
? Si ce n’est pas le cas, on se place sur un intervalle ![]() tel que
tel que ![]() sur lequel la série de fonctions de terme général
sur lequel la série de fonctions de terme général ![]() converge simplement.
converge simplement.
![]() Q2. La série est-elle normalement convergente sur
Q2. La série est-elle normalement convergente sur ![]() ? Si oui, l’étude de la convergence est terminée, car la série est uniformément convergente sur
? Si oui, l’étude de la convergence est terminée, car la série est uniformément convergente sur ![]() .
.
![]() Q3. Si la série n’est pas normalement convergente sur
Q3. Si la série n’est pas normalement convergente sur ![]() , on cherche si
, on cherche si ![]() .
.
![]() Si la suite
Si la suite ![]() ne converge pas vers 0, il ne peut y avoir convergence uniforme.
ne converge pas vers 0, il ne peut y avoir convergence uniforme.
![]() Si la suite
Si la suite ![]() converge vers 0, on peut étudier la convergence uniforme : dans ce cas, on regarde si
converge vers 0, on peut étudier la convergence uniforme : dans ce cas, on regarde si ![]() , où
, où ![]() est le reste d’ordre
est le reste d’ordre ![]() de la série de terme général
de la série de terme général ![]() .
.
Méthode d’étude :
![]() ET1. Étudier la convergence simple de la série, c.a.d. étudier la série de terme général
ET1. Étudier la convergence simple de la série, c.a.d. étudier la série de terme général ![]() : il s’agit d’un problème de convergence de série numérique (resp. de série vectorielle).
: il s’agit d’un problème de convergence de série numérique (resp. de série vectorielle).
Il suffit de prouver que la série converge absolument (c’est à dire que ![]() ou
ou ![]() selon la nature de l’ensemble d’arrivée, converge).
selon la nature de l’ensemble d’arrivée, converge).
![]() ET2. Pour étudier la convergence normale (lorsque les fonctions
ET2. Pour étudier la convergence normale (lorsque les fonctions ![]() sont bornées sur I) :
sont bornées sur I) :
![]() soit on calcule
soit on calcule ![]() (en étudiant éventuellement la fonction
(en étudiant éventuellement la fonction ![]() si elle est à valeurs dans
si elle est à valeurs dans ![]() , et
, et ![]() si elle est à valeurs dans
si elle est à valeurs dans ![]() ) et on démontre que
) et on démontre que ![]() converge.
converge.
![]() soit on trouve
soit on trouve ![]() tel que
tel que ![]() et tel que
et tel que ![]() converge (méthode à utiliser lorsque les variations de
converge (méthode à utiliser lorsque les variations de ![]() sont compliquées pour les fonctions à valeurs dans
sont compliquées pour les fonctions à valeurs dans ![]() ).
).
Il faudra peut-être restreindre l’intervalle et démontrer que la série converge normalement sur un intervalle (ou un ensemble) plus petit.
Pour des fonctions scalaires, il est inutile de vouloir étudier la convergence normale sur ![]() lorsqu’il existe
lorsqu’il existe ![]() tel que la série de terme général
tel que la série de terme général ![]() diverge, ou lorsque les fonctions
diverge, ou lorsque les fonctions ![]() ne sont pas bornées sur l’intervalle
ne sont pas bornées sur l’intervalle ![]() .
.
S’il existe ![]() tel que
tel que ![]() diverge, en écrivant
diverge, en écrivant ![]() , on démontre que
, on démontre que ![]() ne converge pas normalement sur
ne converge pas normalement sur ![]() .
.
Quelques méthodes de choix d’intervalle pour démontrer une convergence normale dans le cas de fonctions définies sur un intervalle réel
![]() l’intervalle de convergence simple noté
l’intervalle de convergence simple noté ![]() est ouvert : il est souvent nécessaire de se restreindre à un segment inclus dans
est ouvert : il est souvent nécessaire de se restreindre à un segment inclus dans ![]() .
.
![]() l’intervalle de convergence simple noté
l’intervalle de convergence simple noté ![]() est un intervalle centré en 0 : il est plus simple de démontrer que la série converge normalement sur un segment du type
est un intervalle centré en 0 : il est plus simple de démontrer que la série converge normalement sur un segment du type ![]() où
où ![]() .
.
![]() en étudiant les variations de
en étudiant les variations de ![]() (à valeurs réelles) sur
(à valeurs réelles) sur ![]() , on a trouvé
, on a trouvé ![]() tel que
tel que ![]() admette un maximum en
admette un maximum en ![]() et
et ![]() diverge, la fonction
diverge, la fonction ![]() changeant de sens de variation en
changeant de sens de variation en ![]() ,
,
… lorsque ![]() ou
ou ![]() prendre
prendre ![]() et
et ![]() , démontrer qu’il existe
, démontrer qu’il existe ![]() tel que si
tel que si ![]() et utiliser la monotonie de
et utiliser la monotonie de ![]() sur
sur ![]() pour prouver la convergence normale sur
pour prouver la convergence normale sur ![]() .
.
… lorsque ![]() ,introduire
,introduire ![]() , démontrer qu’il existe
, démontrer qu’il existe ![]() tel que si
tel que si ![]() et utiliser la monotonie de
et utiliser la monotonie de ![]() sur
sur ![]() pour prouver la convergence normale sur
pour prouver la convergence normale sur ![]() .
.
UN PROF DE MATHS POUR EXCELLER
La pratique et la compréhension
clés de la réussite
Cours de maths en ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
5. Comment utiliser la convergence uniforme d’une série de fonctions ?
Lorsque la série de fonctions de terme général ![]() est simplement convergente, on note
est simplement convergente, on note  .
.
![]() M1. Continuité : Si pour tout
M1. Continuité : Si pour tout ![]() ,
, ![]() est continue sur
est continue sur ![]() et si
et si ![]() converge uniformément sur tout segment inclus dans
converge uniformément sur tout segment inclus dans ![]() (resp. au voisinage de tout point
(resp. au voisinage de tout point ![]() ), la somme
), la somme ![]() est continue sur
est continue sur ![]() .
.
![]() M2. On peut alors appliquer le théorème de la double limite :
M2. On peut alors appliquer le théorème de la double limite :
Si ![]() est une borne de l’intervalle
est une borne de l’intervalle ![]() (resp.
(resp. ![]() est un point adhérent à
est un point adhérent à ![]() ), si la série de fonctions de terme général
), si la série de fonctions de terme général ![]() converge uniformément sur
converge uniformément sur ![]() et si pour tout
et si pour tout ![]() ,
, ![]() admet en
admet en ![]() une limite
une limite ![]() (resp.
(resp. ![]() ), alors
), alors 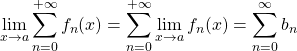 .
.
exemple
Si ![]() et
et ![]() ,
, ![]() étude de la limite de
étude de la limite de ![]() en
en ![]() .
.
![]() M3. Intégrale sur un segment : Si pour tout
M3. Intégrale sur un segment : Si pour tout ![]() ,
, ![]() est continue sur
est continue sur ![]() et si la série de terme général
et si la série de terme général ![]() converge uniformément sur
converge uniformément sur ![]() ,
, 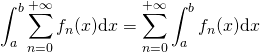 .
.
On verra un autre théorème permettant d’intervertir somme et intégrale avec une hypothèse de convergence simple. (cf chapitre intégration sur un intervalle quelconque).
![]() M4. Dérivabilité : si l’on prouve que :
M4. Dérivabilité : si l’on prouve que :
![]() pour tout
pour tout ![]() de
de ![]() ,
, ![]() est de classe
est de classe ![]() sur l’intervalle
sur l’intervalle ![]() ,
,
![]()
![]() converge simplement sur
converge simplement sur ![]() ,
,
![]()
![]() converge uniformément sur tout segment de
converge uniformément sur tout segment de ![]() ,
,
![]()
![]() la somme
la somme ![]() est de classe
est de classe ![]() sur
sur ![]() et
et 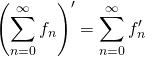 .
.
![]() M5. Fonctions de classe
M5. Fonctions de classe ![]() où
où ![]() : si l’on prouve que
: si l’on prouve que
![]() pour tout
pour tout ![]() de
de ![]() ,
, ![]() est de classe
est de classe ![]() sur l’intervalle
sur l’intervalle ![]() ,
,
![]() pour tout
pour tout ![]() ,
, ![]() converge simplement sur
converge simplement sur ![]() ,
,
![]()
![]() converge uniformément sur tout segment de
converge uniformément sur tout segment de ![]() ,
,
![]()
![]() la somme
la somme ![]() est de classe
est de classe ![]() sur
sur ![]() et
et 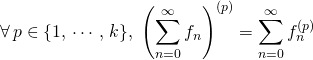 .
.
Application à l’exponentielle d’une matrice, d’un endomorphisme :
![]() A1 : Soit
A1 : Soit ![]() et
et ![]() .
.
a) On peut définir pour tout ![]() ,
, ![]() notée aussi
notée aussi ![]() .
.
La série converge normalement sur tout segment ![]() où
où ![]()
b) La fonction ![]() est de classe
est de classe ![]() sur
sur ![]() et pour tout
et pour tout ![]()
![]() .
.
![]() A2 : Soit
A2 : Soit ![]() un
un ![]() –espace vectoriel de dimension finie et
–espace vectoriel de dimension finie et ![]() .
.
a) On peut définir pour tout ![]() ,
, ![]() noté aussi
noté aussi ![]() .
.
La série converge normalement sur tout segment ![]() où
où ![]()
b) La fonction ![]() est de classe
est de classe ![]() sur
sur ![]() et pour tout
et pour tout ![]()
![]() .
.
En plus de ce cours en ligne sur les suites et séries de fonctions, de nombreux autres cours peuvent être retravaillés. En voici quelques exemples :
- l’intégration sur un intervalle quelconque
- les séries entières
- le dénombrement
- les intégrales à paramètre
- les variables aléatoires
Si vous souhaitez accéder à l’ensemble des méthodes et aux corrigés des exemples, n’hésitez pas à télécharger l’application PrepApp

