Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Cours en ligne Maths en Maths Spé
Chapitres Maths en MP, PSI, PC, TSI, PT
Cours sur les espaces vectoriels normés en MP, PC, PSI
Résumé de cours Exercices et corrigés
Résumé de cours et méthodes – Espaces vectoriels normés
1. Comment prouver que  est une norme sur
est une norme sur  ?
?
![]() M1. Commencer par démontrer que
M1. Commencer par démontrer que ![]() est bien défini et que
est bien défini et que ![]() (attention quand
(attention quand ![]() est défini en utilisant une borne supérieure, un maximum ou la somme d’une série).
est défini en utilisant une borne supérieure, un maximum ou la somme d’une série).
Puis prouver :
![]() (N1) : séparation
(N1) : séparation
Si ![]() ,
, ![]()
![]() (N2) : homogénéité
(N2) : homogénéité
![]()
![]() (N3) : inégalité triangulaire
(N3) : inégalité triangulaire
![]() .
.
![]() M2. Ici
M2. Ici ![]() . Montrer que
. Montrer que ![]() est une norme euclidienne (y penser lorsque
est une norme euclidienne (y penser lorsque ![]() s’exprime en fonction de la racine carrée d’une expression).
s’exprime en fonction de la racine carrée d’une expression).
Dans ce cas, il faut montrer qu’il existe un produit scalaire ![]() défini sur
défini sur ![]() vérifiant
vérifiant ![]() .
.
On peut trouver l’expression de ![]() en utilisant l’une des deux identités de polarisation :
en utilisant l’une des deux identités de polarisation :
![]()
ou ![]()
![]() M3. Soit
M3. Soit ![]() . Si pour tout
. Si pour tout ![]() ,
, ![]() est une norme sur
est une norme sur ![]() , les applications
, les applications ![]() ,
, ![]() et
et ![]() :
: ![]() , définies pour
, définies pour ![]() où
où ![]() par
par
![]()
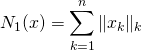
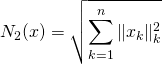 .
.
sont des normes sur ![]() telles que pour tout
telles que pour tout ![]() ,
,
![]() .
.
(s’applique pour ![]() et
et ![]() , donc
, donc ![]() ).
).
![]() M4. Utiliser les normes au programme.
M4. Utiliser les normes au programme.
![]() M4.1. La norme de la convergence uniforme sur l’espace vectoriel
M4.1. La norme de la convergence uniforme sur l’espace vectoriel ![]() des fonctions bornées sur
des fonctions bornées sur ![]() à valeurs dans
à valeurs dans ![]() :
:
si ![]() ,
, ![]()
![]() M4.2. Sur l’espace vectoriel des suites bornées à valeurs dans
M4.2. Sur l’espace vectoriel des suites bornées à valeurs dans ![]()
lorsque ![]() ,
, ![]() .
.
2. Comment étudier l’équivalence des normes ?
![]() M1. Pour prouver que deux normes
M1. Pour prouver que deux normes ![]() et
et ![]() sur le
sur le ![]() -espace vectoriel
-espace vectoriel ![]() sont équivalentes, il faut trouver deux réels
sont équivalentes, il faut trouver deux réels ![]() et
et ![]() strictement positifs tels que :
strictement positifs tels que : ![]() .
.
![]() M2. En dimension finie, toutes les normes sont équivalentes : il n’y a rien à faire sauf si l’on demande des valeurs de
M2. En dimension finie, toutes les normes sont équivalentes : il n’y a rien à faire sauf si l’on demande des valeurs de ![]() et
et ![]() .
.
![]() M3. En dimension infinie, pour prouver que deux normes
M3. En dimension infinie, pour prouver que deux normes ![]() et
et ![]() ne sont pas équivalentes, il suffit de trouver une suite
ne sont pas équivalentes, il suffit de trouver une suite
![]() de
de ![]() telle que
telle que ![]() ou telle que
ou telle que ![]() .
.
Les notions conservées pour des normes équivalentes : suite convergente et sa limite, point adhérent, point intérieur, ouvert, fermé, ensemble borné, limite, continuité.
PROF DE MATHS PARTICULIER
Des cours de qualité et enseignants aguerris
Préparer des concours ou s'exercer
Avis Google France ★★★★★ 4,9 sur 5
3. Comment prouver qu’une suite d’un  -e.v.n. converge ?
-e.v.n. converge ?
Lorsque ![]() n’est pas de dimension finie, l’énoncé introduit une norme
n’est pas de dimension finie, l’énoncé introduit une norme ![]() sur
sur ![]() .
.
Lorsque ![]() est de dimension finie, on peut choisir une norme particulière simplifiant les calculs.
est de dimension finie, on peut choisir une norme particulière simplifiant les calculs.
Pour démontrer que la suite ![]() converge dans
converge dans ![]() :
:
![]() M1. Trouver
M1. Trouver ![]() de
de ![]() tel que la suite de réels
tel que la suite de réels ![]() converge vers 0.
converge vers 0.
![]() M2. Trouver
M2. Trouver ![]() de
de ![]() tel que
tel que
![]()
![]() .
.
![]() M3. Si
M3. Si ![]() est un
est un ![]() -espace vectoriel de dimension finie, on peut introduire une base
-espace vectoriel de dimension finie, on peut introduire une base ![]() de
de ![]() et en écrivant
et en écrivant 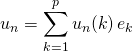 , montrer que pour tout
, montrer que pour tout ![]() , la suite de scalaires
, la suite de scalaires ![]() converge dans
converge dans ![]() .
.
Cette méthode peut être utilisée en particulier pour étudier la limite d’une suite ![]() de matrices de type
de matrices de type ![]() , en étudiant, pour tout couple
, en étudiant, pour tout couple ![]() où
où ![]() , la limite de la suite
, la limite de la suite ![]() , où
, où ![]() est le terme de la ligne
est le terme de la ligne ![]() et colonne
et colonne ![]() de
de ![]() :
:
La suite ![]() converge ssi pour tout
converge ssi pour tout ![]() de
de ![]() , la suite
, la suite ![]() converge.
converge.
Dans ce cas, ![]() .
.
![]() M4. En appliquant les résultats usuels sur les opérations sur les suites convergentes.
M4. En appliquant les résultats usuels sur les opérations sur les suites convergentes.
Pour aller plus loin dans les révisions et pourquoi pas prendre de l’avance sur les cours enseignés en classe en prépa, jetez un œil sur les différents cours en ligne de Maths en PSI, les cours en ligne de Maths en PC et aussi les cours en ligne de Maths en MP.
4. Comment raisonner avec les valeurs d’adhérence d’une suite ?
Lorsque ![]() n’est pas de dimension finie, l’énoncé introduit une norme
n’est pas de dimension finie, l’énoncé introduit une norme ![]() sur
sur ![]() . Lorsque
. Lorsque ![]() est de dimension finie, on peut choisir la norme dans
est de dimension finie, on peut choisir la norme dans ![]() , la notion de valeur d’adhérence ne dépend pas de la norme choisie.
, la notion de valeur d’adhérence ne dépend pas de la norme choisie.
![]() Def.
Def. ![]() est une valeur d’adhérence de la suite
est une valeur d’adhérence de la suite ![]() de
de ![]() si, et seulement si, il existe une suite extraite
si, et seulement si, il existe une suite extraite
![]() qui converge vers
qui converge vers ![]() .
.
![]() U1. Une suite ayant au moins deux valeurs d’adhérence distinctes diverge.
U1. Une suite ayant au moins deux valeurs d’adhérence distinctes diverge.
![]() U2. Théorème de Bolzano- Weierstrass : toute suite réelle bornée admet une valeur d’adhérence.
U2. Théorème de Bolzano- Weierstrass : toute suite réelle bornée admet une valeur d’adhérence.
![]() U3. Une suite bornée d’un espace vectoriel de dimension finie converge si, et seulement si, elle a une unique valeur d’adhérence.
U3. Une suite bornée d’un espace vectoriel de dimension finie converge si, et seulement si, elle a une unique valeur d’adhérence.
![]() U4. Une partie non vide
U4. Une partie non vide ![]() est un compact si, et seulement si, toute suite de
est un compact si, et seulement si, toute suite de ![]() admet une valeur d’adhérence.
admet une valeur d’adhérence.
![]() U5. Une suite d’éléments d’une partie compacte converge si, et seulement si, elle admet une unique valeur d’adhérence.
U5. Une suite d’éléments d’une partie compacte converge si, et seulement si, elle admet une unique valeur d’adhérence.
![]() U6. Une suite bornée d’un espace vectoriel de dimension finie converge si, et seulement si, elle a une unique valeur d’adhérence.
U6. Une suite bornée d’un espace vectoriel de dimension finie converge si, et seulement si, elle a une unique valeur d’adhérence.
5. Comment raisonner avec des points adhérents ?
Lorsque ![]() n’est pas de dimension finie, l’énoncé introduit une norme
n’est pas de dimension finie, l’énoncé introduit une norme ![]() sur
sur ![]() ; lorsque
; lorsque ![]() est de dimension finie, on peut choisir la norme dans
est de dimension finie, on peut choisir la norme dans ![]() .
.
Pour démontrer que ![]() est adhérent à la partie non vide
est adhérent à la partie non vide ![]() (lorsque
(lorsque ![]() ) :
) :
![]() M1. démontrer qu’il existe une suite
M1. démontrer qu’il existe une suite ![]() de points de
de points de ![]() qui converge vers
qui converge vers ![]() .
.
![]() M2. démontrer que
M2. démontrer que ![]() .
.
![]() M3. L’adhérence de
M3. L’adhérence de ![]() , notée
, notée ![]() , est l’ensemble des points adhérents à
, est l’ensemble des points adhérents à ![]() , elle contient
, elle contient ![]() .
.
C’est le plus petit fermé de ![]() contenant
contenant ![]() .
.
![]() M4. Une partie
M4. Une partie ![]() de
de ![]() est dense dans
est dense dans ![]() lorsque
lorsque ![]() .
.
Exemples :
L’adhérence de ![]() est
est ![]() .
.
![]() est dense dans
est dense dans ![]() .
.
Certains étudiants de Maths Spé se relâchent considérablement lorsqu’ils ne sont pas suivis en cours de soutien de maths ou lors d’un stage de maths spé de révision. Ainsi, pour éviter ce relâchement et rester à un bon niveau, les étudiants sont vivement incités à consulter les cours en ligne ainsi que les exercices corrigés au programme de Maths Spé, comme :
- les suites et séries de fonctions
- l’intégration sur un intervalle quelconque
- les séries entières
- le dénombrement
- les intégrales à paramètre
Si vous souhaitez accéder à l’ensemble des méthodes et aux corrigés des exemples, n’hésitez pas à télécharger l’application PrepApp

