Chapitres du sous-test 2 du Tage Mage

Théorème de Pythagore exercice corrigé

Name: Groupe Réussite: Cours particuliers, stages intensifs de révision
Brand: Groupe Réussite
SKU: Cours Particuliers
Rating: 4.8 (1000 reviews)

Résumé de cours Exercices et corrigés

Cours en ligne du Tage Mage

Le théorème de Pythagore tombe presque chaque année au brevet, c’est donc un incontournable pour les élèves préparant le brevet, mais aussi pour les étudiants préparant le Tage Mage ou le Score Message. Le théorème de Pythagore est en effet le théorème le plus important en géométrie avec le théorème de Thales. Il est donc conseillé non seulement de le connaître par cœur, mais aussi de savoir l’appliquer dans le cadre d’exercices. Pour mieux comprendre et utiliser le théorème de Pythagore, vous pouvez faire appel aux cours particuliers en maths via Groupe Réussite. Les profs de maths vous aideront à saisir le théorème de Pythagore et à vous entraîner à son application via des exercices Pythagore lors de vos cours de maths.

Exercices Théorème de Pythagore

1 – Exercice théorème de Pythagore : calcul d’un côté

Soit IYS un triangle rectangle en Y tel que :
SI = 13,5 cm et SY = 10,8 cm.
Calculer la longueur IY .

2 – Exercice Pythagore : nature d’un triangle

a) Soit CXL un triangle tel que : CL = 15,9 cm , CX = 13,5 cm et LX = 8,4 cm.
Quelle est la nature du triangle CXL ?

b) Soit BIK un triangle tel que : KI = 14 cm , IB = 8,4 cm et KB = 11,2 cm.
Quelle est la nature du triangle BIK ?

c) Soit EVG un triangle tel que : VE = 9,2 cm , VG = 11,5 cm et GE = 6,9 cm.
Quelle est la nature du triangle EVG ?

3 – Exercice Théorème de Pythagore en Mésopotamie

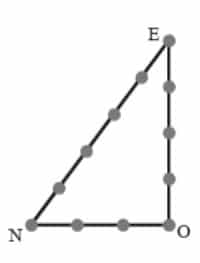
En Mésopotamie, pendant l’antiquité on utilisait des cordes à nœuds (avec une distance de 1 m entre chaque nœud) pour obtenir des angles droits dans les constructions notamment d’autels religieux. Explique pourquoi cette corde à nœuds bien tendue donne un angle droit.

4 – Exercice Pythagore : calculer un côté

a) Soit CFN un triangle rectangle en N tel que :
CF = 18,2 cm et CN = 16,8 cm.
Calculer la longueur FN .

b) Soit RGX un triangle rectangle en R tel que :
XR = 3,6 cm et GR = 1,5 cm.
Calculer la longueur XG.

5 – Exercice theoreme de Pythagore : Cercle

Soit $\mathcal{C}$ de diamètre [TW] et P est un point de $\mathcal{C}$

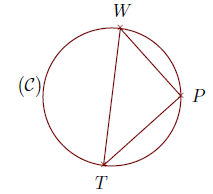
On donne WP = 4,8 cm et TP = 5,5 cm

Calculer la longueur TW

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

Avis Google France ★★★★★ 4,9 sur 5

Corrigés sur le théorème de Pythagore

Corrigé de l’exercice 1 avec le théorème de Pythagore

Soit IYS un triangle rectangle en Y tel que :
SI = 13,5 cm et SY = 10,8 cm.
Calculer la longueur IY .
Le triangle IYS est rectangle en Y.
Son hypoténuse est [SI], d’après le théorème de Pythagore :
$SI² = IY² + SY²$
$IY² = SI² − SY²$
$IY² = 13,5^2 − 10,8^2$
$IY² = 182,25 − 116,64$
$IY² = 65,61$
Donc IY = $\sqrt{65,61}$ = 8,1 cm

Corrigé de l’exercice 2 par le théorème de Pythagore

a) Le triangle CXL n’est ni isocèle, ni équilatéral.
$\bullet$ CL² = 15,9² = 252,81 ([CL] est le plus grand côté.)
$\bullet$ LX² + CX² = 8,4² + 13,5² = 252,81
Donc CL² = LX² + CX².
D’après la réciproque du théorème de Pythagore, le triangle CXL est rectangle en X .

b) Le triangle BIK n’est ni isocèle, ni équilatéral.
$\bullet$ KI² = 14² = 196 ([KI] est le plus grand côté.)
$\bullet$ IB² + KB² = 8,4² + 11,2² = 196
Donc KI² = IB² + KB².
D’après la réciproque du théorème de Pythagore, le triangle BIK est rectangle en B

c)Le triangle EVG n’est ni isocèle, ni équilatéral.
$\bullet$ VG² = 11,5² = 132,25 ([VG] est le plus grand côté.)
$\bullet$ EV² + EG² = 9,2² + 6,9² = 84,64 + 47,61 = 132,25
Donc VG² = EV² + EG².
D’après la réciproque du théorème de Pythagore, le triangle EVG est rectangle en E

Corrigé de l’exercice 3 : théorème de Pythagore avec des cordes

Dans le triangle ONE, on a : NE² = 5² = 25 et NO² + OE² = 3² + 4² = 9 + 16 = 25
Comme NE² = NO² + OE² , alors d’après la réciproque du théorème de Pythagore
le triangle NOE est rectangle en O.

Corrigé de l’exercice 4 : calcul d’un côté avec Pythagore

a) Le triangle CFN est rectangle en N. Son hypoténuse est [CF].
D’après le théorème de Pythagore :
CF² = FN² + CN²
FN² = CF² − CN² (On cherche FN)
FN² = 18,2² − 16,8²
FN² = 331,24 − 282,24
FN² = 49
Donc FN = $\sqrt{49}$ = 7 cm

b) Le triangle RGX est rectangle en R.
Son hypoténuse est [XG].
D’après le théorème de Pythagore :
XG² = GR² + XR²
XG² = 1,5² + 3,6²
XG² = 2,25 + 12,96
XG² = 15,21
Donc XG = $\sqrt{15,21}$ = 3,9 cm

Corrigé de l’exercice 5 : cercle et théorème de Pythagore

[TW] est le diamètre du cercle circonscrit au triangle TWP.
Donc le triangle TWP est rectangle en P. [TW] est l’hypoténuse de ce triangle.
D’après le théorème de Pythagore, nous avons :
TW² = WP² + TP²
TW² = 4,8² + 5,5²
TW² = 23,04 + 30,25
TW² = 53,29

Donc TW = $\sqrt{53,29}$ = 7,3 cm.

COURS PARTICULIERS EN LIGNE

Nous avons sélectionné pour vous les meilleurs professeurs particuliers.

POUR ACCÉLÉRER MA PROGRESSION