Chapitres du sous-test 2 du Tage Mage

Cours sur les figures géométriques : définitions et exemples

Name: Groupe Réussite: Cours particuliers, stages intensifs de révision
Brand: Groupe Réussite
SKU: Cours Particuliers
Rating: 4.8 (1000 reviews)

Résumé de cours Exercices et corrigés

Cours en ligne du Tage Mage

Si les figures géométriques les plus simples et leurs noms sont connus dès le plus jeune âge, il y a néanmoins des figures plus complexes ainsi que leurs propriétés à connaître ensuite notamment pour la préparation du bac. Tout étudiant préparant le Tage Mage ou préparant le Gmat doit savoir retrouver le périmètre, l’aire et le volume de ces figures. Pour maîtriser totalement la géométrie pour le Tage Mage ou dans vos études supérieures, alors nous vous recommandons de prendre des cours de maths à domicile.

Figures géométriques importantes :

Certaines figures ont des propriétés intéressantes, elles tiennent donc une place prépondérante au Tage Mage, c’est notamment le cas des suivantes :

Le carré

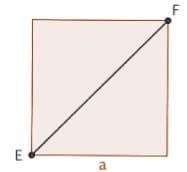
Si un carré est de côté $a$ , alors :

$\bullet$ Périmètre = $4a$
$\bullet$ Aire = $a^2$
$\bullet$ Diagonale : EF = $a\sqrt{2}$

Le triangle équilatéral

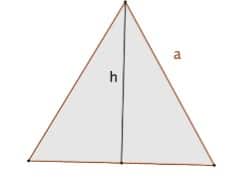
Les 3 côtés sont égaux et les 3 angles égaux à 60° chacun.

Si un triangle équilatéral est de côté $a$ , alors :

$\bullet$ Hauteur = $\dfrac {a \sqrt{3}}{2}$
$\bullet$ Aire = $\dfrac {a^2 \sqrt{3}}{4}$

Le cercle

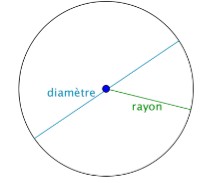
Cercle de rayon $r$

$\bullet$ Périmètre = $2 \times \pi \times r$ ou Diamètre $\times \pi$

$\bullet$ Aire = $\pi \times r^2$

Le cube

Si un cube est de côté $a$ , alors :

$\bullet$ Volume = $a^3$
$\bullet$ Grande diagonale KJ = $a \sqrt{3}$
$\bullet$ Aire latérale = $6a^2$ (l’aire des 6 faces)

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

Avis Google France ★★★★★ 4,9 sur 5

Agrandissement réduction

Si les longueurs sont multipliées par un nombre $k$ , alors :

$\bullet$ Aires $\times k^2$
$\bullet$ Volumes $\times k^3$

Exemple :

Dans un carton, on peut mettre 45 boîtes identiques. Si on double les dimensions de ce carton, combien de boîtes pourra-t-on y mettre ?

A) 90

B) 135

C) 180

D) 360

E) 720

Réponse :

Toutes les longueurs sont doublées ( $\times 2$ ), donc la capacité (le volume) est multipliée par $2^3 = 8$ .
On pourra donc mettre $45 \times 8$ boîtes autrement dit 360, réponse D.

Polygones réguliers

Un polygone est régulier si tous ses côtés sont égaux et tous ses angles sont égaux.

Exemples de polygones réguliers :

$\bullet$ Triangle équilatéral : 3 côtés

$\bullet$ Pentagone : 5 côtés

$\bullet$ Hexagone : 6 côtés

$\bullet$ Octogone : 8 côtés

Pour un polygone régulier à $n$ côtés :

$\bullet$ La somme des $n$ angles vaut : $(n-2) \times 180$
$\bullet$ Chaque angle mesure : $\dfrac {(n-2) \times 180}{n}$
$\bullet$ Chaque angle au centre mesure : $\dfrac {360}{n}$
$\bullet$ Le nombre de diagonales est : $\dfrac {n(n-3)}{2}$

Les quadrilatères :

$\bullet$ Propriété du parallélogramme (plg) :

Les diagonales qui se coupent en leur milieu.

Les côtés opposés sont parallèles 2 à 2 (ou égaux 2 à 2).

$\bullet$ Propriétés du rectangle, en plus de celles du parallélogramme :

Les diagonales sont égales.

Les angles sont droit.

$\bullet$ Propriétés du losange, en plus de celles du parallélogramme :

Les diagonales sont perpendiculaires.

Les deux côtés consécutifs sont égaux.

$\bullet$ Propriétés du carré :

Le carré vérifie les propriétés du rectangle ainsi que les propriétés du losange.

COURS PARTICULIERS EN LIGNE

Nous avons sélectionné pour vous les meilleurs professeurs particuliers.

POUR ACCÉLÉRER MA PROGRESSION

Avis Google France ★★★★★ 4,9 sur 5

Conversion en géométrie figure

Il est indispensable d’être à l’aise en conversion et notamment la transition des m $^3$ vers les litres. Voici un rappel des tableaux.

Unités de longueurs

Unités d’aires ou de surfaces

Unités de volumes ou de contenances

A retenir : $1 dm^3 = 1$ litre et $1000$ litres = $1 m^3$

Exemple :

Un jerricane est rempli de jus et a pour dimension : 40 cm de largeur, 25 cm de profondeur et 80 cm de hauteur. Combien de verres de capacité 20 cl pourrait-on remplir avec ce jerricane ?

Réponse :

Il faut tout d’abord calculer le volume du jerricane, le convertir en litre voire en centilitre avant de diviser par 20 cl pour voir combien de fois on peut remplir 20 cl.

Le jerricane est considéré comme un pavé droit.

Donc le volume vaut : $40 \times 25 \times 80 = 80 000 cm^3$ . On convertit en $dm^3$ à l’aide du tableau ou en retenant qu’il faut enlever 3 zéros étant donné qu’on est dans « le monde » des volumes.

Donc pour passer d’une unité à l’autre on ajoute ou enlève 3 zéros (ou on décale la virgule de 3 rangs).

On a donc Volume $= 80 000 cm^3 = 80 dm^3 = 80$ litres.

On dispose donc de 80 litres que l’on veut servir dans des verres de 20 cl. Or 5 verres représentent 1 litre ( $5 \times 20$ cl). On a 80 litres, on pourra donc remplir $5 \times 80$ soit 400 verres avec ce jerricane.

Sinon le calcul « pur » était : 80 litres = 8 000 cl. On divise 8 000 par 20 = $400$ verres.

Plusieurs autres cours en ligne au programme du sous-test 2 du Tage Mage sont également disponibles et consultables gratuitement :