Chapitres du sous-test 2 du Tage Mage

Probabilité : cours et formules de probabilité de base

Name: Groupe Réussite: Cours particuliers, stages intensifs de révision
Brand: Groupe Réussite
SKU: Cours Particuliers
Rating: 4.8 (1000 reviews)

Résumé de cours Exercices et corrigés

Cours en ligne du Tage Mage

Les probabilités accompagnent les élèves tout au long de leur scolarité, du collège à la préparation du bac pour certains, mais aussi jusqu’en prépa et pas uniquement en MPSI ou PCSI et prépa HEC. De plus, l’étude des probabilités commence très tôt, en primaire, pour les plus précoces. Il est donc capital de comprendre les bases de ce domaine de cours de mathématiques, ce qui pourra vous servir même en dehors des cours dans la vie quotidienne. Pour une meilleure compréhension et maîtrise des probabilités au Tage Mage, nous vous recommandons de prendre des cours de maths à domicile. Ces cours sont dispensés par des profs de maths experts qui vous apporteront toutes les méthodes de travail efficaces pour réussir au concours.

Formule probabilité de base :

proba = $\dfrac {nombre~de~cas~favorables}{nombre~de~cas~total}$

Exemple type pour illustrer :

Une urne contient des boules numérotées de 1 à 40. On en tire une au hasard, quelle est la probabilité que ce soit une boule portant un multiple de 3 impair ?

Réponse :

On applique la formule ci-dessus :

Nombre total de cas : 40 (car 40 boules dans l’urne).
Nombre de cas favorables : les multiples de 3 qui sont impairs : 3 ; 9 ; 15 ; 21 ; 27 ; 33 ; 39. Il y en a 7.

Donc la probabilité voulue vaut $\dfrac {7}{40}$ .

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

Avis Google France ★★★★★ 4,9 sur 5

Tirage sans remise en probabilités : Attention le total change !

Exemple type pour illustrer le tirage sans remise :

Une urne contient 4 boules rouges, 5 noires et 6 vertes. On tire au hasard et sans remise deux boules de l’urne. Quelle est la probabilité d’obtenir deux boules noires ?

Réponses :

Il faut bien comprendre qu’on va multiplier les probabilités : celle d’avoir une noire au 1er tirage avec celle d’avoir une noire au 2nd tirage. Mais attention, pour le second tirage, la boule noire tirée n’a pas été remise dans l’urne.

1er tirage : il y 15 boules au total et 5 noires, la probabilité d’en tirer une vaut $\dfrac {5}{15}$
2nd tirage, il ne reste que 14 boules au total et plus que 4 noires, la probabilité d’en tirer une vaut $\dfrac {4}{14}$

Donc la probabilité de tirer deux boules noires vaut : $\dfrac {5}{15}$ $\times$ $\dfrac {4}{14}$

On peut simplifier le calcul : $\dfrac {5}{15}$ $\times$ $\dfrac {4}{14}$ = $\dfrac {1}{3}$ $\times$ $\dfrac {2}{7}$ = $\dfrac{2}{21}$ .

Obtenir au moins un… réflexe à avoir en probabilités !

Si dans un énoncé, on lit : « au moins un… », il faut penser à prendre l’événement contraire :

Si on note A un événement et $\overline{A}$ son contraire on a :

$\mathrm{P}(\overline{A})$ = 1 – $\mathrm{P}(A)$

Dans cette classe, au moins un élève aime les cours de maths. Le contraire de cette proposition est : dans cette classe, aucun élève n’aime les maths.

Donc le contraire de au moins un fait… est personne ne fait…Cette notion est à maîtriser pour le sous test 3 du Tage Mage et évidemment pour le programme de maths de terminale.

Exemple type pour illustrer les événements contraires :

Une famille est composée de 3 enfants, quelle est la probabilité qu’il y ait au moins une fille ?

Réponse :

Sans plus d’indication, on prend pour vrai qu’on a une chance sur deux d’avoir un garçon (ou une fille) à la naissance.

Le contraire d’obtenir au moins une fille est : ne pas obtenir de fille, autrement dit avoir 3 garçons.

On utilise la formule : P (au moins une fille) = 1 – P (aucune fille)

Or la probabilité d’avoir un garçon vaut 1/2, donc d’en avoir 3 :

$\dfrac {1}{2}$ $\times$ $\dfrac {1}{2}$ $\times$ $\dfrac{1}{2}$ = $\dfrac {1}{8}$

Et donc la probabilité d’avoir au moins une fille vaut :

1 – $\dfrac {1}{8}$ = $\dfrac {8}{8}$ – $\dfrac{1}{8}$ = $\dfrac{7}{8}$

Union et Intersection en probabilités : cours

L’union ∪ signifie : ou (non exclusif) c’est-à-dire soit l’un, soit l’autre, soit les deux. C’est un et/ou.

L’intersection ∩ signifie : et dans le sens de : à la fois, simultanément, ce qu’il y a en commun.

Formules de proba : L’union et l’intersection

$\mathrm{P}(A \cup B)$ = $\mathrm{P}(A)$ + $\mathrm{P}(B)$ – $\mathrm{P}(A \cap B)$

Ces formules de probabilités se visualisent à l’aide du diagramme de Venn qui également utilisé sur les ensembles dans le programme de maths de seconde:

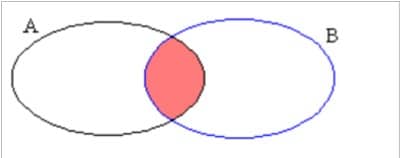
En foncée, la partie représentant l’intersection donc A∩B.

Exemple type sur les intersections et les unions pour illustrer :

Dans un collège de 450 élèves, on sait que 200 élèves prennent des cours particuliers de mathématiques, 150 font des cours particuliers de français et 50 font les deux. On choisit un élève au hasard, quelle est la probabilité qu’il fasse des cours particuliers en maths ou des cours particuliers en français ?

Réponse : la réponse n’est pas 400/450 !

200 élèves font des cours particuliers en maths, mais ils peuvent aussi faire des cours particuliers en français: aucune contre indication.

Sinon on aurait eu : « 200 élèves font uniquement des cours particuliers de maths»

Idem pour les 150 qui prennent des cours de français, certains prennent des cours de maths.

La seule chose dont on est sûr : 50 élèves prennent les deux matières donc :

200 – 50 = 150 élèves prennent uniquement des cours de maths
150 – 50 = 100 élèves prennent uniquement des cours de français

Nombre d’élèves qui font des cours de maths ou des cours de français :

Ceux qui font que des cours de maths + ceux qui font que des cours de français + ceux qui font les deux.

Soit : 150 +100 + 50 = 300 élèves. Et donc la probabilité cherchée vaut 300/450 soit 2/3.

COURS PARTICULIERS EN LIGNE

Nous avons sélectionné pour vous les meilleurs professeurs particuliers.

POUR ACCÉLÉRER MA PROGRESSION

Avis Google France ★★★★★ 4,9 sur 5

Arbre de probabilités cours

Il faut en faire quelques-uns pour que leur maniement devienne fluide et comprendre quand il faut les utiliser ou alors avoir de bons souvenirs du programme de maths de 1ère et Terminale.
Se souvenir :

Quand on veut tout un chemin (une intersection ∩), on multiplie les probabilités.
Si plusieurs chemins conviennent, on les additionne.

Exemple type pour illustrer les arbres en probabilités :

Un groupe est constitué aux trois quarts de garçons. On sait de plus que la moitié des garçons aime les maths contre 60% des filles. On choisit une personne du groupe au hasard, quelle est la probabilité qu’elle aime les maths ?

Réponse :

Quand on construit un arbre, il y a une forme de chronologie. Ici :

D’abord on est un garçon ou une fille,
puis on aime les maths ou pas

Le squelette de l’arbre est le suivant :

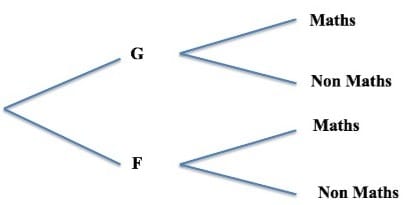
On le complète alors :

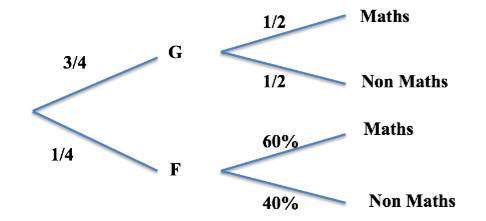
Pour les calculs, il faudra être cohérent : soit uniquement des fractions soit des pourcentages. On privilégie les fractions quasi exclusivement.

On cherche la probabilité que la personne aime les maths. Il y a 2 possibilités :

Soit cette personne aime les maths en étant un garçon (G∩M) soit $\dfrac {3}{4}$ $\times$ $\dfrac {1}{2}$
Soit cette personne aime les maths en étant une fille (F∩M) soit $\dfrac {1}{4}$ $\times$ $\dfrac {60}{100}$ (et $\dfrac {60}{100}$ = $\dfrac {6}{10}$ = $\dfrac {3}{5}$ )

Il y a donc deux chemins qui nous conviennent, on additionne « ces chemins », donc les probabilités trouvées, après les avoir simplifiées.

$\mathrm{P}(M)$ = $\dfrac {3}{4}$ $\times$ $\dfrac {1}{2}$ + $\dfrac {1}{4}$ $\times$ $\dfrac {3}{5}$

$\mathrm{P}(M)$ = $\dfrac {3}{8}$ + $\dfrac {3}{20}$ = $\dfrac {15}{40}$ + $\dfrac {6}{40}$ = $\dfrac {21}{40}$

Donc la probabilité que la personne aime les maths est de 21/40.

Dans la préparation du Tage Mage ou dans la préparation du Gmat ou même du Score IAE Message en vue d’entrer dans les meilleures écoles de commerce, les probabilités et le dénombrement occupent une bonne place dans les épreuves qui permettent de sélectionner les candidats. Cependant, d’autres cours sont également fondamentaux pour réussir le Tage Mage et plus particulièrement le sous-test 2, notamment :