Chapitres du sous-test 2 du Tage Mage
Le théorème de Thales : cours, formule et réciproque
Résumé de cours Exercices et corrigés
Le théorème de Thalès tout comme le théorème de Pythagore est une règle fondamentale de la géométrie classique. Le théorème de Thales est abordé la première fois au collège et doit donc être maîtrisé pour se préparer au brevet. Il est aussi demandé pour la prépa du Tage Mage et du Score IAE Message de connaitre et savoir appliquer le théorème de Thales et sa réciproque. Pour une meilleure maîtrise du théorème de Thales, nous vous invitons à suivre des cours particuliers de maths avec des professeurs agrégés et expérimentés.
Le théorème de Thales : formules de base
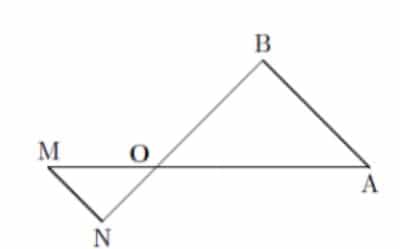
Sur les deux figures ci-dessous la droite (AB) est parallèle à la droite (MN)
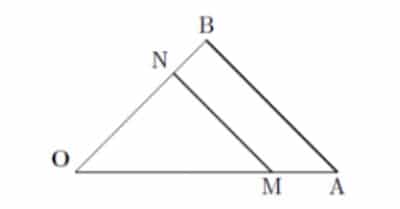
O est le point d’intersection en les deux droites sécantes (BN) et (AM)
Pour appliquer le théorème de Thales, plusieurs conditions sont nécessaires :
– Le point M est sur la droite (OA)
– Le point N est sur la droite (OB)
– les droites (MN) et (AB) sont parallèles : (MN) // (AB)
D’après le théorème de Thalès, on peut donc en déduire que :
$\dfrac{OM}{OA}$ = $\dfrac{ON}{OB}$ = $\dfrac{MN}{AB}$
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Exemple d’application du théorème de Thalès :
Sur la figure ci-dessous, les dimensions ne sont pas respectées.
Les droites (RS) et (LK) sont parallèles.
On donne :
LM = 6 cm, LK = 5 cm, KM = 8 cm et SM = 6 cm.
Calculer MR.
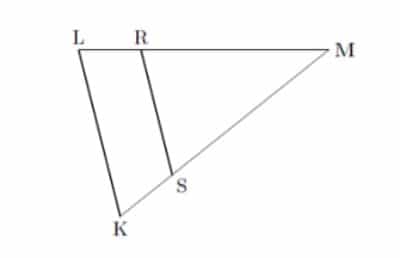
Calculons RM.
Le point R est sur la droite (ML)
Le point S est sur la droite (MK)
Les droites (RS) et (LK) sont parallèlles : (RS) // (LK)
D’après le théorème de Thalès,
$\dfrac{MR}{ML}$ = $\dfrac{MS}{MK}$ = $\dfrac{RS}{LK}$
D’où $\dfrac{MR}{ML}$ = $\dfrac{MS}{MK}$
D’où $\dfrac{MR}{6}$ = $\dfrac{6}{8}$
Donc 8 x MR = 6 x 6
Finalement MR = $\dfrac{36}{8}$ = $\dfrac{9}{2}$
Autre exemple d’application du théorème de Thales :
Sur la figure ci-dessous, les dimensions ne sont pas respectées.
Les droites (AB) et (CD) sont parallèles.
Les droites (AC) et (BD) sont sécantes en E.
On donne :
AB = 3 cm, BD = 9 cm, AC = 6 cm et BE = 5 cm.
Calculer CD.
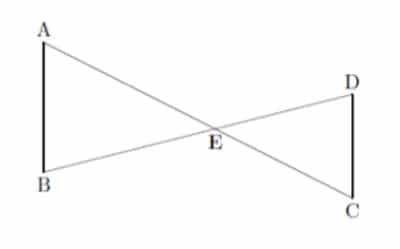
Calculons CD.
Le point C est sur la droite (EA)
Le point D est sur la droite (EB)
Les droites (CD) (AB) sont parallèles : (CD) // (AB)
D’après le théorème de Thalès,
$\dfrac{EC}{EA}$ = $\dfrac{ED}{EB}$ = $\dfrac{CD}{AB}$
D’où $\dfrac{ED}{EB}$ = $\dfrac{CD}{AB}$
D’où ED = BD – BE = 9 – 5 = 4 cm
Finalement : $\dfrac{4}{5}$ = $\dfrac{CD}{3}$
5 x CD = 4 x 3
Donc CD = $\dfrac{12}{5}$
COURS DE MATHS A DOMICILE
Les meilleurs profs de maths pour
réussir sa scolarité
En ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
La réciproque du théorème de Thalès
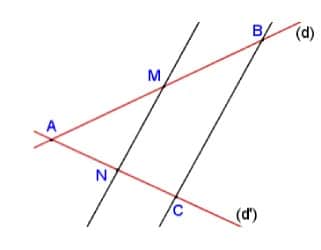
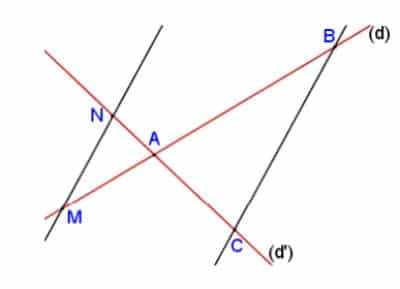
Soient (d) et (d’) deux droites sécantes en A.
Soient B et M deux points de la droite (d), distincts de A.
Soient C et N deux points de la droite (d’), distincts de A.
Si $\dfrac{AM}{AB}$ = $\dfrac{AN}{AC}$ et si les points A, B, M et les points A, C, N sont dans le même ordre, alors les droites (BC) et (MN) sont parallèles.
Exemple d’application de la réciproque du théorème de Thales :
On considère la figure ci-contre.
Démontrer que les droites (BD) et (EC) sont parallèles.
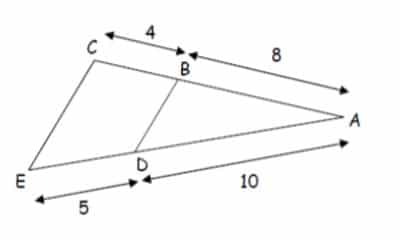
Comparons $\dfrac{AB}{AC}$ et $\dfrac{AD}{AE}$
$\dfrac{AB}{AC}$ = $\dfrac{8}{12}$ = $\dfrac{2}{3}$
$\dfrac{AD}{AE}$ = $\dfrac{10}{15}$ = $\dfrac{2}{3}$
Donc $\dfrac{AB}{AC}$ = $\dfrac{AD}{AE}$
Les droites (BC) et (DE) sont sécantes en A.
Comme $\dfrac{AB}{AC}$ = $\dfrac{AD}{AE}$ et puisque les points A, B et C sont alignés dans le même ordre que les points A, D et E d’après la réciproque du théorème de Thalès, les droites (BD) et (EC) sont parallèles.
Autre exemple d’application de la réciproque du théorème de Thalès :
Sur la figure ci-dessous, les points G, T et L sont alignés et les points F, T et P sont alignés.
Les droites (FG) et (LP) sont-elles parallèles ?
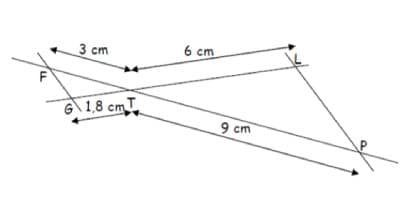
Comparons $\dfrac{TG}{TL}$ et $\dfrac{TF}{TP}$
$\dfrac{TG}{TL}$ = $\dfrac{1,8}{6}$ = $\dfrac{18}{60}$ = $\dfrac{3}{10}$
$\dfrac{TF}{TP}$ = $\dfrac{3}{9}$ = $\dfrac{1}{3}$
Or $\dfrac{3}{10}$ ≠ $\dfrac{1}{3}$ donc $\dfrac{TG}{TL}$ ≠ $\dfrac{TF}{TP}$.
De plus, les droites (FP) et (GL) sont sécantes en T.
Donc les droites (FG) et (LP) ne sont pas parallèles.
Ne relâchez pas vos efforts et assurez-vous de connaître sur le bout des doigts toutes les notions de mathématiques présentes dans le sous-test 2 Tage Mage, en utilisant nos cours en ligne du Tage Mage, dont en voici quelques-uns :

